批标准归一化（Batch Normalization）解析

1,背景

网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。

以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal Covariate Shift”，批标准归一化（Batch Normalization，BN）的提出，就是要解决在训练过程中，中间层数据分布发生改变的情况。

通过使用BN，每个神经元的激活变得（或多或少）高斯分布，即它通常中等活跃，有时有点活跃，罕见非常活跃。协变量偏移是不满足需要的，因为后面的层必须保持适应分布类型的变化（而不仅仅是新的分布参数，例如高斯分布的新均值和方差值）。

神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另外一方面，一旦每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
深度网络的训练是复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度

2，原理简介

Batch Normalization（简称BN）是对每一批数据进行归一化，对于训练中某一个batch的数据{x1,x2,…,xn}，注意这个数据是可以输入也可以是网络中间的某一层输出。在BN出现之前，我们的归一化操作一般都在数据输入层，对输入的数据进行求均值以及求方差做归一化，但是BN的出现打破了这一个规定，我们可以在网络中任意一层进行归一化处理，因为我们现在所用的优化方法大多都是min-batch SGD，所以我们的归一化操作就成为Batch Normalization。

批量归一化（Batch Normalization，BN）是神经网络的标准化方法/层，通常BN神经网络输入被归一化[0,1]或[-1,1]范围，或者意味着均值为0和方差等于1，即BN对网络的中间层执行白化。

如上图所示，BN步骤主要分为4步：
（1） 求每一个训练批次数据的均值
（2）求每一个训练批次数据的方差
（3）使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布。其中ε
是为了避免除数为0时所使用的微小正数。
（4）尺度变换和偏移（避免线性区）：将xi乘以γ调整数值大小，再加上β增加偏移后得到yi，这里的γ是尺度因子，β是平移因子。这一步是BN的精髓，由于归一化后的xi基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数：γ,β。 γ和β是在训练时网络自己学习得到的。

一个标准的归一化步骤就是减均值除方差，那这种归一化操作有什么作用呢？我们观察下图：

a中左图是没有经过任何处理的输入数据，曲线是sigmoid函数，如果数据在梯度很小的区域，那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后，数据就被移到中心区域如右图所示，有效避免分布数据偏移，使其远离导数饱和区。对于大多数激活函数而言，这个区域的梯度都是最大的或者是有梯度的（比如ReLU），这可以看做是一种对抗梯度消失的有效手段。对于一层如此，如果对于每一层数据都那么做的话，数据的分布总是在随着变化敏感的区域，相当于不用考虑数据分布变化了，这样训练起来更有效率。

那么为什么要有第4步，不是仅使用减均值除方差操作就能获得目的效果吗？思考一个问题，减均值除方差得到的分布是正态分布，我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢？不能，比如数据本身就很不对称，或者激活函数未必是对方差为1的数据最好的效果，比如Sigmoid激活函数，在-1~1之间的梯度变化不大，那么非线性变换的作用就不能很好的体现，换言之就是，减均值除方差操作后可能会削弱网络的性能！针对该情况，在前面三步之后加入第4步完成真正的batch normalization。

BN的本质就是利用学习优化，改变一下方差大小和均值位置，使得新的分布更切合数据的真实分布，保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差，那么经过batch normalization之后的数据和输入完全一样，当然一般的情况是不同的。

3，BP对神经网络的影响

3.1 激活函数

在所有情况下，BN都能显著提高训练速度，如果没有BN，使用Sigmoid激活函数会有严重的梯度消失问题。
如下图所示，激活函数sigmoid、tanh、relu在使用了BN后，准确度都有显著的提高（虚线是没有用BN的情况，实线是对应的使用BN的情况）
3.2 优化器

Adam是一个比较犀利的优化器，但是如果普通的优化器 ,比如随机梯度下降法，加上BN后，其效果堪比Adam。
ReLU +Adam≈ReLU+ SGD + BN
所以说，使用BN，优化器的选择不会产生显着差异。

3.3 批量大小

对于小批量（即4），BN会降低性能，所以要避免太小的批量，才能保证批归一化的效果。

3.4 数据不平衡

如果对于具有分布极不平衡的二分类测试任务（例如，99：1），BN破坏性能并不奇怪。也就是说，这种情况下不要使用BN。

3.5 梯度消失的问题

如下图所求，BN很好地解决了梯度消失问题，这是由前边说的减均值除方差保证的，把每一层的输出均值和方差规范化，将输出从饱和区拉倒了非饱和区（导数），很好的解决了梯度消失问题。下图中对于第二层与第一层的梯度变化，在没有使用BN时，sigmoid激活函数梯度消失5倍，使用BN时，梯度只消失33%；在使用BN时，relu激活函数梯度没有消失。

3.6 模型正则化

BN算法后，参数进行了归一化，不用太依赖drop out、L2正则化解决归 一化，采用BN算法后可以选择更小的L2正则约束参数，因为BN本身具有提高网络泛化能力的特性。

4,模型预测时均值和方差求解

对于预测阶段时所使用的均值和方差，其实也是来源于训练集。比如我们在模型训练时我们就记录下每个batch下的均值和方差，待训练完毕后，我们求整个训练样本的均值和方差期望值，作为我们进行预测时进行BN的的均值和方差：

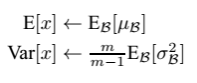
最后测试阶段，BN的使用公式就是：

关于BN的使用位置，在CNN中一般应作用与非线性激活函数之前，s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是：

其实因为偏置参数b经过BN层后其实是没有用的，最后也会被均值归一化，当然BN层后面还有个β参数作为偏置项，所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了：

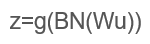
注意前面写的都是对于一般情况，对于卷积神经网络有些许不同。因为卷积神经网络的特征是对应到一整张特征响应图上的，所以做BN时也应以响应图为单位而不是按照各个维度。比如在某一层，batch大小为m，响应图大小为w×h，则做BN的数据量为m×w×h。

BN在深层神经网络的作用非常明显：若神经网络训练时遇到收敛速度较慢，或者“梯度爆炸”等无法训练的情况发生时都可以尝试用BN来解决。同时，常规使用情况下同样可以加入BN来加速模型训练，甚至提升模型精度。