二叉树经典例题

解决二叉树相关问题，常见的思路有两种，一是利用二叉树的遍历序列，二是利用递归，当然也可能是二者都有。

对称二叉树

判断一个二叉树是否关于root轴对称。

这道题看起来似乎可以用中序遍历解决，因为对称二叉树的中序序列一定是回文的。但是中序序列为回文的二叉树未必是对称的，比如上图中假如把两个叶子节点的值改为2，它的中序就是2,2,1,2,2，但是它并不对称。

这道题应该用递归来解决，不过注意如何比较左右子树

public class Solution {
    public bool IsSymmetric(TreeNode root) {
        if(root==null)
        return true;
        return mirror(root.left,root.right);
    }
    public bool mirror(TreeNode l,TreeNode r)
    {
        if(l==null&&r==null)
        return true;
        if((l!=null&&r==null)||(l==null&&r!=null)||l.val!=r.val)
        return false;
        return mirror(l.left,r.right)&&mirror(l.right,r.left);
    }
}

 从中序与（前）后序遍历序列构造二叉树

在前序和后序序列中，根节点的位置是确定的，而在根节点已知的情况下，就可以通过中序序列划分左右子树，再通过它们划分前序或后序中的左右子树，然后递归下去便可以得到整个二叉树了。

public class Solution {
    public TreeNode BuildTree(int[] inorder, int[] postorder) {
        TreeNode root=new TreeNode();
        root.val=postorder[postorder.Length-1];
        if(inorder.Length==1)
        return root;
        int i=0;
        while(inorder[i]!=root.val)
        i++;
        if(i!=0)
        {
            int[] leftin=copyArray(inorder,0,i-1);
            int[] leftpost=copyArray(postorder,0,i-1);
            root.left=BuildTree(leftin,leftpost);
        }
        if(i!=inorder.Length-1)
        {
            int[] rightin=copyArray(inorder,i+1,inorder.Length-1);
            int[] rightpost=copyArray(postorder,i,postorder.Length-2);
            root.right=BuildTree(rightin,rightpost);
        }
        return root;
    }
    public int[] copyArray(int[]nums,int start,int end)
    {
        int length=end-start+1;
        int[] newArray=new int[length];
        for(int i=0;i<length;i++)
        newArray[i]=nums[start+i];
        return newArray;
    }
}

填充每个节点的下一个右侧节点指针

 

 这道题很容易想到是利用bfs来解决，在每一层的节点都出队后两两相连。

public class Solution {
    public Node Connect(Node root) {
        if(root==null||(root.left==null&&root.right==null))
        return root;
        Queue q=new Queue();
        q.Enqueue(root);
        while(q.Count!=0)
        {
            int len=q.Count,i;
            Node[] nodes=new Node[len];
            for(i=0;i<len;i++)
            {
                nodes[i]=(Node)q.Dequeue();
                if(i>0)
                nodes[i-1].next=nodes[i];
            }
            for(i=0;i<len;i++)
            {
                if(nodes[i].left!=null)
                q.Enqueue(nodes[i].left);
                if(nodes[i].right!=null)
                q.Enqueue(nodes[i].right);
            }
        }
        return root;
    }
}

二叉树的最近公共祖先

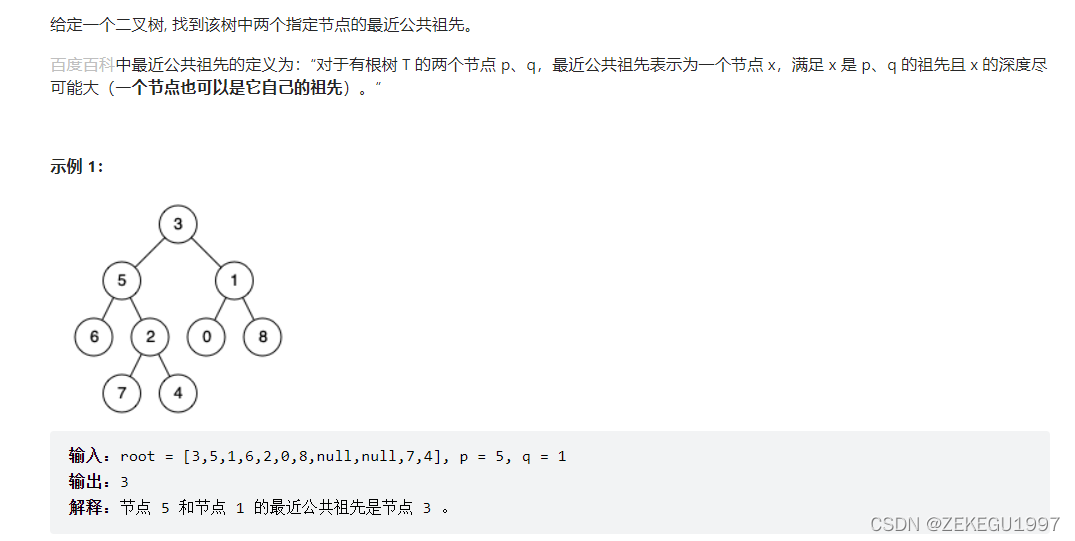
 这道题本质上是确定pq两个节点的位置，如果pq中一个是根节点或者它们分别属于左右子树，则公共祖先是根节点，否则就对它们所在的子树继续迭代。

确定pq位置的方法有两种，一种是递归搜索，还有一种是利用中序序列，下面代码为中序序列。

public class Solution {
    public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<int> order=new List<int>();
        order=inorder(root);
        int r=order.IndexOf(root.val),a=order.IndexOf(p.val),b=order.IndexOf(q.val);
        while(!(a==r||b==r||(a<r&&r<b)||(b<r&&r<a)))
        {
            if(a<r&&b<r)
            root=root.left;
            else
            root=root.right;
            r=order.IndexOf(root.val);
        }
        return root;
    }
    
    public List<int> inorder(TreeNode root)
    {
        List<int> a=new List<int>(),b=new List<int>(),c=new List<int>();
        if(root==null)
        return a;
        if(root.left!=null)
        b=inorder(root.left);
        a.AddRange(b);
        a.Add(root.val);
        if(root.right!=null)
        c=inorder(root.right);
        a.AddRange(c);
        return a;
    }
}

二叉树的序列化与反序列化

 这道题有两个部分，序列化和反序列化。按照LeetCode默认的格式，序列化的过程与bfs是很接近的，略有不同的是我们得到的是一个字符串，并且需要记录空的子节点。为了分隔不同的数字，我们在两个节点的值之间加上逗号，把空子节点记为‘#’。

有了序列化，就可以设计与之对应的反序列化了。反序列化中有一些难点，如何找到或者说确定父子节点，如何保存父子节点。序列化是按照bfs的顺序，自然反序列化也要按照层次的顺序，而在层次遍历中父子节点相隔可能比较远，而且由于存在空节点等，间隔难以确定。

所以一个办法是把上下两层的节点都保存下来，再进行一一配对。这里又有另一个问题：保存两层的节点用什么数据结构？备选的有三种：数组，队列，列表。在c#中无法直接获取数组中的元素个数（length 是初始化数组的长度），队列可以获得元素数量，但是不能直接用索引调用，所以最合适的是列表。

public class Codec {
    // Encodes a tree to a single string.
    public string serialize(TreeNode root) {
        if(root==null)
        return null;
        Queue q=new Queue();
        string bfs="";
        q.Enqueue(root);
        bfs+=root.val.ToString();
        bfs+=',';
        while(q.Count!=0)
        {
            int len=q.Count;
            for(int i=0;i<len;i++)
            {
                TreeNode t=new TreeNode(0);
                t=(TreeNode)q.Dequeue();
                if(t.left!=null)
                {
                    bfs+=t.left.val.ToString();
                    bfs+=',';
                    q.Enqueue(t.left);
                }
                else
                {bfs+='#';bfs+=',';}
                if(t.right!=null)
                {
                    bfs+=t.right.val.ToString();
                    bfs+=',';
                    q.Enqueue(t.right);
                }
                else
                {bfs+='#';bfs+=',';}
            }
        }
        bfs=bfs.Remove(bfs.Length-1);
        return bfs;
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(string data) {
        if(data==null)
        return null;
        List<TreeNode> tree= new List<TreeNode>();//父节点层
        string tempstr="";
        int i=0;
        while(data[i]!=',')
        {
            tempstr+=data[i];
            i++;
        }i++;
        TreeNode root = new TreeNode(0);
        root.val=Convert.ToInt32(tempstr);
        tree.Add(root);
        int len=0;
        while(i<data.Length)
        {
            len=tree.Count;
            List<TreeNode> newtree = new List<TreeNode>();//子节点层
            for(int j=0;j<2*len;j++)//2*len是子节点层最大可能的节点数
            {
            if(data[i]!='#')
            {
                tempstr="";
                while(data[i]!=',')
                {
                    tempstr+=data[i];
                    i++;
                }
                TreeNode temp = new TreeNode(0);
                temp.val=Convert.ToInt32(tempstr);//string转int
                newtree.Add(temp); 
                if(j%2==0)
                tree[j/2].left=temp;
                else
                tree[j/2].right=temp;
            }
            else
                i++;
            i++;
            }
            tree=newtree;
        }
        return root;
    }
}