图的存储结构——邻接矩阵实现

由于在图中，任何两个顶点之间都可能存在联系，所以无法在存储位置上反映数据元素之间的联系，因此图没有顺序存储结构。按图中顶点之间的联系，图的存储结构似乎采用多重链表表示比较恰当。但是若采用多重链表，则链表中结点的结构难以确定。如果结点中的指针数若按顶点度的最大值来设置，则会浪费空间。因为有很多顶点的度小于最大值：若顶点的指针数按每个顶点的度数来设置，则存储结构中会有很多顶点的结构不一致，给图的运算带来困难。因此，图的存储结构不宜采用多重链表。一般来说，图的存储结构应根据具体问题的要求来设计。常用的存储结构有邻接矩阵、邻接表、邻接多重表和十字链表。

7.2.1 邻接矩阵Adjacency Matrix

定义

若设图G=（V，E）是一个有n个顶点的图，则图的邻接矩阵是一个二维数组Arcs[n][n]，它的定义为：
arcs[i][j]=1，(i,j)∈E || <i,j>∈E ；
否则 arcs[i][j]=0.

1. 对于网络（或带权图） ，邻接矩阵定义如下；
   arcs[i][j]= W(i,j)，i≠j && (i,j)∈E || <i,j>∈E ;
   arcs[i][j]= ∞ ，i≠j && (i,j)不属于E || <i,j>不属于E；
   arcs[i][j]= 0 ，i=j.
2. 矩阵行列非零个数与度的关系：
   无向图某一行或者某一列的非零元素个数表示该行顶点的度数；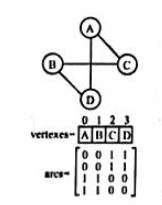
   有向图某一行的非零元素个数表示该行顶点的出度OutDdgree，某一列的非零元素个数表示该列顶点的入度InDegree。
   以下图为例，v1有到v2,v3的两个出度，因而第一行第2、3个元素是1，这一行非零元素有两个；v4到v1有一个入度，因而第一列第4个元素是1，这一列非零元素有一个。
   
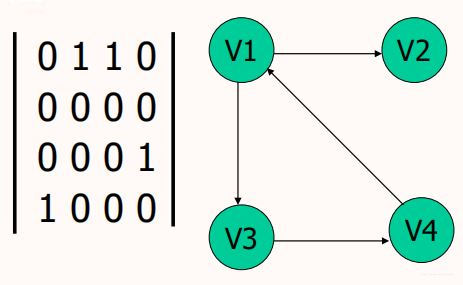
3. 无向图的邻接矩阵一定是对称的；有向图的邻接矩阵不一定对称。
4. 对于带权图而言，出入度不仅要考虑非零（i=j）还要考虑不等于 ∞（没有边的关联）；

无向图的邻接矩阵类模板

邻接矩阵类定义

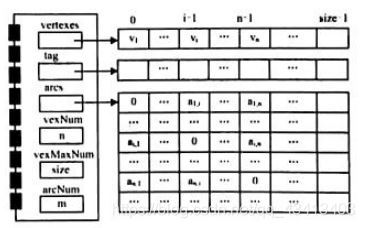
其中有一个数组vertexes，用以存放图中顶点的信息；还有一个作为邻接矩阵使用的二维数组arcs[ ][ ]，用以表示图中顶点之间的关系，其中矩阵元素个数取决于顶点个数，与边数无关；另外还定义了vexNum、vexMaxNum和arcNum三个数据成员，分别记录图中当前顶点数目、允许的顶点最大数目和边数：为了在图的遍历等算法中记录顶点是否访问，在此定义了一个标志数组tag，需要时用以记录顶点的访问状况。

//自定义类型
enum Status {
   
   SUCCESS, FAIL, UNDER_FLOW, OVER_FLOW,RANGE_ERROR, DUPLICATE_ERROR,
	NOT_PRESENT, ENTRY_INSERTED, ENTRY_FOUND, VISITED, UNVISITED};

// 无向图的邻接矩阵类
template <class ElemType>
class AdjMatrixUndirGraph 
{
   
   
protected:
// 邻接矩阵的数据成员:
	int vexNum, vexMaxNum, arcNum;			// 顶点数目、允许的顶点最大数目和边数
	int **arcs;							    // 存放边信息邻接矩阵
	ElemType *vertexes;						// 存放顶点信息的数组 
	mutable Status *tag;					// 标志数组

public:
// 邻接矩阵类型的方法声明:
	AdjMatrixUndirGraph(ElemType es[], int vertexNum, int vertexMaxNum = DEFAULT_SIZE);	
		// 以数组es[]为顶点,顶点个数为vertexNum,允许的顶点最大数目为vertexMaxNum,边数为0的无向图
	AdjMatrixUndirGraph(int vertexMaxNum = DEFAULT_SIZE);	
		// 构造允许的顶点最大数目为vertexMaxNum,边数为0的无向图
	~AdjMatrixUndirGraph();					// 析构函数
	void Clear();			              // 清空图			 
	bool IsEmpty();                 // 判断无向图是否为空 
	int GetOrder(ElemType &d) const;// 求顶点的序号	
	Status GetElem(int v, ElemType &d) const;// 求顶点的元素值	
	Status SetElem(int v, const ElemType &d);// 设置顶点的元素值
	int GetVexNum() const;					// 返回顶点个数			 
	int GetArcNum() const;					// 返回边数			 
	int FirstAdjVex(int v) const;		// 返回顶点v的第一个邻接点			 
	int NextAdjVex(int v1, int v2) const;		 // 返回顶点v1的相对于v2的下一个邻接点			 
	void InsertVex(const ElemType &d);			 // 插入元素值为d的顶点		 
	void InsertArc(int v1, int v2);			     // 插入顶点为v1和v2的边			 
	void DeleteVex(const ElemType &d);			 // 删除元素值为d的顶点			 
	void DeleteArc(int v1, int v2);			     // 删除顶点为v1和v2的边			 
	Status GetTag(int v) const;			         // 返回顶点v的标志		 
	void SetTag(int v, Status val) const;	   // 设置顶点v的标志为val		 
	AdjMatrixUndirGraph(const AdjMatrixUndirGraph<ElemType> &g);	// 复制构造函数
	AdjMatrixUndirGraph<ElemType> &operator =(const AdjMatrixUndirGraph<ElemType> &g); 
		// 赋值语句重载
  void Display();	                         // 显示邻接矩阵无向图
};

类的实现

1. 函数的实现介绍
   1.1 构造函数1
   根据参数 vertexMaxNum指定的允许顶点最大数目构造一个空的无向图。
   template<class ElemType> AdjMatrixundirGraph<ElemType>::AdjMatrixundirGraph(int vertexMaxNum);
   1.2 构造函数2
   根据es[ ]数组中的数据元素，构造顶点个数为vertexNum、允许的顶点最大数目为vertexMaxNum、边数为0的无向图。
   template <class ElemType> AdjMatrixUndirGraph<ElemType>::AdjMatrixUndirGraph(ElemType es[]，int vertexNum,int vertexMaxNum);
   1.3 求第一个邻接点序号
   求顶点v的第一个邻接点序号。如果顶点v不存在，则抛出异常：如果顶点v没有邻接顶点，则返回-1。
   template <class ElemType> int AdjMatrixundirGraph<ElemType>::FirstAdjVex(int v) const;
   1.4 求下一个邻接点序号
   求顶点vl的相对于v2的下一个邻接点序号。如果顶点vl、v2不存在，则抛出异常；如果在顶点v2后顶点vl没有邻接顶点，则返回-1。
   template <class ElemType> int AdjMatrixUndirGraph<ElemType>::NextAdjVex(int v1，int v2) const;
   1.5 插入顶点
   如果图的顶点数已经达到允许的最大值，则抛出异常；否则把顶点d插入顶点数组的最后。
   template <class ElemType> void AdjMatrixUndirGraph<Elemrype>::InsertVex(const ElemType &d);
   1.6 插入边
   如果顶点vl、v2不存在，或vl、v2相等则抛出异常；否则，如果顶点v1、v2之间原来不存在边，则在两个顶点之间插入边。
   template <class Elemfype> void AdjMatrixundirGraph<ElemType>::InsertArc(int v1，int v2);
   1.7 删除顶点
   在图的邻接矩阵中删除顶点相对来说要复杂一点。先查找要删除的顶点d是否存在，如果顶点d不存在则抛出异常；否则先删除依附于顶点d的边，接着考虑删除项点d。如果被删除的是顶点表中最后一个顶点，则只要把顶点数减一就完成了顶点的删除；否则把顶点表中最后一个顶点的信息移到顶点d的位置，并在邻接矩阵中把最后一行和最后一列的信息移到顶点d对应的行和列，最后再把顶点数减一完成顶点的删除。
   
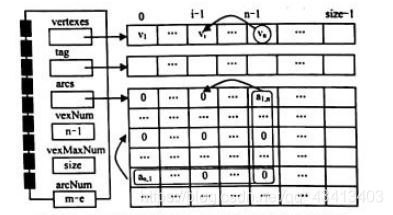
   template <class ElemType> void AdjMatrixundirGraph<ElemType>::DeleteVex(const ElemType &d);
   1.8删除边
   如果顶点v1、v2不存在，或v1、v2相等则抛出异常；否则如果顶点v1、v2之间原来存在边，则删除两个顶点之间的边。
   template <class ElemType>
   void AdjMatrixundirGraph<ElemType>::DeleteArc(int v1，int v2);
2. 函数的实现代码

// 无向图的邻接矩阵类的实现部分
template <class ElemType>
AdjMatrixUndirGraph<ElemType>::AdjMatrixUndirGraph(ElemType es[], int vertexNum, int vertexMaxNum)
// 操作结果：构造数据元素为es[],顶点个数为vertexNum,允许的顶点最大数目为vertexMaxNum,边数为0的无向图

{
   
   
	if (vertexMaxNum < 0)
    	throw Error("允许的顶点最大数目不能为负!");        // 抛出异常

	if (vertexMaxNum < vertexNum)
    	throw Error("顶点数目不能大于允许的顶点最大数目!");// 抛出异常