查找——索引顺序表和倒排表

最新推荐文章于 2021-08-01 20:24:00 发布

原创最新推荐文章于 2021-08-01 20:24:00 发布 · 6.1k 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

数据结构专栏收录该内容

37 篇文章

订阅专栏

本文详细介绍了索引顺序表和倒排表，包括完全索引和二级索引的概念，以及链式和单元式倒排索引表的特点。在完全索引中，二级索引查找成功时的平均查找长度与子表中索引项个数有关。倒排表则常用于针对数据元素的次关键字建立查找，以提高搜索效率。

查找

8.3 索引顺序表和倒排表

8.3 索引顺序表和倒排表

当数据表中的数据元素个数n很大时，如果用顺序查找结构，则查找效率极低。如果采用有序表存储形式的折半查找，则为了维持数据表的有序性，时间开销很大；而且，当数据表很大时，计算机内存的容量可能不够。这时可采用索引方法来实现存储和查找。

8.3.1 索引顺序表

索引顺序表一般由主表和索引表两个部分组成，两者均采用顺序存储结构。
主表中存放数据元素的全部信息，索引表中存放数据元素的主键字和索引信息。

（1）完全索引

在图8-3所示的学生信息表的例子中，一个索引项对应数据表中一个数据元素，这时的索引结构叫作稠密索引也称完全索引。稠密索引结构适用于当数据元素在外存中按加入次序存放而不是按关键字有序存放的情形。
完全索引表中关键字分块有序存放，即把所有n个索引项分为m个块（子表），井且后一个子表中所有的关键字均大于前一个子表中所有的关键字，而在同一子表中所有关键字的次序任意。分块有序，索引按照关键字的大小建立，可知大于某个值或者小于某个值可以到哪个块里面去查找。经典的分块查找要求块间有序、块内也有序，如果块与块无序就无法建立索引。
分块查找的具体实现
转载自：https://www.cnblogs.com/ciyeer/p/9067048.html

#include <stdio.h>
#include <stdlib.h>
struct index { 　　//定义块的结构
　　int key;
　　int start;
} newIndex[3];  //定义结构体数组
int search(int key, int a[]);
int cmp(const void *a,const void* b){
　　return (*(struct index*)a).key>(*(struct index*)b).key?1:-1;
}
int main(){
　　int i, j=-1, k, key;
　　int a[] = {33,42,44,38,24,48, 22,12,13,8,9,20, 60,58,74,49,86,53};
　　//确认模块的起始值和最大值
　　for (i=0; i<3; i++) 　　{
　　　　newIndex[i].start = j+1; //确定每个块范围的起始值
　　　　j += 6;
　　　　for (int k=newIndex[i].start; k<=j; k++) 　　　　{
　　　　　　if (newIndex[i].key<a[k]) 　　　　　　{
　　　　　　　　newIndex[i].key = a[k];
　　　　　　}
　　　　}
　　}
　　//对结构体按照 key 值进行排序
　　qsort(newIndex,3, sizeof(newIndex[0]), cmp);
　　//输入要查询的数，并调用函数进行查找
　　printf("请输入您想要查找的数：\n");
　　scanf("%d", &key);
　　k = search(key, a);
　　//输出查找的结果
　　if (k>0) 　　{
　　　　printf("查找成功！您要找的数在数组中的位置是：%d\n",k+1);
　　}　　else　　{
　　　　printf("查找失败！您要找的数不在数组中。\n");
　　}
　　return 0;
}
int search(int key, int a[]){
　　int i, startValue;
　　i = 0;
　　while (i<3 && key>newIndex[i].key) 　　{ 　　　　// 确定在哪个块中，遍历每个块，确定key在哪个块中
　　　　i++;
　　}
　　if (i>=3) 　　{ 　　　　//大于分得的块数，则返回0
　　　　return -1;
　　}
　　startValue = newIndex[i].start; //startValue等于块范围的起始值
　　while (startValue <= startValue+5 && a[startValue]!=key)
　　{
　　　　startValue++;
　　}
　　if (startValue>startValue+5) 　　{ 　　　　//如果大于块范围的结束值，则说明没有要查找的数
　　　　return -1;
　　}
　　return startValue;
}
运行结果：

请输入您想要查找的数：
22
查找成功！您要找的数在数组中的位置是：7

但是索引查找，块间有序，块内可以无序。查找过程是：
首先根据索引查到块，然后如果块内有序就可以二分查找，如果无序就只能顺序查找。如下图，要查找38：

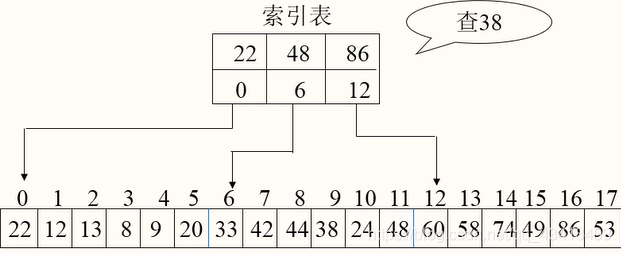
现在索引表看，38>22，而38<48，得到这个块的首地址6，直接找到6号位，（块内可以无序）并且从6号位开始顺序查找，直到9号位也是38，查找成功。

（2）二级索引

当完全索引表中关键字分块有序存放时，可以为完全索引表建立一个二级索引表，在二级索引表中一个索引项对应完全索引表中的一个子表，它记录了相应子表中最大关键字以及该子表在数据区中的起始位置，这种索引被称为二级索引，如图 8-4所示。
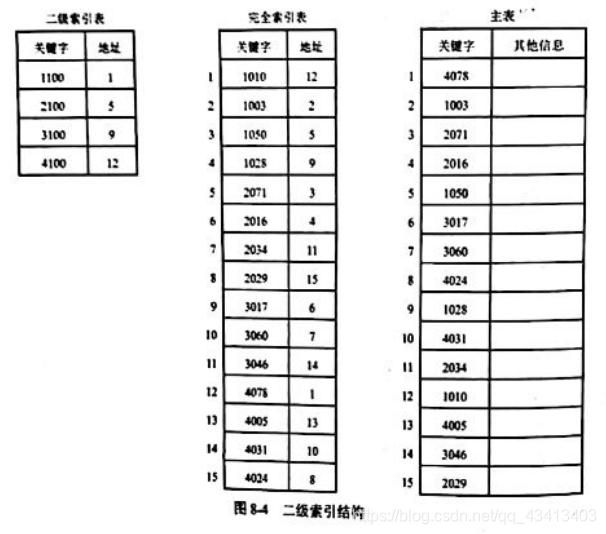
在这里插入图片描述

对二级索引结构进行查找时，一般分为二次查找。其过程是：
先在二级索引表中按给定值k进行查找，以确定待查子表的序号i，使得序号为i-1的子表中的最大关键字<k<=序号为i的子表中的最大关键字。然后再在第i个子表中给定值查找关健字等于k的索引项。如果找到关键字等于k的索引项，则可以根据索引项内的地址直接从外存中读取相应的数据元素；否则表示查找失败。
二级索引表是按关键字有序的，且长度一般不太大，可以用折半查找，也可以顺序查找。
二级索引查找平均查找长度：
（1）查找成功
ASL(IndexSeq)=ASL(Index)+ASL(SubList)
其中，ASL(Index)是在二级索引表中查找成功的平均查找长度，ASL(SubList)是在子表内查找成功的平均查找长度。
设完全索引表的长度为n，分成均等的m个子表，每个子表中有k个对象，则m=⌈n/k⌉（向上取整）。
在等概率的情况下，每个子表的查找概率为1/m，子表内各对象的查找概率为1/k。
①若二级索引表和子表都用顺序查找，则二级索引查找成功时的平均查找长度为：
ASL(IndexSeq)=(n+k²)/(2k)+1
由此可见，二级索引查找的平均查找长度不仅与完全表索引表的长度n有关，而且与每个子表中所含的索引项个数k有关。那么，在给定n的情况下，当k=n^1/2时，ASL(IndexSeq)取极小值n^1/2+1。
②若对二级索引表采用折半查找、对子表用顺序查找，则二级索引查找成功时的平均查找长度为：
ASL(IndexSeq)=ASL(Index)+ASL(SubList)~log2(1+n/k)+k/2

结论

查找方法比较

n个元素	顺序查找	折半查找	分块查找
ASL	最大	最小	两者之间；顺序查找+顺序查找ASL=(n+k²)/(2k)+1；折半查找+顺序查找ASL~log2(1+n/k)+k/2
表结构	有序表、无序表	有序表	分块有序表
存储结构	顺序存储结构、线性链表	顺序存储结构	顺序存储结构、线性链表（块可以链式存储，但是要知道块的首地址）

8.3.2 倒排表

对包含有大量数据元素的数据表或文件进行查找时，最常用的方法是针对数据元素的主关键字建立索引表，用主关键字建立的索引叫作主索引，主索引表的每个索引项给出数据元素的关键字及其在数据表或文件中的存放地址。但在实际应用中有时需要针对其他属性进行查找。
因此，除主关健字外，可以把一些在查找时经常用到的属性设定为次关键字，并以每一个属性作为次关键字建立次索引表，称之为倒排索引表。
倒排索引表有链式和单元式两种结构。

（1）链式倒排索引表

在链式倒排索引表中，列出了作为次关键字属性的所有取值，并对每一个取值建立有序链表，把所有具有相同属性值的主关键字按其递增的顺序或按其在主索引表中的存储地址巡增的顺序链接在一起。
因此，链式倒排索引表包拓三个部分：次关键字、链表长度和有序链表。
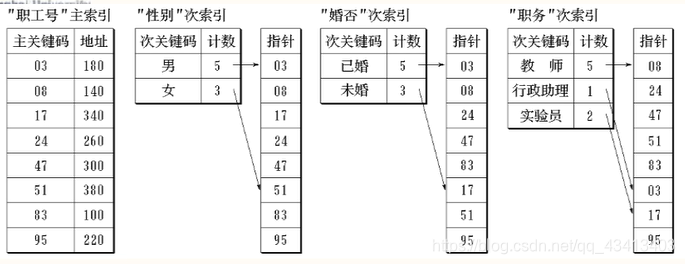
由于主关键宁技大小依次有序存放上表的长度确定，因此在静态链表中可省去指针域。
在链式倒排索引表中各个属性链表的长度大小不一，管理起来比较困难。

（2）单元倒排索引表

为此引入单元式倒排索引表，在单元式倒排表中，索引项中不存放对象的存储地址，存放该对象所在硬件区域的标识。硬件区域可以是磁盘柱面、磁道或一个页块，以一次I/O操作能存取的存储空间作为硬件区域为最好。为使索引空间最小，在索引中标识这个硬件区域时可以使用一个能转换成地址的二进制数，整个次索引形成一个（二进制数的）位矩阵。
因此，在单元式例排索引表的各个索引项中存放表示各外存区域是否存有相应数据元素的标识（以0或1表示）。于是，整个单元式倒排索引表将形成一个（二进制数的）位矩阵。
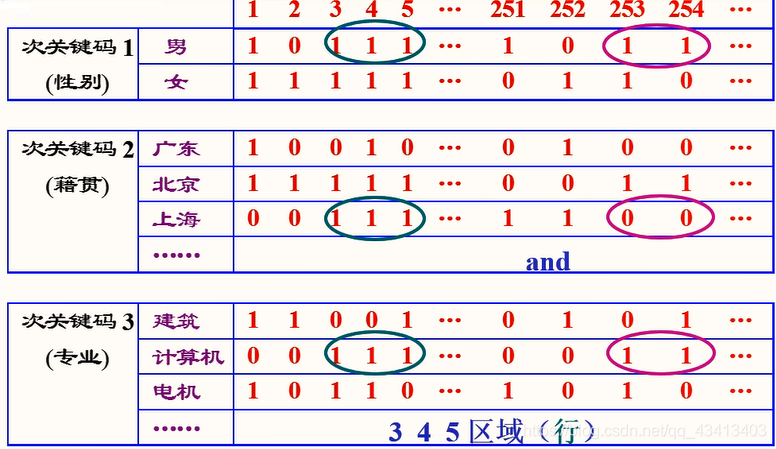
查找时，将相关索引项的二进制位串行进行按位“与”运算，求得所查数据元素在外存区域的区号。
例如，求计算机系的上海籍男生：

特点

倒排的优缺点和正排的优缺点整好相反。
所有正排的【优点】易维护；【缺点】搜索的耗时太长。
倒排【缺点】在构建索引的时候较为耗时且维护成本较高；【优点】搜索耗时短（在处理复杂的多关键字查询时，可在倒排表中先完成查询的交、并等逻辑运算，得到结果后再对记录进行存取。这样不必对每个记录随机存取，把对记录的查询转换为地址集合的运算，从而提高查找速度）。