编程题-子数组最大平均数

题目：

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

任何误差小于 10-5 的答案都将被视为正确答案。

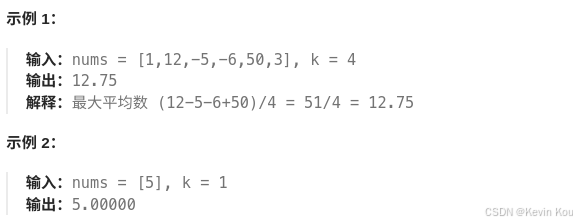
解法一（双层for循环-超时）：

双层循环体结构，从0一直遍历到尾部，再每次遍历过程内再计算遍历k个元素的和，这种两层循环在编程时大都会超时，因此不给予采用，仅作为与第二种方法的对比参考，如下代码：

class Solution {
public:
    double findMaxAverage(vector<int>& nums, int k) {
        int left = 0;
        int right = k;
        int length = nums.size();
        double max = -10000;
        double sum =0;
        while(right<length+1){
            for(int i=left; i<right;i++){
                sum+=nums[i];
            }
            if(max<(sum/k)){
                max = (sum/k);
            }
            left++;
            right++;
            sum=0;
        }
        return max;
    }
};

解法二（一次循环遍历）：

利用滑动窗口的思想替代双层for循环中的内层循环体，具体来说，再第二层循环体中是从0~k个元素重新相加的，但是当用滑动窗口的思想时，即为前一个sum值，加入第一层循环中前一个元素，再加上第一层循环中后一个元素，即为当前第二层循环体中sum元素的和。无需再写一层循环体来重新计算k个元素的和了，如下为笔者代码：

//降低时间复杂度版本
class Solution {
public:
    double findMaxAverage(vector<int>& nums, int k) {
        int left = 0;
        int length = nums.size();
        //其中，max初始值为赋值了一个尽可能大的值，作为负无穷值
        double max = -10000;
        double sum =0;
        //前计算初始时的k个元素值的和
        for(int i=0; i<k;i++){
            sum+=nums[i];
        }
        max = sum/k;
        //一次遍历元素，用sum = sum-nums[left]+nums[left+k];滑动窗口的思想，代替第二层循环体编写
        while(left<length-k){
            sum = sum-nums[left]+nums[left+k];
            if(max<(sum/k)){
                max = (sum/k);
            }
            left++;
        }
        return max;
    }
};

笔者小记：int、float、double数值类型赋值初始正无穷或负无穷值时，可以用尽可能大或小的数值进行替代，进而代替正无穷或负无穷，例如double max=-10000000;(即为max初始值为负无穷)。

除此之外，用用sum = sum-nums[left]+nums[left+k];滑动窗口的思想可以代替第二层循环体的编写，减少代码时间复杂度，在代码实现时要尽可能一次循环遍历解决问题，用其他方式替代第二层循环体的编写。