编程题-二叉树的层平均值

最新推荐文章于 2025-12-15 22:32:00 发布

原创最新推荐文章于 2025-12-15 22:32:00 发布 · 533 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #二叉树 #数据结构

题目：

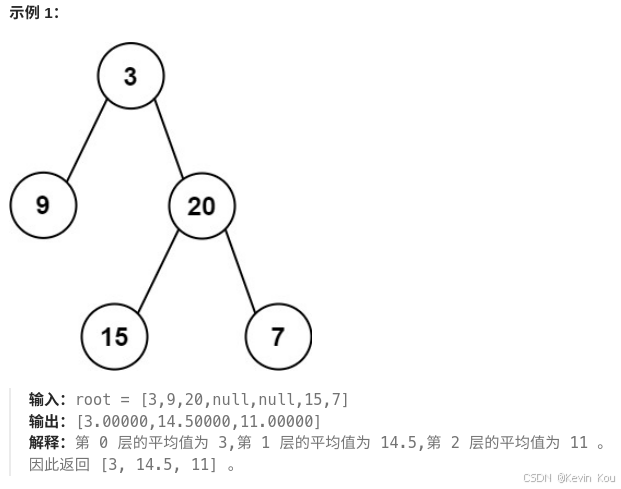
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 $10^{-5}$ 以内的答案可以被接受。

解题一（广度优先搜索）：

从根节点开始搜索，每一轮遍历同一层的全部节点，计算该层的节点数以及该层的节点值之和，然后计算该层的平均值。使用队列存储待访问节点，只要确保在每一轮遍历时，队列中的节点是同一层的全部节点即可。

初始时将根节点加入到队列中，然后每一轮遍历时，将队列中的节点全部取出，计算这些节点的数量以及它们的节点值之和，并计算这些节点的平均值，然后将这些节点的全部非空子节点加入队列，重复上述操作直到队列为空，遍历结束。如下为笔者的代码：

class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        queue<TreeNode*> Queue1;
        queue<TreeNode*> Queue2;
        vector<double> result;
        if(root==nullptr){
            return result;
        }
        Queue1.push(root);
        double sum=0;
        int a=0;
        while(!Queue1.empty() or !Queue2.empty()){
            TreeNode* root1 = Queue1.front();
            if(root1->left!=nullptr){
                Queue2.push(root1->left);
            }
            if(root1->right!=nullptr){
                Queue2.push(root1->right);
            }
            sum+=root1->val;
            a+=1;
            Queue1.pop();          
            if(Queue1.empty()){
                result.push_back((sum/a));
                sum=0;
                a=0;
                Queue1 = Queue2;
                while (!Queue2.empty()) {
                    Queue2.pop();
                }
            }
        }
        return result;
    }
};

解法二（深度优先搜索）：

使用深度优先搜索计算二叉树的层平均值，需要维护两个数组，counts用于存储二叉树的每一层的节点数，sums用于存储二叉树的每一层的节点值之和。搜索过程中需要记录当前节点所在的层，如果访问到的节点在第i层，则将counts[i]的值加1，并将该节点的值添加到sum[i]中。

在遍历结束后，第i层的平均值即为sums[i]/counts[i]。如下代码为：

class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        
        auto counts = vector<int>();
        auto sums = vector<double>();
        //初始时，root为根节点，0为根节点的层数
        dfs(root, 0, counts, sums);
        auto averages = vector<double>();
        int size = sums.size();
        //全部遍历完之后，再统一依次计算每一层的所有元素平均值
        for (int i = 0; i < size; i++) {
            averages.push_back(sums[i] / counts[i]);
        }
        return averages;
    }
    //深度优先搜索遍历二叉树的所有节点，嵌套函数的方法，dfs()函数中仍有dfs()函数，进行嵌套，counts和sums作为引用值，在执行嵌套函数中进行重复修改和赋值。
    void dfs(TreeNode* root, int level, vector<int> &counts, vector<double> &sums)                             
    {    
        if (root == nullptr) {
            return;
        }
        if (level < sums.size()) {
            sums[level] += root->val;
            counts[level] += 1;
        } else {
            sums.push_back(1.0 * root->val);
            counts.push_back(1);
        }
        dfs(root->left, level + 1, counts, sums);
        dfs(root->right, level + 1, counts, sums);
    }
};

笔者小记：vector(double) result;作为容器的定义，可以充当一维数组存储的数据结构，例如result[0],result[1]更实时灵活的处理每层树的平均值。dfs()函数内嵌套函数dsf()的利用可以反复的调用，类似与“递归”相同的操作，以及&counts, &sums引用的利用也可以在遍历树的过程中实时的修改和赋值。在后续代码编写中，可以更好的利用这些操作更快速的写出简洁漂亮的代码。