2024年最新5种智能算法优化BP神经网络
懒人救星版Matlab代码
BKA_BP 2024 黑翅鸢算法优化BP神经网络数据回归预测
HO_BP 2024 河马算法优化BP神经网络数据回归预测
GOOSE_BP 2024 鹅算法优化BP神经网络数据回归预测
NRBO_BP 2024 牛顿-拉夫逊优化BP神经网络数据回归预测
CPO_BP 2024 豪冠猪算法优化BP神经网络数据回归预测
整体运行效果对比图:
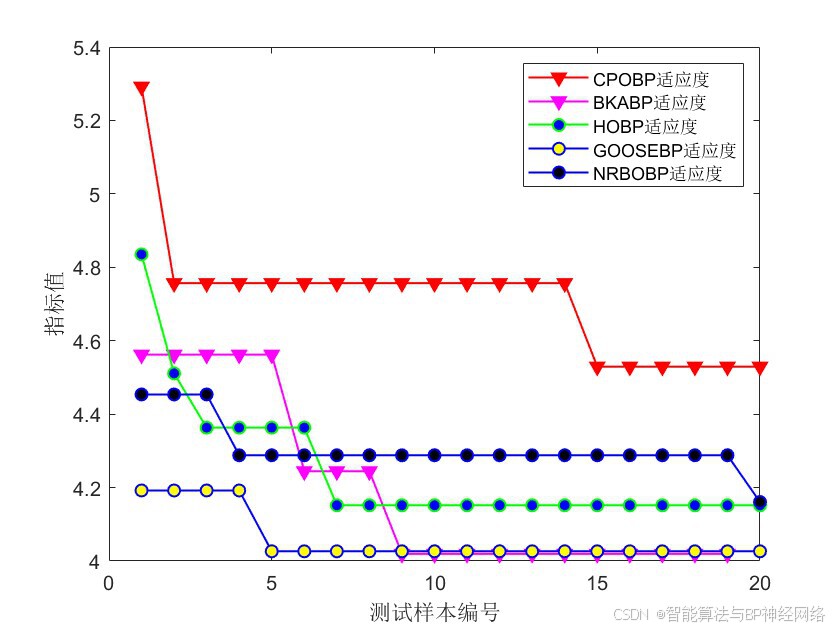




误差指标对比图:


懒人救星版:
1.任意多输入多输出(包括单输出)都可以用
4输入2输出.xlsx 4输入3输出.xlsx 5输入3输出.xlsx
2.加入数据拟合散点图
3.全新自适应作图,自适应对比求误差,自适应对输入输出进行归一化
数据特点:(多元化的数据)
包含0-1数据、大于1的数据和极大的数据(10的8次方)
改动代码处不超过4处:

数据集(三套:4输入2输出+4输入3输出+5输入3输出):
数据集一:

数据集二:
数据集三:

单一算法运行效果截图:(以2024河马算法优化BP为例)


五种算法对比效果:


CPO(冠豪猪算法)
原理:
CPO模拟了冠豪猪的各种防御行为。冠豪猪的四种防御策略是视觉、声音、气味和身体攻击。这些策略从最不激进到最激进排序。在CPO中,我们可以可视化搜索空间,四个不同的区域模拟了防御CP区域。第一个区域(A),CP远离捕食者,代表第一个防御区域,用于实施第一个防御策略。第二区域(B)代表第二防御区域,用于在捕食者不害怕第一防御机制并向捕食者移动的情况下实施第二防御策略。第三区域(C)代表第三防御区,用于实施第三防御策略,当捕食者不害怕第二和第三防御机制,仍向CP移动时,该策略被激活。最后一个区域(D)代表最后一个防御区域,用于实施最后一个防守策略。在最后一个区域,在之前的所有防御机制失效后,CP会攻击捕食者,使其失去能力,甚至杀死它们以保护自己。
一、种群初始化
与其他基于元启发式群体的算法类似,CPO从初始个体集(候选解决方案)开始搜索过程:

其中N表示个体数量(种群大小N),Xi是搜索空间中的第i个候选解,L和U分别是搜索范围的下限和上限,r是在0和1之间随机数
二、循环种群减少技术
循环种群减少技术(CPR),除了加快收敛速度外,还可以保持种群多样性。这种策略模拟了这样一种想法,即并非所有CP都激活防御机制,而是只有那些受到威胁的CP才激活防御机制。因此,在该策略中,在优化过程中从种群中获得一些CP,以加快收敛速度,并将它们重新引入种群中,从而提高多样性,避免陷入局部极小值;该循环基于循环变量T,以确定优化过程中执行该过程的次数。
N=Nmin+N-Nmin×(1-(t%TmaxTTmaxT ))
))
其中,T是确定循环数的变量,t是当前函数评估,Tmax是函数评估的最大数量,%表示余数或模运算符,Nmin是新生成的种群中个体的最小数量,因此种群大小不能小于Nmin。随着当前函数评估次数的增加,人口规模逐渐减少,甚至达到40人。这表示第一个循环。之后,种群规模再次最大化,然后逐渐减小,甚至达到优化过程的终点。这表示第二个也是最后一个周期,因为T被设置为2。由此可以看出,种群规模先是最大化,然后逐渐缩小,甚至达到Nmin。
三、勘探阶段
(1)第一防御策略
当CP意识到捕食者时,它开始举起并扇动羽毛笔,给人一种更深的印象。因此,捕食者有两种选择,要么向它移动,要么远离它。在第一种选择中,由于捕食者向CP移动,捕食者与CP之间的距离减小。这种选择鼓励探索捕食者与CP间的区域,以加快收敛速度。相反,在第二种选择中,捕食者和CP之间的距离最大化,因为捕食者选择离开。此选项鼓励探索遥远的地区,以确定未访问的地区,这可能涉及所需的解决方案。使用正态分布来生成随机值,以数学方式模拟这些选项。如果这些随机值小于1或大于−1,则鼓励向CP靠近。否则,捕食者将远离CP。通常,这种行为在数学上模拟如下:
Xit+1=Xit+τ1×2×τ2×Xcpt-yit
其中xtCP是评估函数t的最佳解,yti是在当前CP和从种群中随机选择的CP之间生成的向量,用于表示捕食者在迭代t时的位置,τ1是基于正态分布的随机数,τ2是区间[0,1]中的随机值。生成yti的数学公式如下所示:
yit=xit+xrt2
其中r是[1,N]之间的随机数。
(2)第二防御策略
在这种策略中,CP使用声音方法制造噪音并威胁捕食者。当捕食者靠近豪猪时,豪猪的声音会变得更大。为了从数学上模拟这种行为,提出了以下公式:

其中r1和r2是[1,N]之间的两个随机整数,τ3是0和1之间生成的随机值。
四、开发阶段
(1)第三防御策略
在这种策略中,CP会分泌恶臭,并在其周围区域传播,以防止捕食者靠近它。为了从数学上模拟这种行为,提出了以下公式:
xit+1=1-U1×xit×xr1t+Sit×xr2t-xr3t-τ3×δ×γt×Sit
其中r3是[1,N]之间的随机数,δ是用于控制搜索方向的参数,并使用等式(8)定义。xti是迭代t时第i个个体的位置,γt是使用等式(9)定义的防御因子。τ3是区间[0,1]内的随机值,Sti是使用(10)等式定义的气味扩散因子。如下所示:

其中,f(xit)表示迭代t时第i个个体的目标函数值,ε是避免被零除的小值,rand是包括在0和1之间随机生成的数值的矢量,rand是包括在1和0之间随机生成数字的变量,N是总体大小,t是当前迭代的次数,tmax是最大迭代次数。U1矢量用于模拟该策略中可能出现的三种情况:
(1)当U1 等于0,CP将停止气味扩散,因为捕食者会因为害怕CP而停止移动,因此捕食者与CP之间的距离保持不变;
(2)当U1等于1时,由于捕食者在附近,CP会显著散发气味;
(3) 当U1是0和1的组合,捕食者与CP保持安全距离,因此,没有必要广泛释放其气味。
(2)第四防御策略
最后一种策略是物理攻击。当捕食者离它很近并用短而厚的羽毛攻击它时,CP会采取物理攻击。在物理攻击过程中,两个物体强烈融合,代表一维的非弹性碰撞。为了用数学公式表达其物理攻击行为,提出了以下公式:

其中xtCP是获得的最佳解,表示xtiCP在迭代t时第i个个体的位置,表示该位置的捕食者,α是稍后在参数设置部分讨论的收敛速度因子,τ4是区间[0,1]内的随机值,Fti是影响第i个捕食者的CP的平均力。它由非弹性碰撞定律提供并由公式定义:

其中mi是迭代t时第i个个体(捕食者)的质量,f(‧)表示目标函数,vi(t+1)是第i个个体在下一次迭代t+1时的最终速度,并基于从当前总体中选择随机解进行分配,vti是迭代t时第i个个体的初始速度,Δt是当前迭代的次数,τ6是包括在0和1之间生成的随机值的向量。在等式中,基于分子除以当前迭代来计算CP的平均力,当前迭代在优化过程中线性增加。因此,CP的平均力的影响逐渐最小化。事实上,这个因素的小值对CPO的性能并不不利,因为它们可能无助于利用迄今为止最好的解决方案周围的各个区域来找到更好的解决方案。因此,通过删除分子并仅依赖于分母,如公式所示。这种方法将有助于在搜索空间内创建广泛的值,从而对迄今为止最好的解决方案周围的区域进行更全面的检查。

CPO-BP 算法
CPO-BP 算法将 CPO 算法与 BPNN 结合,利用 CPO 算法优化 BPNN 的权重和阈值,从而提升模型的预测精度。
CPO-BP 算法流程如下:
利用 CPO 算法初始化 BPNN 的权重和阈值。
使用训练数据对 BPNN 进行训练,并计算误差。
将误差作为 CPO 算法的适应度函数,更新豪猪的位置和刺的大小。
重复步骤 2-3,直至满足停止条件。
BKA(黑翅鸢算法)
原理:
一种模拟黑翅鸢捕食行为的优化算法,它主要用于解决多无人机协同的集群路径规划问题,尤其是在避障路径规划方面。 该算法的核心思想源自于黑翅鸢的群体协作策略,如它们在空中编队飞行和追踪猎物时的灵活性。 在BKA中,每个无人机被看作是一个"粒子",它们的目标是寻找最有效的路径以完成任务,同时避免与其他无人机或障碍物碰撞。
- 初始化:与其他大多数的此类算法一样,采用随机初始化,黑翅鸢的位置作为解。

pop是潜在解的个数,dim是给定问题维数的大小,BKij是第i个黑翅鸢的第j个维数。式中:i为介于1和pop之间的整数,BKlb和BKub分别为第i只黑翅风筝在第j维的下界和上界,rand为[ 0、1 ]之间随机选取的值。
(2)攻击行为
作为小型草原哺乳动物和昆虫的捕食者,黑翅鸢在飞行过程中根据风速调整翅膀和尾角,静静地悬停以观察猎物,然后迅速潜水和攻击。该策略包含针对全局探索和搜索的不同攻击行为。图a展示了一个黑翅鸢在空中盘旋、展翅并保持平衡的场景。
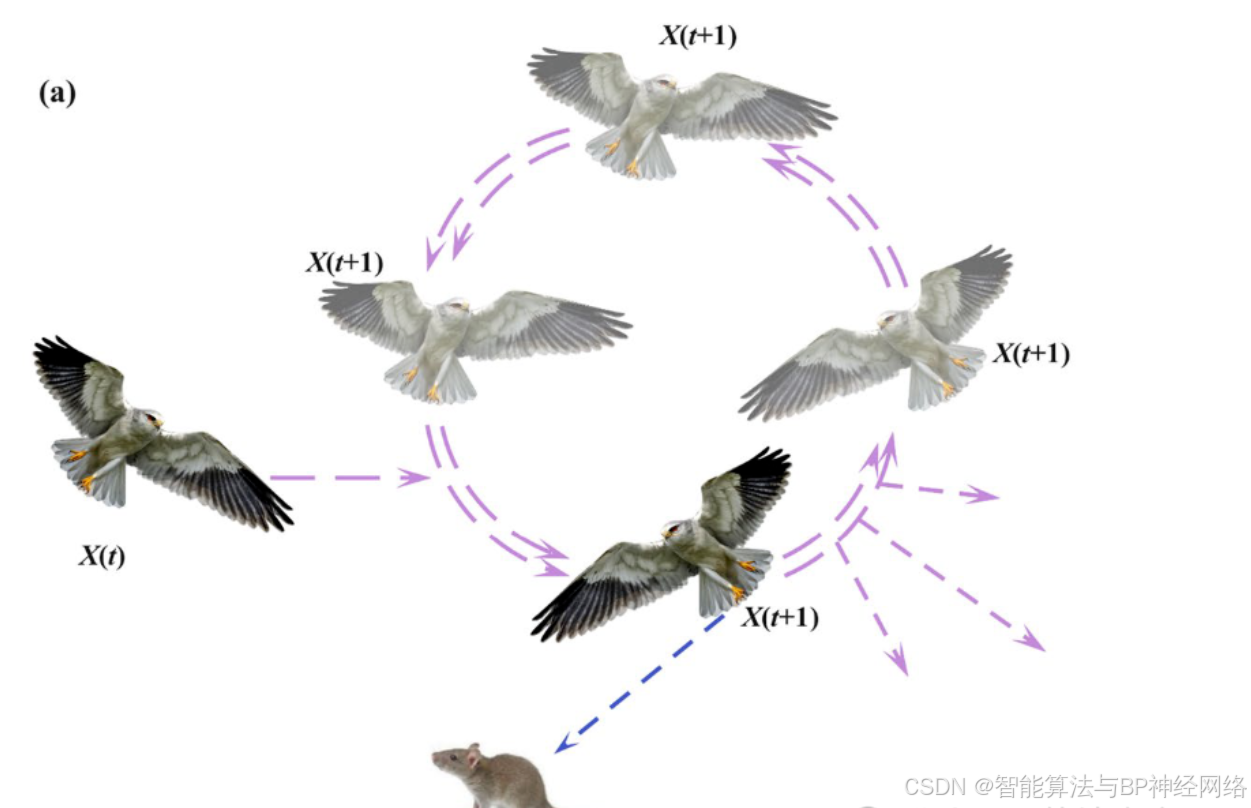

图a展示了一个黑翅鸢在空中盘旋、展翅并保持平衡的场景,且图a展示了黑翅鸢以极快的速度冲向猎物的场景。图b展示了黑翅鸢在空中盘旋时的攻击状态,且图b展示了黑翅鸢在空中盘旋时的状态。下面给出黑翅鸢攻击行为的数学模型:
yi,jt和yi,jt + 1分别表示第i只黑翅鸢在第t步和第(t+1)步迭代中第j维的位置。r是一个取值范围为0到1的随机数,p是一个取值为0.9的常数。T是总的迭代次数,t是到目前为止已经完成的迭代次数。
yi,jt和yi,jt + 1分别表示第i只黑翅鸢在第t步和第(t+1)步迭代中第j维的位置。r是一个取值范围为0到1的随机数,p是一个取值为0.9的常数。T是总的迭代次数,t是到目前为止已经完成的迭代次数。
(3)迁移行为
鸟类迁徙是为了适应季节变化,许多鸟类在冬季从北方向南方迁徙,以获得更好的生存条件和资源。迁移通常由领导带领,他们的导航能力对团队的成功至关重要。
该算法提出了一个基于鸟群迁徙的假设:如果当前种群的适应度值小于随机种群的适应度值,领导者就会放弃领导,加入迁徙种群,说明不适合领导种群向前迁徙。
反之,如果当前种群的适应度值大于随机种群的适应度值,则引导种群直到到达目的地。这种策略可以动态地选择优秀的领导者,保证迁移的成功。上图为黑翅鸢迁徙过程中领鸟的变化情况。下面是关于迁移行为的一个数学模型:
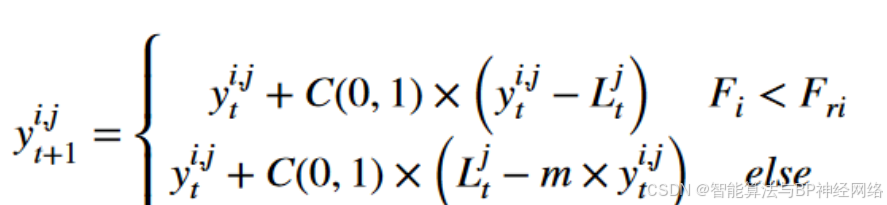

Ljt代表了迄今为止第t次迭代的第j维黑翅鸢的领先得分者(当前最优解)。yi,jt和yi,jt + 1分别表示第i只黑翅鸢在第t步和第(t+1)步迭代中第j维的位置。
C( 0、1 )代表柯西突变( Jiang , et al 2023)。其定义如下:
一维柯西分布是具有两个参数的连续概率分布。下面的方程说明了一维Cauchy分布的概率密度函数:

当δ = 1,μ = 0时,其概率密度函数将变为标准形式。下面是精确的公式:

NRBO(牛顿-拉夫逊优化算法)
原理:
NRBO通过使用几个向量集和两个算子(如NRSR和TAO)来探索搜索域,应用NRM来发现搜索区域,从而定义搜索路径。
一、种群初始化
与其他元启发式算法一样,NRBO通过在候选解的边界内产生初始随机种群来启动对最优解的搜索。基于存在Np个种群的事实,并且每个种群由模糊决策变量/向量组成。因此,使用公式(7)生成随机种群:

其中xij表示第n个总体的第j个维度的位置,rand表示(0,1)之间的随机数。公式(8)给出了可以描绘所有维度的种群的种群矩阵:

二、Newton-Raphson搜索规则(NRSR)
矢量由NRSR控制,允许种群更准确地探索可行区域并获得更好的位置。NRSR是基于NRM的概念,即提出NRM是为了促进勘探趋势并加快收敛。由于许多优化技术是不可微的,因此在这种情况下,使用数学NRM来代替函数的显式公式。NRM从一个假定的初始解开始,并沿着一个确定的方向前进到下一个位置。为了从中公式(5)中获取NRSR,必须使用TS来确定二阶导数。f(x−Δx)和f(x+Δx)的TS如下所示:

通过减去/加上公式(9)和公式(10),得出f'(x)和f'(x)的表达式如下:

代入公式(5)中的公式(11)和公式(12),更新的根位置被重写如下:

考虑到NRSR应该是NRBO的主要组成部分,有必要进行某些调整,以管理种群搜索作为公式(13)的结果。彼此相邻的x的位置分别用xn+Δx和xn−Δx表示,如图2所示。NRBO将这对相邻位置转换为种群中的另外两个向量。因为f(xn)是一个最小化问题,如图2所示。位置xn+Δx的适应度值比位置x差,而位置xn-Δx的适合度比位置xn大。因此,NRBO替换位置Xb的位置xn-Δx,位置Xb在其邻域中具有比位置xn更好的位置,而位置xn+Δx被Xw的位置替换,位置Xw在其邻域内具有比位置xn更差的位置。这个方法的另一个优点是,它使用位置xn而不是其适应度f(xn),这节省了计算时间。因此,NRSR表示如下:

其中randn表示均值为0、方差为1的正态分布随机数,Xw表示最差位置,Xb表示最佳位置。等式(14)可以通过用当前解决方案来辅助更新其位置来增强当前解决方案。等式(14)具有随机参数,以增加NRBO的搜索能力并更好地平衡开发和探索能力。
根据经验,所提出的算法必须能够在多样性和聚集性之间达到平衡,以便在搜索空间中发现最优解,并最终收敛到全局解。可以通过应用一个称为δ的自适应系数来增强算法。δ的表达式如公式(15)所示:

其中IT表示当前迭代,而Max IT表示迭代的最大次数。为了在勘探和开发阶段之间保持平衡,参数δ在迭代过程中会自行调整。图3说明了每次迭代过程中δ的变化。根据公式(15),δ的值在1到−1之间变化。
与自适应参数δ一起,所提出的NRSR通过考虑优化过程中的随机动作、增加多样性和避免局部最优来改进NRBO,同时显著减少迭代次数。公式(14)中Δx的表达式如公式(16)所示:

其中Xb表示迄今为止获得的最佳解,rand(1,dim)是具有dim维度决策变量的随机数。现在,通过考虑NRSR来修改公式(13),并重写如下:

接着,通过包括另一个称为ρ的参数来改进所提出的NRBO的利用,该参数将种群引导到正确的方向。ρ的表达式如下所示。

其中a和b是(0,1)之间的随机数,r1和r2是从总体中随机选择的不同整数。然而,r1和r2的值不相等。矢量的当前位置XnIT已经由公式(19)更新:


其中X1ITn是通过更新xITn而得到的新矢量位置。NRSR是由NRM进一步改进,并且公式(13)被修改和重写如下:

其中yw和yb是使用Z(n+1)和xn生成的两个向量的位置,r1表示(0,1)之间的随机数。NRSR的增强版本如公式(20)所示。使用公式(20)之后,公式(19)被更新如下:


有必要通过用等公式(24)中的当前矢量xnIT的位置代替最佳矢量Xb的位置来构造新矢量X2ITn:

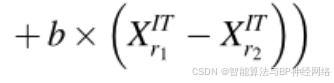
开发阶段是这一搜索方向策略的主要重点。当涉及到局部搜索时,公式(25)提出的搜索方法是有益的,但当涉及到全局搜索时它有局限性;而公式(24)给出的搜索策略对于全局搜索是有益的,但对于局部搜索有局限性。因此,NRBO同时使用公式(24)和(25)来改善多样化和强化阶段。下一次迭代期间的新位置矢量用公式(26)、(27)表示:


其中r2表示(0,1)之间的随机数。
三、陷阱规避操作(TAO)
纳入TAO是为了提高建议的NRBO处理现实世界问题的有效性。TAO是采用Ahmadianfar等人提出的改进和增强运算公式。使用TAO可以显著改变xIT+1n的位置。它通过组合最佳位置Xb和当前矢量位置XITn来产生具有增强质量XITTAO的解决方案。如果rand的值小于DF,则使用如下公式产生解XITTAO:

其中,rand表示(0,1)之间的均匀随机数,θ1和θ2分别是(−1,1)和(−0.5,0.5)之间的一致随机数,DF表示控制NRBO性能的决定因素,μ1和μ2是随机数,分别由公式(31)和(32)生成:

其中β表示二进制数,即1或0,rand表示随机数。如果Δ的值大于或等于0.5,则β的值为0;否则,该值为1。由于参数μ1和μ2选择的随机性,种群变得更加多样化,并逃离局部最优解,这有助于提高其多样性。与NRBO类似,GBO也受到牛顿方法的启发。因此,NRBO概念看起来可能与GBO相似,但由于NRBO的独特特性,其性能仍远优于GBO。
HO(河马算法)
原理;
是一种群智能优化算法, HO算法 是从河马观察到的固有行为中汲取灵感而构思的,例如它们在河流或池塘中的位置更新,对捕食者的防御策略以及逃避捕食者的方法。 该算法通过自适应地调整搜索空间的分辨率和搜索速度,以快速而准确地找到最优解,具有收敛速度快、求解精度高等特点,是一种不错的优化算法。
河马群由几只雌性河马、小河马、多只成年雄性河马和一只占优势的雄性河马(群的首领)组成。
第一种行为由于天生的好奇心,幼河马和小河马经常表现出偏离群体的倾向。因此,它们可能会变得孤立,成为捕食者的目标。
河马的第二种行为模式本质上是防御性的,当它们受到捕食者的攻击或其他生物侵入它们的领地时就会触发。河马表现出防御反应,向捕食者旋转自己,并利用它们可怕的下颚和发声来威慑和击退攻击者。狮子和斑点鬣狗等捕食者意识到了这一现象,并积极避免直接接触河马可怕的下颚,作为预防潜在伤害的措施。
第三种的行为模式包括河马逃离捕食者并积极寻求与潜在危险区域保持距离的本能反应。在这种情况下,河马会努力向最近的水体航行,如河流或池塘,因为狮子和斑点鬣狗经常表现出对进入水生环境的厌恶。
一、种群初始化
HO是一种基于种群的优化算法,其中搜索代理是河马。在HO算法中,河马是优化问题的候选解,这意味着每个河马在搜索空间中的位置更新表示决策变量的值。因此,每只河马都被表示为一个向量,河马种群在数学上由一个矩阵来表征。与传统的优化算法类似,HO的初始化阶段涉及随机初始解的生成。在该步骤中,使用以下公式生成决策变量的向量:

![]()
其中,χi表示第i个候选解的位置,r是0到1范围内的随机数,lb和ub分别表示第j个决策变量的下界和上界。
二、河马在河流或池塘中的位置更新(勘探阶段)
河马群由几只成年雌性河马、小牛河马、多只成年雄性河马和占主导地位的雄性河马(群的首领)组成。基于目标函数值迭代来确定优势河马(最小化问题的最小值和最大化问题的最大值)。通常情况下,河马往往会聚集在彼此很近的地方。占主导地位的雄性河马保护牛群和领地免受潜在威胁。多只雌性河马被安置在雄性河马周围。成年后,雄性河马会被占优势的雄性从牛群中赶走。随后,这些被驱逐的雄性个体被要求吸引雌性,或与牛群中其他已建立的雄性成员进行优势竞争,以建立自己的优势。下式表达了雄性河马的位置:


在等式中(3)中,χi mhippo表示雄性河马的位置,Dhippo表示优势河马的位置(在当前迭代中具有最佳适应度的河马)。r1-r4是0和1之间的随机矢量,r5是0和1之间的随机数(等式4),I1和I2是1和2之间的整数(等式3和6)。
mGi是指一些随机选择的河马的平均值,其包括当前考虑的河马的概率相等(χi),y1是介于0和1之间的随机数(等式3)。在等式中(4)中,q1和q2是整数随机数,可以是1或0。



方程(6)和(7)描述了雌性或未成熟河马在牛群中的位置(χi FB河马)。大多数未成熟的河马都在母亲身边,但由于好奇,有时未成熟的河马会与牛群分离或远离母亲。
如果T大于0.6,这意味着未成熟的河马已经与母亲拉开了距离(等式5)。如果r6是一个介于0和1之间的数字(等式7),大于0.5,这意味着未成熟的河马已经与母亲保持距离,但仍在牛群内或附近,否则,它已经与牛群分离。根据等式(6)和(7)对未成熟和雌性河马的这种行为进行建模。h1和h2是从h方程中的五个场景中随机选择的数字或向量。在等式(7)种,r7是介于0和1之间的随机数。等式(8)、(9)描述了群内雄性和雌性或未成熟河马的位置更新。Fi是目标函数值:


在所提出的算法中,使用h向量,I1和I2场景增强了全局搜索并改进了探索。该算法具有更好的全局搜索能力,提高了探索过程的寻优能力。
三、河马防御捕食者(勘探阶段)
河马群居的主要原因之一可以归因于它们的安全保障。这些庞大而沉重的动物群的存在可以阻止捕食者靠近它们。然而,由于其固有的好奇心,未成熟的河马可能偶尔会偏离牛群,成为尼罗河鳄鱼、狮子和斑点鬣狗的潜在目标,因为与成年河马相比,它们的力量相对较弱。生病的河马和未成熟的河马一样,也容易被捕食者捕食。
河马采用的主要防御策略是迅速转向捕食者并发出响亮的叫声,以阻止捕食者靠近它们(图2)。在这一阶段,河马可能会表现出接近捕食者以诱导其撤退的行为,从而有效地抵御潜在的威胁。方程(10)表示捕食者在搜索空间中的位置:
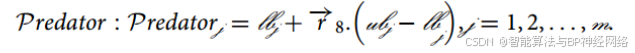
其中表示一个从0到1的随机向量。

等式(11)表示第i只河马到捕食者的距离。在这段时间里,河马采取了基于FPredatorj因素的防御行为,以保护自己免受捕食者的攻击。如果FPredatorj小于Fi,表明捕食者离河马非常近,在这种情况下,河马会迅速转向捕食者,并向其移动,使其后退。如果FPredatorj更大,则公式(12)表明捕食者或入侵河马的领地更远。在这种情况下,河马转向捕食者,但活动范围更为有限。其目的是让捕食者或入侵者意识到其在其领土内的存在。
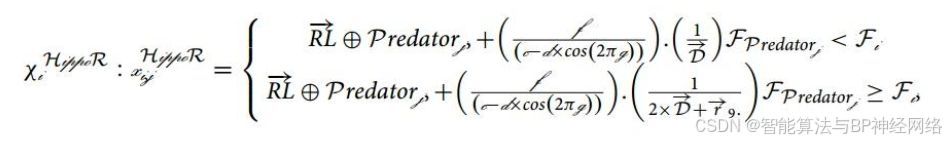

χi HippoR是河马面对捕食者时的姿势→RL是一个具有Levy分布的随机向量,用于攻击河马时捕食者位置的突然变化。Lévy运动46的随机运动的数学模型计算为等式(13)。w和v是0-1之间随机数,Ŵ是伽玛函数的缩写,σw可以通过计算等式(14)获得。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








