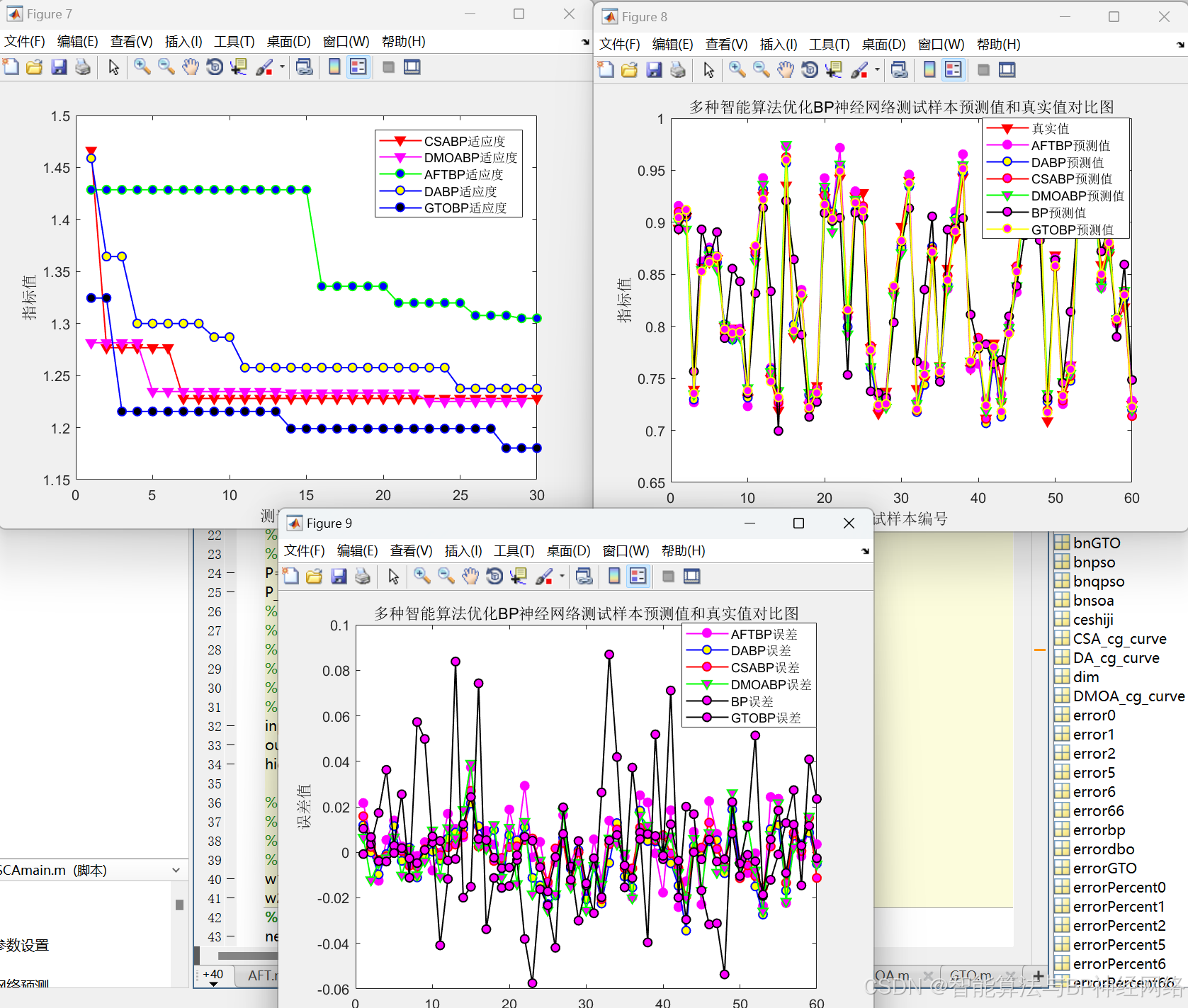
多种智能算法优化BP神经网络实现数据回归预测（蜻蜓算法优化BP(DABP),矮猫鼠鼬算法优化BP(DMOABP)人工大猩猩算法优化BP(GTOBP)阿里巴巴与四十大盗算法优化BP(AFTBP)）

代码运行效果截图：

代码运行采用的数据集：

1. 五种智能算法优化BP神经网络详细讲解

2.一种全新的论文大法：改进型智能算法优化BP+多目标优化算法（创新性+工作量）

3.如何使用BP神经网络预测数据

CPO_BP：（2024最新算法）冠豪猪算法优化BP神经网络

DMOA_BP：（2023）矮猫鼬算法优化BP神经网络

CSA_BP：（2021年新型元启发式优化方法（合作优化）

AFT_BP:(阿里巴巴与四十大盗算法优化BP神经网络)

DA_BP:(蜻蜓算法2019)

GTO_BP:(人工大猩猩部队算法优化BP神经网络

CPO_BP：（2024最新算法）冠豪猪算法优化BP神经网络

原理：

1.冠豪猪优化算法 (CPO)

CPO 算法是一种基于生物启发的优化算法，其灵感来源于豪猪的防御机制。豪猪在遇到威胁时会竖起刺毛，并释放出气味，从而吓退敌人。CPO 算法将豪猪的刺毛模拟为搜索空间中的解，并将刺毛的长度和方向与解的优劣程度联系起来。算法通过不断调整解的刺毛长度和方向，逐步找到最优解。

CPO 算法的主要步骤如下：

初始化豪猪群体，并随机生成每个豪猪的刺毛长度和方向。

评估每个豪猪的适应度，即解的优劣程度。更新豪猪的刺毛长度和方向，使其朝着更优的解方向移动。重复步骤 2-3，直到满足停止条件。

2.冠豪猪算法优化bp神经网络（CPO-BP 算法）

CPO-BP 算法将 CPO 算法与 BPNN 结合，利用 CPO 算法优化 BPNN 的权重和阈值，从而提升模型的预测精度。

CPO-BP 算法流程如下：

利用 CPO 算法初始化 BPNN 的权重和阈值。

使用训练数据对 BPNN 进行训练，并计算误差。

将误差作为 CPO 算法的适应度函数，更新豪猪的位置和刺的大小。重复步骤 2-3，直至满足停止条件。

DMOA_BP：矮猫鼬算法优化BP神经网络

原理：

1.矮猫鼬优化算法（DMOA）

矮猫鼬优化算法（DMOA）是一种新型的群体智能优化算法，该算法模拟了非洲矮猫鼬觅食和躲避天敌的行为，具有以下特点：

具有较强的全局搜索能力；
对参数调整不敏感；
可以有效地避免陷入局部最优解。

CSA_BP：（合作优化算法bp神经网络

原理：

合作优化算法（CSA）

是一种新型元启发式优化算法，该算法受现代企业团队协作行为的启发，具有搜索速度快、寻优能力强的特点。CSA算法通过团队组建，团队沟通，反思学习，内部竞争四个主要操作模拟了现代企业团队协作行为，最后选取最优解。

1）团队组建阶段

在这一阶段，随机确定团队中的所有员工，在评估所有解决方案的绩效后，从初始群体中选择M∈[1,I]领导解决方案，形成外部精英集。公式如下

其中是当前群体的解决方案的数量。是第i个解在第k周期的第j值。φ(L, U)是生成均匀分布在[L, U]范围内的随机数的函数。

（2）团队沟通阶段

每个员工都可以通过与董事长、董事会、监事领导的信息交流获得新的信息。数学模型如下式表示：

其中是第k+1个循环时第i群解的第j值。团队沟通过程包括董事长知识A、董事会集体知识B和监事会集体知识C三个部分。董事长从董事会中随机抽取，模拟轮换机制，董事会和监事的成员在计算B和C时被赋予相同的职位。数学模型如下式表示：

其中是第k个周期中第i个个人最y优解的第j个值。是从第一个循环开始到第k个循环的第n个全局知名解的第j个值。ind是集合{1,2，…， m}。表示从外部精英集合中随机选择的董事长获得的知识。和分别是从迄今为止发现的M个全球最优解和个个人最优解中获得的平均知识。α和β为调整和影响程度的学习系数。

（3)反思学习阶段

除了向领导学习解决方案外，员工还可以从相反的方向总结自己的经验来获得新的知识，数学模型表达式为: 其中为第i个反射解在第k+1个循环时的第值。

（4)内部竞争阶段

团队逐步提升市场竞争力，确保所有业绩较好的员工都能被保留下来，数学模型表达式为:

其中，F (x)为解x的适应度值。

AFT_BP:(阿里巴巴与四十大盗算法优化bp神经网络)

原理：

1.阿里巴巴与四十大盗算法优化bp神经网络

AFT将阿里巴巴比作目标函数的最优解，而四十大盗则是代表搜索空间中的解，它们通过一系列操作和协作来寻找最优解。

算法过程

案例一：得到信息，追寻阿里巴巴

案例二：被欺骗，随机探索

案例三：平衡全局与局部

DA_BP:(蜻蜓算法优化bp神经网络)

原理：

蜻蜓算法（DA）

蜻蜓集群有两种行为目的：狩猎（静态集群）和迁徙（动态集群）。静态集群中，蜻蜓分成小群捕猎，局部移动和突然飞行路径变化是其特征。动态集群则是大量蜻蜓在单一方向上长距离迁徙。这两种行为类似于元启发式优化中的探索和开发利用阶段，静态集群探索不同区域，而动态集群利用大群体沿着一个方向飞行。

群体的行为遵循三个基本原则：

分离（Separation）：指个体在邻域内静态地避免与其他个体碰撞
对齐（Alignment）：表示个体的速度与邻域内其他个体的速度匹配
凝聚（Cohesion）：指个体朝向邻域质心的趋势
分离：

其中，Xj表示第i只蜻蜓领域内其他蜻蜓，Si表示第i只蜻蜓分离位置向量。

对齐：

其中，Ai表示第i只蜻蜓与领域内其他蜻蜓对齐的位置向量。

凝聚：

其中，Ci表示第i只蜻蜓凝聚时的位置向量。

寻找食物：

其中，X+表示猎物位置。

躲避天敌：

其中，X-表示天敌位置。

位置更新：

式中参数均为权重因子。

为了提高DA随机性和探索能力，当没有邻近解时，它们需要在搜索空间中进行Lévy飞行：

Lévy函数表述如下（Mantegna算法）：

GTO_BP:(人工大猩猩部队算法优化bp神经网络)

原理：

1.人工大猩猩部队算法（GTO）

模拟大猩猩全体的生活行为来进行寻优，具有寻优能力强，收敛速度快等特点。

GTO通常遵循以下几个规则来搜索解决方案：

1.1GTO算法的优化空间包含三种类型的解决方案，其中X被称为大猩猩的位置向量，GX被称为大猩猩候选位置向量，在每个阶段创建，如果其性能优于当前解决方案，则更新。最后，银背猩猩silverback是每次迭代中找到的最佳解决方案。

1.2考虑到为优化操作选择的搜索种群的数量，整个群体中只有一只银背猩猩。

1.3三种类型的X、GX和silverback解决方案精确模拟了大猩猩在自然界中的社交生活。

1.4大猩猩可以通过寻找更好的食物来源或在一个公平而强壮的群体中定位来增加它们的力量。在GTO中，在GTO算法中称为GX的每次迭代中都会创建解决方案。如果找到的解决方案是新的（GX），它将替换当前的解决方案（X）。否则，它将保留在内存中（GX）。

1.5大猩猩倾向于集体生活，因此无法单独生活。因此，他们作为一个群体寻找食物，并继续生活在一个银背猩猩的领导下，领导着所有的群体决策。在我们的公式化阶段，假设种群中最差的解是大猩猩群中最弱的成员，大猩猩试图避开最差的解，接近最佳解（银背），从而改善大猩猩的所有位置。

1.1.1勘探阶段

其中， p pp 是一个给定的介于 0 到 1 之间的参数，该参数确定选择迁移机制到末知位置的概率：GX(t+1) 是下次迭代时大猩猩个体的候选位置向量：X(t) 是大猩猩个体的当前位置向；r1,r2,r3和rand 是在每次迭代中更新的范围为 0 到 1 的随机值；UB 和LB 分别表示变量的上限和下限； Xr和GXr分别是从整个种群中随机选择的大猩猩中的一员，随机选择的大猩猩候选位置向量，包括每个阶段更新的位置； C,L 和 H 的计算如下：

其中， It 是当前迭代次数， MaxIt为最大迭代次数，cos表示余弦函数，r4 是0到1的随机值； l为-1到1之间随机值。Z是问题维度中范围为 [−C,C] 的随机值。在探索阶段结束时，计算所有 GX 个体的适应度值，如果适应度值满足GX(t)<X(t) ，则使用GX(t) 个体作为 X(t) 新个体。并且该阶段产生的最优个体被视为银背大猩猩即最优解。

1.2 开发阶段

在GTO算法的开发阶段，采用了跟随银背大猩猩和竞争成年雌性的两种行为。银背大猩猩领导一个群体，做出所有决定，决定群体的行动，并引导大猩猩走向食物来源。它还负责团队的安全和福祉，团队中的所有大猩猩都遵守银背大猩猩的所有决策。另一方面，银背大猩猩可能会变弱、变老并最终死亡，群体中的黑背大猩猩可能会成为群体的领导者，或者其他雄性大猩猩可能会与银背大猩猩交战并主宰群体。开发阶段使用的两种机制所述，可以使用式(2)中的数值选择跟随银背或竞争成年此惟。如果 C≥W ，则选择跟随银背机制，但如果 C<W ，则选择竞争成年雌性机制。W 是优化操作之前要设置的参数。

1.2.1 跟随银背大猩猩

如果C≥W ，则选择跟随银背大猩猩机制，其行为如式(7)所示：

其中，X(t) 是大猩猩的位置向量，X silverback是银背大猩猩的位置向量(最佳位置)，此外， L 由式(4)计算， M 由式(8)计算；GXi(t) 表示每个候选大猩猩在第 t次迭代时的位置向量， N表示大猩猩个体的总数(种群规模)， g由式(9)计算所得；在式(9) 中， L由式(4)计算所得。

1.2.2 竞争成年雌性

如果C<W ，则选择开发阶段的第二个机制。一段时间后，当年轻的大猩猩进入青春期时，它们会与其他雄性大猩猩在选择成年䧳性的问题上展开竞争，这种竞争通常是激烈的。式(10)模拟了这种行为。

其中，Xsilverback 为银背大猩猩的位置向量(最佳位置)， X(t) 为当前大猩猩个体的位置向量， Q用于模拟冲击力， r5是0到1间的随机值，A为冲突中暴力程度的系数向量 ; β是在优化操作之前给定的参数值， E使用式(13)进行评估，同时用于模拟暴力对解决方案维度的影响。如果 rand≥0.5 ，则 E的值将等于正态分布和问题维度中的随机值；但如果rand<0.5 ，E将等于正态分布中的随机值。rand是介于 0 和1之间的随机值。在开发阶段结束时，进行一次群体操作，在该操作中，估计所有GX 个体的适应度值，如果适应度值满足GX(t)<X(t) ，则使用GX(t) 作为 X(t) 个体，并将在整个种群中获得的最佳解视为银背大猩猩。

智能算法改进方式：

1.初始化种群：

a.混沌映射（23种cubic,cricle,tent）（数学非线性微分方程没解析解图形描述解）

b.反对立学习/复合策略反对立学习（cobl）

c.Levy飞行

d.最优拉丁超立方/拉丁超立方（LSH）（统计上）

e.Sobel序列（滤波）

f.方形领域拓扑结构

g.无线折叠混沌

2.个体迭代更新变异

a.量子行为（QPSO）

b.双样本学习