【最长上升子序列】洛谷P3902_递增

最新推荐文章于 2024-07-21 21:41:35 发布

num21212

最新推荐文章于 2024-07-21 21:41:35 发布

阅读量452

点赞数

CC 4.0 BY-SA版权

分类专栏：模板

本文链接：https://blog.youkuaiyun.com/qq_42937087/article/details/99605231

模板专栏收录该内容

10 篇文章

订阅专栏

本文介绍了如何解决洛谷P3902问题，即求解最长上升子序列。攻略包括两种策略：当新数大于序列末尾数时直接追加；否则，在序列中找到合适位置插入新数。最后，答案为序列的最长长度，而非原序列长度与最长序列长度之差。

逐·渐·中·二

拒绝大魔王，来一道简单点的题怪水一水。

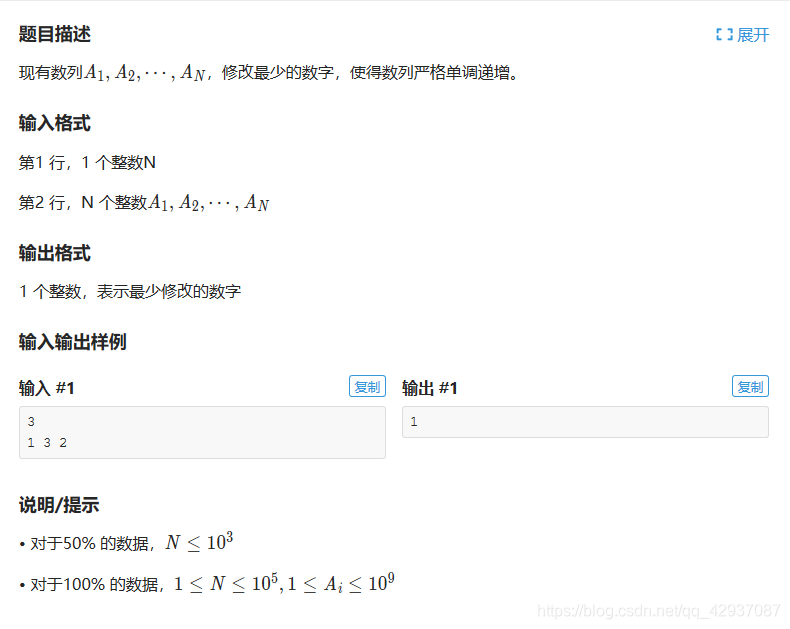
怪物种类：最长上升子序列
等级：橙题(shui(bu
打怪攻略：
1.用一个序列s存最长上升子序列，然后对于一个新的数a，如果它大于序列末尾的数，那么序列s末尾就接上a。
2.不然就在序列s中找一个sl<a<=sr的位置，将a存到r位置上。
答案就是序列最长的长度。
此怪非模板，需要输出用n减去序列最长长度。

#include<cstdio>
#include<iostream>
using namespace std;
int n,a,t,ans[100003],maxx;
 int main(){
 	scanf("%d",&n);
 	for(int i=1;i<=n;++i){
 		scanf("%d",&a);  //读入
 		if(a>ans[t]){  //如上1
 			++t;
 			ans[t]=a;
 			maxx=max(maxx,t);
 		}
 		else{  //如上2，二分查找那个位置。
 			int l=1,r=t;
 			while(l<r){
 				int mid=(l+r)>>1;
 				if(ans[mid]<a) l=mid+1;
 				else r=mid;
 			}
 			ans[l]=a;  //存
 		}
 	}
 	printf("%d",n-maxx);   //输出
 }