Audiophobia UVA - 10048 噪音恐惧症最短路

最新推荐文章于 2022-08-30 17:53:33 发布

Nicolas Lee

最新推荐文章于 2022-08-30 17:53:33 发布

阅读量885

点赞数 1

CC 4.0 BY-SA版权

分类专栏：图论文章标签：最短路 c++ uva Floyd算法

本文链接：https://blog.youkuaiyun.com/qq_42835910/article/details/88092707

图论专栏收录该内容

19 篇文章

订阅专栏

本文介绍了一种基于Floyd算法的改进方法，用于寻找两点间噪声值最小的路径。通过将加法替换为min函数，min替换为max，解决了在噪声图中寻找最优路径的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接

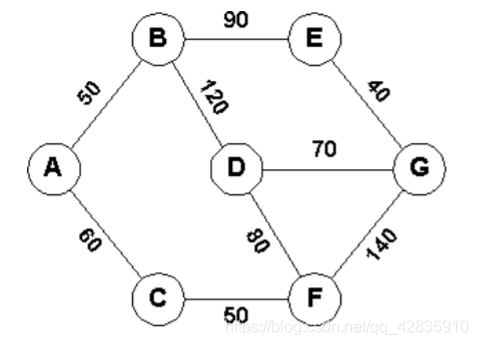
输入一个C个点S条边（C≤100，S≤1000）的无向带权图，边权表示该路径上的噪声值。当噪声值太大时，耳膜可能会受到伤害，所以当你从某点去往另一个点时，总是希望路上经过的最大噪声值最小。输入一些询问，每次询问两个点，输出这两点间最大噪声值最小的路图。例如，在图中，A到G的最大噪声值为80，是所有其他路径中最小的（如ABEG的最大噪声值为90）。

【分析】
本题的做法十分简单：直接用floyd算法，但是要把加法改成min，min改成max。为什么可以这样做呢？不管是floyd算法还是dijkstra算法，都是基于这样一个事实：对于任意一条至少包含两条边的路径i->j，一定存在一个中间点k，使得i->j的总长度等于i->k与k->j的长度之和。对于不同的点k，i->k和k->j的长度之和可能不同，最后还需要取一个最小值才是i->j的最短路径。
把刚才的推理中“之和”与“取最小值”换成“取最小值”和“取最大值”，推理仍然适用。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100+5, INF = 0x3f3f3f3f;
int g[N][N];
int main(int argc, char** argv) {
	int c, s, q, kase = 0;
	while(scanf("%d%d%d",&c,&s,&q) == 3 && c){
		memset(g, INF, sizeof(g));
		for(int i = 0; i < s; i++){
			int u, v, d;
			scanf("%d%d%d",&u,&v,&d);
			g[u][v] = g[v][u] = d;
		}
		for(int k = 1; k <= c; k++)
			for(int i = 1; i <= c; i++)
				for(int j = 1; j <= c; j++)
					g[i][j] = min(g[i][j], max(g[i][k], g[k][j])); 
		if( kase) printf("\n");
		printf("Case #%d\n", ++kase);
		while(q--){
			int u, v;
			scanf("%d%d",&u,&v);
			if(g[u][v] == INF) printf("no path\n");
			else printf("%d\n",g[u][v]);
		}
	}
	return 0;
}