图论：Prim算法与Kruskal算法实现最小生成树（C++）

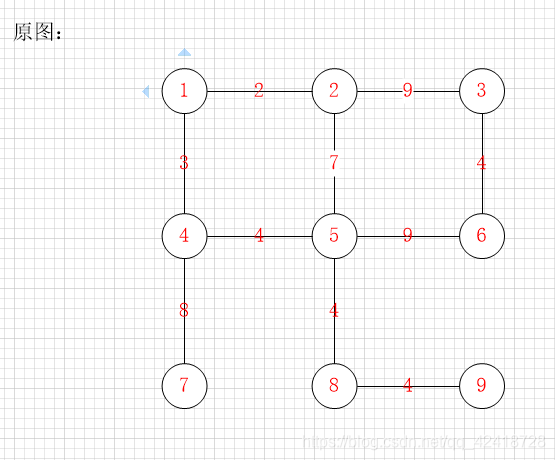
要求最小生成树的图： 

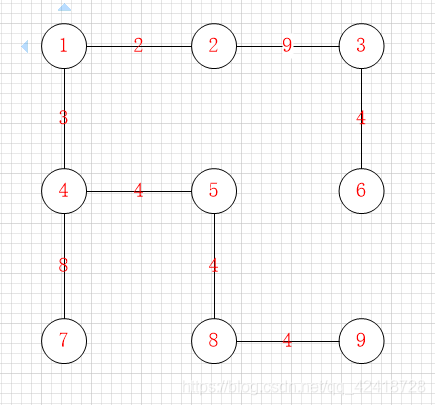
目标生成树： 生成树最小权值：38

---

1.Prim算法：

从一个点到其他点的距离数组中取最小的点，并用新取点到其他点的距离更新初始距离数组，再次对此取点…

邻接权值矩阵：
0 2 0 3 0 0 0 0 0
2 0 9 0 7 0 0 0 0
0 9 0 0 0 4 0 0 0
3 0 0 0 4 0 8 0 0
0 7 0 4 0 9 0 4 0
0 0 4 0 9 0 0 0 0
0 0 0 8 0 0 0 0 0
0 0 0 0 4 0 0 0 4
0 0 0 0 0 0 0 4 0

实现代码：

#include<iostream>
#define INFINF 9999
using namespace std;
/*
 *BFS 最小生成树Prim算法：
 */
int len[10][10];
int SumWeight=0;

int main()
{
	int currentLen[10];
	cout << "putin 9X9 arraylist: "<< endl;
	for(int i=1;i < 10;i++){
		for(int j=1;j < 10;j++){
			cin >> len[i][j];
			if(0 == len[i][j])
			len[i][j] = INFINF;
			if(i == j)
			len[i][j] = -1;
		}
	}
	//初始化广搜距离数组 
	for(int i=1;i < 10;i++)
	currentLen[i] = len[1][i];
	currentLen[0] = INFINF;
	//找出n-1条边 
	for(int i=1;i < 9;i++){
		int min=0;
		//找出当前距离数组中最小的未选权值边 
		for(int j=1;j < 10;j++)
			if(currentLen[min] > currentLen[j]&&currentLen[j]!=-1)
			min = j;
		SumWeight += currentLen[min];
		currentLen[min] = -1;
		//更新广搜距离数组 
		for(int k=1;k < 10;k++){
			if(len[min][k] < currentLen[k]&&currentLen[k]!=-1)
			currentLen[k] = len[min][k];
		}
	}
	cout << "Minument SumWeight is :" << SumWeight << endl; 
	return 0;
}

---

2.Kruskal算法：

从所有的边集合中找出尽量小的且不构成回路的边加入生成树的边集合。

输入第一行：边数、点数

接下来n行为  边两个顶点以及权值

实现代码：

#include <iostream>
#include <algorithm>
#define INFINF 9999
#define Maxsize 1000
using namespace std;
struct node{
	int lp;//left point 
	int rp;//right point
	int cost;//代价 
}; 
struct node edgeA[Maxsize];//原图的边集 
struct node edgeB[Maxsize];//生成树的边集 
int n,m;//n为边数，m为点数 
int sumcost=0;
//初始化并查集 
int S[Maxsize];
int Slen;
void initS(int num){
	for(int i=1;i <= num;i++){
		S[i]=i;
	}
	Slen = num;
}
//集合的合并 
void join(int l,int r){
	int x,y;
	if(S[l] < S[r]){
		x = S[l];
		y = S[r];
	}else if(S[l] > S[r]){
		x = S[r];
		y = S[l];
	}
	else return;
	for(int i=1;i <= Slen;i++){
		if(S[i] == y)
		S[i] = x;
	}
}
void Kruskal(struct node edgeA[], struct node edgeB[]){
	int cur=1;
	edgeB[cur]=edgeA[1];
	sumcost+=edgeA[1].cost;
	join(edgeA[1].lp,edgeA[1].rp);
	for(int i=2;i <= n;i++){
		if(S[edgeA[i].lp] != S[edgeA[i].rp]){
			edgeB[++cur] = edgeA[i];
			sumcost+=edgeA[i].cost;
			join(edgeA[i].lp,edgeA[i].rp);
		}
	}
}
bool cmp(struct node a,struct node b){
	return a.cost < b.cost;
}
int main(){
	cout << "put in number of Graph Edges:" << endl;
	cin >> n;
	cout << "put in number of Graph Point:" << endl;
	cin >> m;
	cout << "put in the points & cost of every struct nodes:" << endl;
	for(int i=1;i <= n;i++)
	cin >> edgeA[i].lp >> edgeA[i].rp >> edgeA[i].cost;
	std::sort(edgeA+1,edgeA+n+1,cmp);
	initS(m);
	Kruskal(edgeA,edgeB);
	cout << "the least cost of Graph Creat Tree: " << sumcost << endl;
	return 0;
}