PI参数的离散化的文章可以看:PID控制器的数字实现及C语法讲解 - free_稀饭 - 博客园 (cnblogs.com)
三个参数的作用:
-
Kp参数:能迅速反映误差,从而减小误差,但他不能消除稳态误差,加大Kp还会引起系统的不稳定。
-
Ki参数:只要有足够的时间,积分作用将能完全消除误差。但其缺点积分控制是偏差累积控制,控制作业缓慢,但是如果积分作用太强会使系统的超调量加大,甚至出现振荡。
-
Kd参数:预测误差变化趋势,减小超调量,克服振荡,使系统的稳定性提高,还能加快系统的动态响应速度,减小调整时间,从而改善系统的动态性能。
1 连续型PID算法
1、理想形式:
2、并行形式: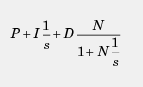
也可写为:








 本文详细介绍了PID算法的连续型和离散型,包括位置式和增量式两种形式,重点阐述了每种形式的特点和适用场景。此外,还探讨了谐振控制器的概念,提供了不同离散方法的实现,如Trapezoid方法,并给出了C语言实现的例子。
本文详细介绍了PID算法的连续型和离散型,包括位置式和增量式两种形式,重点阐述了每种形式的特点和适用场景。此外,还探讨了谐振控制器的概念,提供了不同离散方法的实现,如Trapezoid方法,并给出了C语言实现的例子。

 订阅专栏 解锁全文
订阅专栏 解锁全文

















 648
648

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








