经典递归：汉诺塔问题

经典递归：汉诺塔问题

游戏规则1.一次一片（没用）
游戏规则2.大不压小（关键）等价于：大上有小，大不能动

性质1：任意时刻一根柱子上如果有多个片子摞在一起，它们都是自下而上，从大到小的 — ‘▲’ 形（小的上面只能放再小的，上面放更小的，以此类推，不可能出现大的（像极了我们的社会，泪目））
性质2：除了目标柱子，其他柱子都等价（我心里只有你，其他人都是浮云，什么杀马特…），这条性质，emmm 就假装柱子可以掰下来换位置吧，但目标柱不一样，他有历史意义（我瞎说的不知道对不对）

• 以3根柱（A出生柱，B非目标柱，C终点柱）为例:

一、屁股坐下去才是一切的开始！

把一坨从这里挪到那里的，最关键一步是屁股挪（最下面那个）过去，因为屁股具有两个性质：
屁股性质1：这坨里的所有片中，屁股一定是最先挪过去的（其他都比屁股小，若先挪过去，屁股就坐不下了）
屁股性质2： 屁股一旦就位（坐实了），他就不用再挪地儿了，完全与底盘融为一体（因为屁股是这坨里最大的，其他的盘子在屁股上横行没有任何顾虑），所以把屁股挪到目标柱以后，接下来就可以无视屁股（减小问题规模），片数 - -

二、屁股怎么做？

所以来看挪屁股这一关键步骤：

1. 首先，挪屁股的前提是：
   a.) 屁股上没东西压它（规则2：大上有小不能动）
   b.) 目标柱上没得其他片。这不必说，屁股最大，其他都是弟弟，有弟弟在屁股挪不过去（规则2：大不压小）
   =》所以说这一操作：屁股一个人完完全全占了两个位置
2. 由此可知，其他弟弟在哪里？----- 只能萎缩在最后一根柱子上，由性质2可知，这其他n-1个盘子，只能 ▲ 形排列在那跟柱子上，发现了吗？这n-1个弟弟不就是少了一个屁股的另一小坨（好，我们给这小坨起个名字，不如就叫 “没屁股的弟弟”）
3. 到这里很关键了，可惜没有图，脑补一下吧。总结来说，我们挪n个盘子的次数O(n)由3部分组成：①挪屁股这一关键步骤前的步骤，②挪屁股（1步），③挪屁股之后的一系列步骤
4. 别忘了，屁股粘地，毁天灭地（见 屁股性质2），这一性质有两个用处：
   a.) 挪完屁股，就可以消去屁股
   b.) 挪屁股以前，更准确的说是，紧贴着屁股那个弟弟从他身上剥离之前，屁股也是一直沾地，也完全可以无视（★）
5. 由 3 .4 可知：①→②→③ 的过程去掉粘地的屁股，就完全可以看成是：
   ① “没屁股的弟弟”从出生柱挪到另一个非目标柱（这两个柱子等价！） →
   ② 挪屁股：把刚才粘在出生地上装死的屁股撕下来，贴到终点地上继续装死 →
   ③ “没屁股的弟弟”从那个非目标柱移到终点柱（屁股上）
   因为性质2 非目标柱完全可以看成新的出生柱，所以① 和③，从抽象意义上来看，都是“没屁股的弟弟”从出生柱挪到终点柱。这似曾相识的过程，怕不就是最开始问题的弟弟版（-= 屁股），我们设这个弟弟版需要的次数为O(n-1)
6. 由3.中等式： O(n) = O(n-1) + 1 + O(n-1), 即O(n) = 2*O(n-1) + 1; 其中：O(1) = 1

---

POJ

样例输入

3 a b c

样例输出

1:a->c
2:a->b
1:c->b
3:a->c
1:b->a
2:b->c
1:a->c

• 思路1：
  见前面一堆比比

• code1:

#include <iostream>
using namespace std;

void Hanoi(int n, char born, char mid, char end){
	if(n == 1)
		printf("1:%c->%c\n", born, end);
	else{
//		printf("%d:%c->%c\n", n, born, end);
		Hanoi(n-1, born, end, mid);
		printf("%d:%c->%c\n", n, born, end);
		Hanoi(n-1, mid, born, end);
	}
}

int main(){
	int n; 
	char a, b, c;
	scanf("%d %c %c %c", &n, &a, &b, &c);
	Hanoi(n, a, b, c);
	
	return 0;
}

• 相关文章
  作者：YIHE陳
  链接：https://www.zhihu.com/question/24385418/answer/46241635
  来源：知乎
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

懒汉式递归——瞬间明白汉诺塔问题Q. 为什么会有递归？A. 因为我们是人，不是电脑！我们的workingmemory有限！游戏规则：有A,B,C三根针，将A针上N个从小到大叠放的盘子移动到C针，一次只能移动一个，不重复移动，小盘子必须在大盘子上面。问题：总的移动次数是多少？分析：首先明确，我们的目标是将A针上所有N个盘子移动至C针。而对于B针，我们可以将之看成一个中转站。这个问题，顺向思维或者逆向思维道理是相同的，都太麻烦。我们不妨从中间开始思考。||： 规则要求小盘子必须在大盘子之上。试想这个过程中，必然会经历那么一个步骤，即有一大坨N-1个盘子在B针这个中转站，而我们正将最大那个盘子（即第N个盘子）从A针移动至C针。

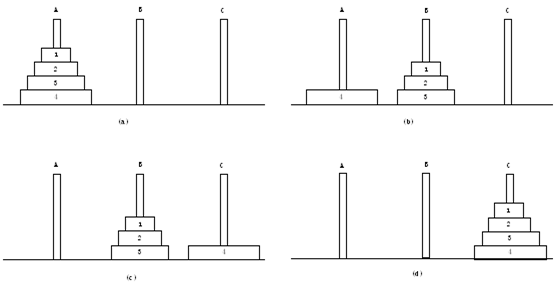
【图例】只有经历“移动最大盘子”这个步骤，余下的事情才有可能实现。而在此之前，我们所要做的事情，就是让“移动最大盘子”这个步骤得以实现。现在，游戏整个过程以“移动最大盘子”为中央，被分为了两部分。即（前）“将那坨N-1个盘子从A针移动到B针”，(中)“移动最大盘子”，(后)“将坨N-1个盘子从B针移动到C针”。这是我们意识到，（前）与（后）操作道理是相似的。不去管那个最大盘子，（前）是以C针为中转站，（后）是以A针为中转站。因此两者所需的移动次数应当是相等的。这意味着我们只要计算出其中一者的移动次数，然而乘以2，在加上“移动最大盘子”的那1次，就是这场游戏的总移动次数了。用数学语言表达，假设（前）“将N-1个盘子从A针移动到B针”所需次数为Hn-1，总移动次数为Hn，那么可以得出的关系就是：Hn=Hn-1x 2 + 1.其实当我们得出这个算式的时候，稍微聪明一点的人已经明白，这就是一个递推公式，可以直接用此公式得出Hn的通解。但是LZ比较笨，就是不明白，为什么这个公式就可以套用呢？那么就干脆继续思考吧。让我们再想象一个情景：最大那个盘子在刚刚从A针被移动到C针，而那坨N-1个盘子还在B针蠢蠢欲动地等待着，即处于（中）->(后)的这个状态。怎么移动这N-1个盘子呢？其实这时候，问题已经回到了笔者标示“||：”符号的地方。“||：”是乐谱中的反复记号，而我们要做的，就是重复上面的步骤，但是要将N替换为N-1，因为现在只剩下N-1个盘子需要移动。而中转站则从B变成了A（鉴于这时盘子都在B针）。目标仍然是C针。下一次重复的时候，只剩下N-2个盘子需要移动，中转站又回到B，目标不变仍然是C针。……整个过程中，变化的只是中转站（在A与B之间轮换），以及剩下那些所需要移动的盘子的总数（越来越少）而已。那么那个大盘子怎么办？不去管它吗？？正解！！因为你已经把它移到C针，已经完成了这个移动步骤，它不会影响之后的操作。提醒自己牢记游戏规则，大盘子永远在小盘子下面，而你也不需要再重复移动它——“不重复移动”，正是游戏规则的要求！于是Hn=Hn-1 x 2 + 1 这个公式，就可以套用、套用、套用……直到H3=7，H2=3，H1=1。最后，用最懒的数学归纳法证明通项公式Hn = 2^n - 1 吧！没办法，LZ就是比较懒嘛~Fin.