向量链式法则:
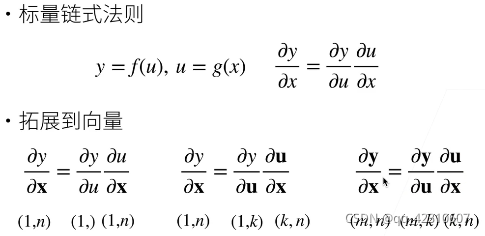


自动求导:(计算一个函数在指定值上的导数)
计算图:
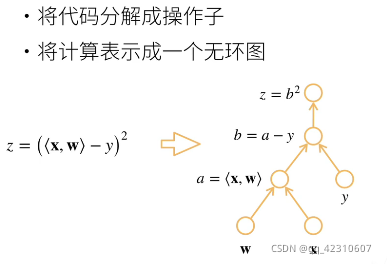

自动求导的两种模式:(正向和反向)
 这篇博客深入探讨了自动求导的概念,包括向量链式法则,以及其在计算函数导数中的应用。通过介绍计算图,解释了自动求导的正向和反向模式,并讨论了它们的复杂度。此外,文中提出了一些课后练习,如比较一阶和二阶导数的计算开销,以及在不同输入情况下反向传播的影响,强调了在控制流中分析梯度的重要性。最后,通过一个具体的例子展示了如何绘制sin(x)及其导数的图像,不依赖于标准导数公式。
这篇博客深入探讨了自动求导的概念,包括向量链式法则,以及其在计算函数导数中的应用。通过介绍计算图,解释了自动求导的正向和反向模式,并讨论了它们的复杂度。此外,文中提出了一些课后练习,如比较一阶和二阶导数的计算开销,以及在不同输入情况下反向传播的影响,强调了在控制流中分析梯度的重要性。最后,通过一个具体的例子展示了如何绘制sin(x)及其导数的图像,不依赖于标准导数公式。
向量链式法则:
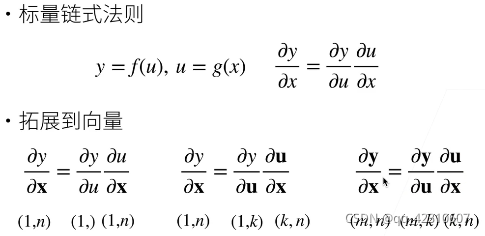


自动求导:(计算一个函数在指定值上的导数)
计算图:


自动求导的两种模式:(正向和反向)
 1803
1803
 8520
8520

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


