算法设计 algorithm design 第八章NP问题以及计算难解性 NP and Computational Intractability

---

1 Definition 定义

1.1 decision problem 判定问题：

• 该问题称为X
• instance string s 一个实例s
• algorithm A solves problem X: $A(s)=yes$ iff $s\in X$

判定问题是指我们常说的判断题，返回yes或者no。注意定义中的$s\in X$ 等价于$A(s)=yes$。
我们后续研究的问题都是判定问题。所有的优化问题可与规约到判定问题。

1.2 polynomial time 多项式时间：

• 对于所有的实例s, A(s)至多在多项式步骤内终止。

1.3 P 问题：

• 有多项式时间算法的判定问题

1.4 NP问题

问题，实例，可能的解，check

• 存在多项式时间的验证算法

验证算法certifier 与证据certificate

• certificate 证书 证据 理解为instance s 的一个可能解t
• certifier C(s,t) check 可能解t是否满足问题X的一系列约束，返回yes 或者no
• C(s,t) =yes iff $s\in X$

举个例子：问题 X 二元一次方程是否有解，s 是一个二元一次方程，t（certificate）是一个可能的解，certifier 验证t能否使方程成立。

1.5 EXP问题

• 存在指数时间算法的判定问题。

$$P\subseteq NP\subseteq EXP$$
证明也很显然，P问题的多项式时间算法作为NP的验证算法，遍历NP问题的所有t（certificate）是指数时间。

2 Reduction 规约

常提到规约一般是多项式规约。
问题$X{\le }_{p}Y$

• 针对X的实例x，可以构造一个Y的实例y
• x $\in$ X, iff y $\in$ Y,看前面定义，这里$\in$意味着返回值为yes

3 NPC NP-完全问题

• NPC是NP问题
• 所有的NP问题可以规约为NPC问题
• P=NP iff NPC问题可解
  是否存在天然的NPC问题？ Circuit Satisfiability

3.0 Circuit Satisfiability 电路可满足性

给定一个由或与非组成的电路，固定一部分输入（hard-code input），是否存在输入使得output为1。

• 该问题显然为NP问题，因为存在多项式时间验证算法，直接带入输入计算结果即可
• 对于任意一个NP问题$X$，存在一个验证算法certifier C(s,t)。要判断是否有$s\in X$,such that C(s,t)=yes。
• 我们将s作为hard-coded input。将t作为input 构建一个Circuit Satisfiability 实例 y。设计电路等价该certifier。
• y is yes iff s is yes.

Circuit Satisfiability是一个天然的NPC问题。

3.1 3-SAT

• Literal 文字 ：一个布尔变量x或者它的否 $x_i$ or $\neg x_i$
• Clause 字句： 文字的disjunction（析取）（中文翻译感觉很离谱） $C_i=x_1\vee x_2\vee \neg x_3$
• Conjunctive normal form合取范式: $\Phi =C_1\wedge C_2\wedge C_3$
• SAT: Given CNF formula $\Phi$, does it have a satisfying truth assignment。给变量赋值，是的$\Phi$为真。
• 3-SAT: SAT where each clause contains exactly 3 literals。 每个字句有三个文字。
  

证明3-SAT是NPC问题。(CIRCUIT-SAT${\le }_p$ 3-SAT)

• 该问题显然是存在多项式时间的验证算法，因此是NP问题。

• 

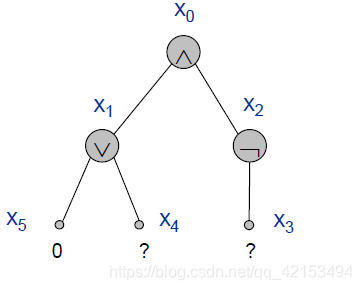
• 将CIRCUIT-SAT${\le }_p$ 3-SAT，电路中的或与非，等价的转化为一个或者多个字句都为真。
  $\neg$,$x_2=\neg x_3$等价于$x_2\vee x_3$, $\neg x_2\vee \neg x_3$均为真
  $\vee$,$x_1=x_4\vee x_5$等价于$x_1\vee \neg x_4$,$x_1\vee \neg x_5$,$\neg x_5\vee x_4\vee x_5$均为真
  $\wedge$,等价于$\neg x_0\vee x_1$,$\neg x_0\vee x_2$,$x_0\vee \neg x_1\vee \neg x_2$均为真。
  非常的巧妙，电路的每个操作都可以转化为多个子句为真。

• 对于hard-coded $x_5=0$等价于$\neg x_5$为真，$x_0=1$等价于$x_0$为真

• 将小于三个文字的子句等价的转化为三个文字的子句，如何转化？
  
  引入四个变量，保证由着四个变量组成得一些子句全为真时，其中两个一定为零。然后将这两个零变量加入只有一个文字的子句以及多个文字的子句。

• 上述两个例子的实例一个为真可以推出另一个为真。

3.2 Covering problems and Packing problems

3.2.1 indenpendent set 独立集

• Given $G(V,E)$ and integer $K$
• $S\subseteq V$,such that $|S|\ge K$ and for each edge at most one of its endpoints is in $S$。对于每条边，最多有一个点在$S$中。
• 判断是否存在$S$。是否存在大于$K$的点，使得这些点独立（点之间没有边）。
  

3.2.2 vertex cover 点集覆盖

• Given $G(V,E)$ and integer $K$
• $S\subseteq V$,such that $|S|\le K$ and and for each edge, at least one of its endpoints is in $S$。对于每条边至少有一个点在$S$中。
• 判断是否存在$S$。是否存在小于$K$个点覆盖（只要有一个点在$S$中即可）所有边。
  

3.2.3 set cover 集合覆盖

• Given a set U, a collection $S_1,S_2\dots ,S_n$ and a integer $k$
• Does there exist a collection of $\le k$ these whose union is equal to $U$?
• 判断是否存在小于$k$个子集$S_i$的并，等价于U。
  

3.3 Sequencing problems

3.3.1 Directed Hamiltonian Cycle 有向汉密尔顿环

• Given diggraph $G(V,E)$
• Does there exist a simple cycle $\Gamma$ contians every node in $V$
• 判定是否存在简单环$\Gamma$ 包含所有点。简单环：所有点只经过一次。

3.3.2 Hamiltonian Cycle 汉密尔顿环

• Given graph $G(V,E)$
• Does there exist a simple cycle $\Gamma$ contians every node in $V$
• 判定是否存在简单环$\Gamma$ 包含所有点。简单环：所有点只经过一次。
  

3.3.3 Traveling Salesperson Problem 旅行商问题

• Given n cities and a pairwise distance d(u,v)。
• Is there a tour of length $\le D$
• 判断是否有个tour(经过所有城市并且返回), 长度小于$D$。
  

3.4 Partitioning problems

3.4.1 graph 3-color 3色问题

• Given a undirected graph G
• exist a way to color the nodes RGB so that no adjacent nodes have the same color.
• 判断对这个无向图是否存在一种涂色，只用三个颜色，使得相邻节点颜色不同。
  

3.4.2 3D-MATCHING 3维匹配

• Given disjoint sets $X,Y$and $Z$。Each of size $n$ and a set $T\subseteq X\times Y\times Z$。
• Is there a set of $n$ triples in T, such that each element of $X\cup Y\cup Z$ is in exactly one of these triples。
• 判断是否存在$n$个元组,使得 $X\cup Y\cup Z$的元素都被包含一次。
  

3.5 Numerical problems

3.5.1 SUBSET-SUM 子集求和

• Given natural numbers $w_1,\dots ,w_n$ and integer $W$
• Is there a subset that adds up to exactly W?
• 判定是否存在一个子集使得求和为W
  

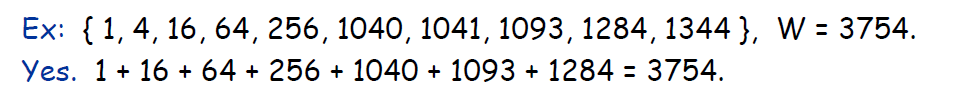
3.5.2 SCHEDULING 调度

• Given a set of $n$ jobs with processing time $t_i$, release time $r_i$, and deadline $d_i$。
• Is it possible to schedule all jobs on a single machine such that job $i$ is processed with a contiguous slot of $t_i$time units in the interval $[r_i,d_i]$ 即工作i一发布就做。
• 判断是否是否能完成所有工作，并且工作$i$的处理时间已经规定。
  

3.6 总结

下图问题全为NPC问题

$A{\le }_{p}B$将A规约为B，将A转为的B的形式求解。

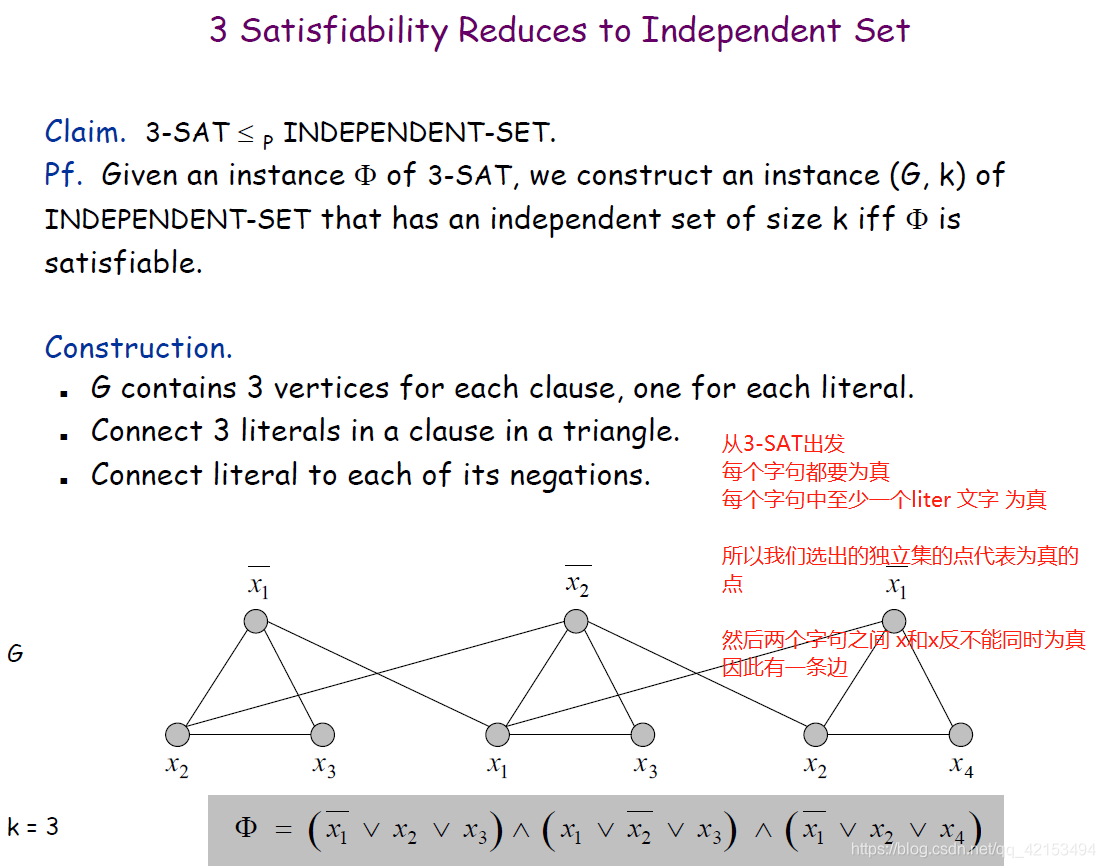
3.6.1 3-SAT ${\equiv }_P$ Independent Set将 3-SAT规约为独立集

• 给出3-SAT的实例$\Phi$,构造出独立集的实例，如下图所示，选出的节点为真
• 两者为真等价
• 

3.6.2 Vertex cover ${\equiv }_P$ Independent set 点集覆盖多项式等价与独立集

证明 S 是Independent set当且仅当V-S是vertex cover

• 任意一条边，一定存在一点不在S中，则一定有一点在V-S中。
• S中任意两个点一定不是一条边，即V-S外任意两点不存在边。
• 

3.6.3 Vertex Cover Reduces to Set Cover 点集覆盖规约为集合覆盖

给定一个Vertex Cover的实例 G=(V,E),k,将其构造为 Set Cover的实例(U,S,k)

• U=E,k=k, S v = { e ∈ E : e incident to v } S_v=\{e\in E:\text{e incident to v}\} Sv​={e∈E:e incident to v} 每个点有一个子集，子集元素为与改点相连的边。
• Set-cover of size $\le$k iff vertex cover of size $\le$k
• 

3.6.4 3-SAT${\le }_P$ Dir-Ham-Cycle将3-SAT规约为有向哈密尔顿环

• 给定一个3-SAT的实例，构造为有向哈密尔顿环，设计节点以及边。
• 文字由方向决定真假，字句由是否访问决定真假。
  

3.6.5 Dir-Ham-Cycle ${\le }_p$ Ham-cycle 有向哈密尔顿图规约到无向

通过添加节点以及一个节点只能经过一次来控制方向。

• G有解则G’有解
• G’有解则顺序固定 B, G, R,或者B, R, G,则G有解

3.6.6 Ham-cycle ${\le }_p$ TSP 哈密尔顿图规约到旅行商

Ham-cycle没有权重，TSP问题有权重以及距离限制。

只需要设置不同权重即可区分。

3.6.7 3-SAT${\le }_P$ 3-color 3-SAT规约为3色问题

• 给定3-SAT实例，构造G(V,E)，对文字以及字句分别构造。
• 
• 

3.6.8 3-SAT${\le }_P$ SUBSET-SUM 3-SAT规约为子集求和问题

• 通过设定求和的值来判断是否SAT。
  

3.6.9 SUBSET-SUM${\le }_P$ Scheduling 子集求和规约为规划问题

• 设定W的值即可。
  

4 co-NP与NPC

• co-NP：NP问题的补问题。

• 

• 

• 

• 一个例子

• 
  

• 

• 所有NP问题可以规约为NPC问题。

• 所有问题可以规约为NP-hard问题