线性代数基本定理1

---

1.中心主题

线性代数讲的是向量空间的线性变换。将一个子空间映射到另一个子空间。
特征值分解，Jordan标准型都是在寻找向量空间中的不变子空间。我们要在线性变换中寻找不变的量。

2.定理描述

秩-零度定理（rank-nullity theorem）

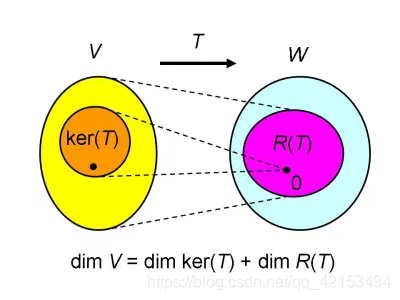
将上图转为矩阵语言：
矩阵$A\in R^{m\ast n}$，将一个n维空间映射到一个m维空间。

n=dim(R(A))+dim(N(A))
R(A)表示{y|y=Ax} A的值域空间 或者 A的列空间 (矩阵乘法为不同列的线性组合） 
N(A)表示{x|Ax=0} A的零空间

该定理表示经过映射，N(A)空间中的向量映射到0，剩下的向量映射到R(A)。
注:dim(R(A))<=m

3.证明

使用初等行变换，将矩阵$A$化简为简约行梯形式$R$（reduced row echelon form）。将其分块表达为
$$\begin{array}{c}R=\left[\begin{array}{cc}{I}_r& F\\ 0& 0\end{array}\right]\end{array}$$
初等行变换不改变零空间以及列空间维数，因为行换等价于乘一个可逆对角阵。
因此rank$A$=rank$R$=r,N($A$)=N($R$)=n-r