【算法系列02】分治法

最新推荐文章于 2023-11-02 16:51:20 发布

世界划水锦标赛冠军

最新推荐文章于 2023-11-02 16:51:20 发布

阅读量250

点赞数

本文链接：https://blog.youkuaiyun.com/qq_41898761/article/details/103836493

版权

本文介绍了分治法的思想和应用场景。分治法通过将问题分解为独立的子问题求解，常见应用包括求最大最小元、二分搜索、排序问题（如合并排序）和选择问题。在求解过程中，子问题不断缩小直至可以直接解决，最后合并子问题得到原问题的解。文章详细阐述了这些方法的具体步骤和策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、分治法思想：

1.原问题能分解成若干个小的问题，小的问题之间相互独立，且问题的类型相同。

2.子问题足够小的时候可以直接求解。

3.子问题的解能够合成原问题的解

因此多为递归问题。

二、应用

1.求最大最小元

求一组序列的最大最小元，能把长的序列分成两段短的序列。分别求出两段序列的最大值和最小值，再进行比较后合成整个序列的最大值和最小值。
极限就是分到最后序列就剩一个元素或者两个元素了，就可以直接得出最大值和最小值再向上合并。

#include <bits/stdc++.h>
using namespace std;
int L[100];
int n;
int MAX(int a,int b){return a>b?a:b;}
int MIN(int a,int b){return a>b?b:a;}

//函数无法返回两个值就在一起就行打包了
typedef struct
{
    int max;
    int min;
}T;

//关键代码
T MAXMIN(int i,int j)
{
    if(i==j)//序列只剩下一个元素
    {
        T t;
        t.max=t.min=L[i];
        return t;
    }
    else if(i+1==j)//序列剩下两个元素
    {
        T t;
        t.max=MAX(L[i],L[j]);
        t.min=MIN(L[i],L[j]);
        return t;
    }
        else//序列长度大于2继续分割序列
        {
            T t;
            //递归方程
            t.max=MAX(MAXMIN(i,(i+j)/2).max,MAXMIN((i+j)/2+1,j).max );
            t.min=MIN(MAXMIN(i,(i+j)/2).min,MAXMIN((i+j)/2+1,j).min );
            return t;
        }
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>L[i];
    T t=MAXMIN(0,n-1);
	cout<<t.max<<"  "<<t.min<<endl;
    return 0;
}

2.二分搜索

在有序表下求解给定关键字值的位置。
对半搜索，这个分界点为中间值m，m于给定值进行比较确定大致范围，逐渐缩小范围减小对比量。

#include <bits/stdc++.h>
using namespace std;

int L[100];

Bseach(int x,int left,int right)
{
    int m=(left+right)/2;
    if(x==L[m]) return m;
    else if(x>L[m]) return Bseach(x,m+1,right);
    else return Bseach(x,left,m-1);
}

int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>L[i];
    int x;
    cin>>x;
    cout<<Bseach(x,0,n-1)<<endl;
    return 0;
}

3.排序问题

合并排序
将序列一分为二，进行排序然后把排序好的序列进行合并。一般分治法会把序列分的只剩长度为一的。问题足够小时就是序列为空或者只有一个元素。
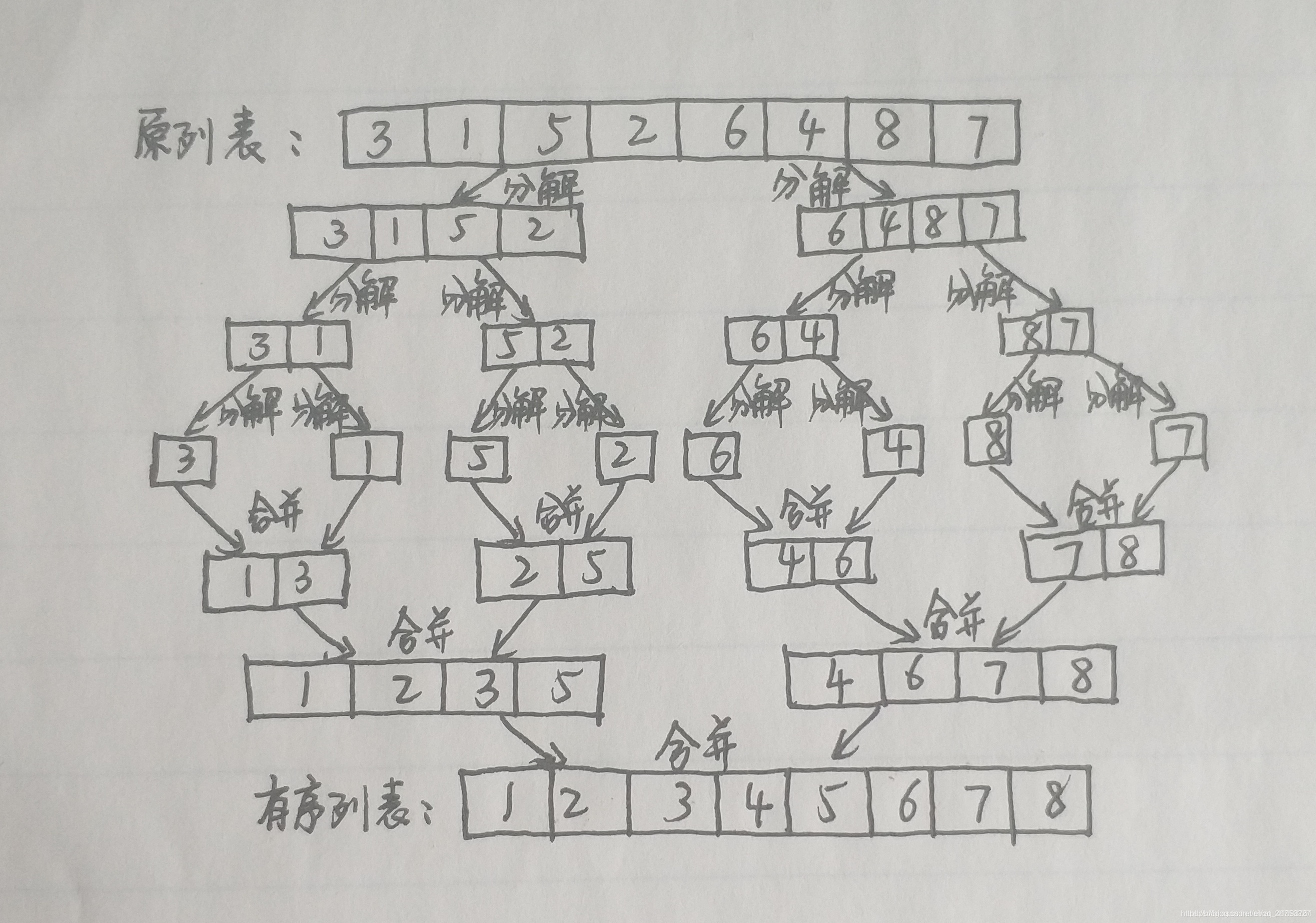
在这里插入图片描述
(1)、分解，递归分解，求解
3 1 5 2 6 4 8 7

void MergeSort(int Array[], int begin, int end){
	
	if(begin + 1 < end){  //将一个长的序列分解为，只含有一个元素的数组。 		 
		int middle = (end + begin) / 2;  
		MergeSort(Array, begin, middle);  //归并前半个数组
		MergeSort(Array, middle+1, end);  //归并后半个数组
		//把两部分排序好的放进去进行合成如：传入1325进行排序
		Merge(Array, begin, middle, end);  //讲两个数组合并
	}
}

(2)、合并。
思路是先比较两个序列（此处是把两个序列连起来以后传入的但思路一样）依次比较最小的，然后当一个序列空的时候把另一个序列全部输入进去

void Merge(int Array[], int begin, int middle, int end){
	int n1 = middle - begin;
	int n2 = end - middle;
	
	int *left = new int[n1];
	int *right = new int[n2];
	
	for(int i = 0; i < n1; i++)
		left[i] = Array[begin + i];    
	for(int i = 0; i < n2; i++)
		right[i] = Array[middle + i];  
	
 
	int i = 0, j = 0, key;
	for(key = begin; key < end; key++){
		if(i < n1 && left[i] <= right[j])
			Array[key] = left[i++];
		
		else if(j < n2 && left[i] >= right[j])
			Array[key] = right[j++];
		
		else if(i == n1 && j < n2){
			Array[key] = right[j++];
		}
			
		else if(j == n2 && i < n1){
			Array[key] = left[i++];
		}	
			
	}
}

C++传入数组其实就是传入指针
将原数组分成只含有一个的时候到一个元素的时候if已经进不去了，就返回上一层执行合并函数Merge。
划分完从下到上进行合并排序

快速排序
划分完从上到下进行合并
划分到最小都是序列为空或者是序列只有一个元素

#include <bits/stdc++.h>
using namespace std;

int fenhua(int L[],int left,int right)
{
    int i=left;
    int j=right+1;
    do{
        do i++;while(L[i]<L[left]);
        do j--;while(L[j]>L[left]);
        if(i<j)
        {
            int temp=L[i];
            L[i]=L[j];
            L[j]=temp;
        }
    }while(i<j);
    int temp=L[left];
    L[left]=L[j];
    L[j]=temp;
    return j;
}

void QuickSort(int L[],int left,int right)
{
    if(left<right)
    {
        int j=fenhua(L,left,right);
        cout<<j<<endl;
        QuickSort(L,left,j-1);
        QuickSort(L,j+1,right);
    }
}
int main()
{
    int n;
    cin>>n;
    int L[100];
    for(int i=0;i<n;i++)
        cin>>L[i];
    QuickSort(L,0,n-1);
    for(int i=0;i<n;i++)
        cout<<L[i]<<" ";
    return 0;
}