【算法系列03】贪心算法

一、贪心算法思想

贪心算法目的是求解最优化问题。

遵循贪心准则：当前步骤中所有可行选择中最佳的局部选择。

• 贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。

二、应用

1.背包问题

单位重量价值最高的物品优先装包。
先计算单位价值
排序
依次装包

#include <bits/stdc++.h>
using namespace std;
struct GOODS
{
    int weight;
    int value;
    double valpeiwei;
    double load;
} ;

int cmp( GOODS const &a, GOODS const &b)//定义sort函数的比较函数
{
    if(a.valpeiwei<b.valpeiwei) return 0;
    else return 1;
}

void Greedy(GOODS G[],int num,int bagvol)
{
    for(int i=0;i<num;i++)
    {
        if(bagvol>G[i].weight)
        {
            G[i].load=1;
            bagvol-=G[i].weight;
        }
        else if(bagvol>0)
        {
            G[i].load=(double)bagvol/G[i].weight;
            bagvol=0;
            return;
        }
    }
}

int main()
{
    //题设要求
    int total_num=0,total_weight=0;
    //背包初始化
    int num;
    cin>>num;
    int bagvol;
    cin>>bagvol;
    GOODS G[num];
    for(int i=0;i<num;i++)
    {
        cin>>G[i].weight>>G[i].value;
        G[i].valpeiwei=(double)G[i].value/G[i].weight;
        G[i].load=0;
    }
    //就性价比进行排序
    sort(G,G+num+1,cmp);
    //调用贪心算法开始装包
    Greedy(G,num,bagvol);
    //就装包结果开始分析
    for(int i=0;i<num;i++)
    {
        if(G[i].load==0) break;
        total_num+=(G[i].value*G[i].load);
        total_weight+=(G[i].weight*G[i].load);
    }
    cout<<total_num<<" "<<total_weight<<endl;
    return 0;
}

2.带时限的作业排序

3.单源最短路径（迪杰斯特拉算法）

指定一个点到其余各个点的最短路径
思想：顶点集S的贪婪扩充，通过边来松弛1号点到其余各个点的路程

图中最优距离的问题
首先要把图表示出来-----邻阶矩阵

需要一个记录路程的数组dis[ ];

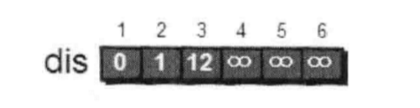
这里表示的是一号点到其余点的最短距离。此时数组里的数值为最短距离的估计值。

首先我们先选择离一号点最近的点，也就是二号点。选择二号点后dis[2]就从估计值变成了确定值。（不存在通过第三边使得一号和二号点距离变得更近）

选择了2号顶点以后，便把一二号边引入了，现在考虑通过这个边是否能松弛一号到其他点的距离呢（从出边考虑）。如dis[3] 于 dis[2]+e[2][3]进行比较

然后在更新完dis[ ]后，选择到1号点最近的顶点，把估计值变成确定值，这个顶点加入了S的行列。

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int e[20][20];//边于边的距离，邻接矩阵
    int dis[20];//记录最短路径
    int book[20];//记录该节点是否已经确定并且加入了S，加入了用1，否则用0
    int inf=99999999;//定义无限大
    int u;
    int n,m;
    cout<<"输入顶点个数和边条数"<<endl;
    cin>>n>>m;

    //初始化邻接矩阵,dis[]和book[]
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j) e[i][j]=0;
            else e[i][j]=inf;
    for(int i=1;i<=n;i++)
    {
        dis[i]=e[1][i];
        book[i]=0;
    }
    book[1]=1;
    
    //读入边
    for(int s=1;s<=n;s++)
    {
        int t1,t2,t3;
        cin>>t1>>t2>>t3;
        e[t1][t2]=t3;
    }

    //迪杰斯特拉核心算法
    for(int i=1;i<=n;i++)
    {
        int min=inf;
        for(int j=1;j<=n;j++)
        {
            if(book[j]==0&&dis[j]<min)
            {
                min=dis[j];
                u=j;
            }
        }
        book[u]=1;
        for(int v=1;v<=n;v++)
        {
            if(e[u][v]<inf)
            {
                if(dis[v]>dis[u]+e[u][v])
                    dis[v]=dis[u]+e[u][v];
            }

        }
    }

    for(int i=1;i<=n;i++)
        cout<<dis[i]<<" ";


    return 0;
}