PP4FPGA--Chapter4 离散傅里叶变换_基于fpga的数字信号处理基4抽取的傅里叶变换-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_41645695/article/details/120967397

1 傅里叶级数

Discrete Fourier Transformation, DFT. 离散傅里叶变换的核心是以一组固定系数执行矩阵向量乘法。傅里叶级数提供了一种方法来观察从-Π到Π的一个周期内的连续实值周期信号。

Jean Baptiste Joseph Fourier的开创成果表明，在2Π周期内任何连续的周期性信号都可以用周期为2Π的余弦和正弦和表示。

2 DFT背景介绍

离散傅里叶级数对于周期连续性信号的作用可以通过对离散傅里叶级数的推倒得以证明，而离散傅里叶变换是针对于离散的周期信号。DFT可以将有限数量的等间隔样本转换成有限数量的复数正弦曲线。即将一个采样函数从一个域（时域）转换到频域。

信号在时频域之间的转换有什么作用？

在数字通信中，要将模拟信号采样后进行传输。但在时域上，即使采样周期再密集也无法唯一的还原出原始信号。就是说，采样信号是离散的，在时域上不会无时无刻连续的进行数据的采集，也就是说在时间上会有间隔，时间上采集的信号不是持续不断地，是离散的，在某个时间点采集到某个数据。那么如此来讲，时域上的信息量就会有所损失。然而在频域上来看，经过采样的信号为原始信号在频域上的搬移及累加，就是说，在频域上来讲，频域上的信号是周期性的吗？若采样方式满足抽样定理就是采样频率为原始信号最高频率的二倍（过采样），就可以通过低通滤波器获得原始信号的基带频域。再利用傅里叶逆变换获得原始信号。由此可见一个采样后信息量有损失的信号可以通过傅里叶变化，低通滤波器滤波整形，傅里叶逆变换这样的方式完整的恢复。这就是时频变化的作用。

离散信号和周期信号的关联在于它可以用一组有限的数字表示。

//实现矩阵向量乘法的代码
#define SIZE 8
typedef int BaseType;

void matrix_vector(BaseType M[SIZE][SIZE], BaseType V_In[SIZE], BaseType V_Out[SIZE]){
	BaseType i,j;
data_loop:
	for(i=0; i<SIZE; i++){
		BaseType sum=0;
	dot_product_loop:
		for(j=0;j<SIZE;j++){
			sum+=V_In[j]*M[i][j];
		}
		V_Out[i]=sum;
	}
}

3 矩阵向量乘法的优化

整体策略概括：先在算法中展开循环，然后在HLS中设置算法间隔数，利用流水线将顺序操作改成并行执行以提升数据处理的效率。

矩阵向量是DFT计算的核心，输入的时域向量乘以一个固定特殊值的矩阵，输出的结果是与输入时域信号相对应的频域矢量。

这里我们将M=S和V_In设置为采样的时域信号，Vout将包含DFT。SIZE是决定输入信号中样本数量的常数，也决定了DFT的大小。

在我们写的一个循环标记dot_product_loop，标志着这个算法的核心计算即一个嵌套的for循环。循环量是从0-SIZE计算DFT的系数。针对这个循环，在HLS中，首先，应该考虑在希望综合成什么样的结构体系。这个问题可以具体归结为：你想把代码中的数据存储到哪里？因为将变量映射到硬件时有诸多选项。该变量可能只是一组电线（如果该变量的值不需要在一个周期内保存）、寄存器、RAM或FIFO。但所有这些选项都需要在速度和面积之间做折中的选择。其次，需要考虑的重要因素是代码并行度的可用性。

4 流水线和并行运行

在矩阵乘法中，可以很大程度上利用并行思想解决问题。首先关注每次迭代循环执行的内部循环表达式sum+=Vin[j] *M[i][j].乘法运行时，计数变量SUM在每次迭代中都被重复利用并赋予新的值。这个内部循环可以重新表述，消除变量SUM，手动展开矩阵向量乘法内部循环实例，并在较大表达式中替换为多个中间值。

#define SIZE 8
typedef int BaseType;

void matrix_vector(BaseType M[SIZE][SIZE], BaseType V_In[SIZE], BaseType V_Out[SIZE]){
    BaseType i, j;
data_loop:
    for(i=0;i<SIZE;i++){
        BaseType sum=0;
        V_Out[i] = V_In[0]*M[i][0]+V_In[1]*M[i][1]+V_In[2]*M[i][2]+V_In[3]*M[i][3]+V_In[4]*M[i][5]+V_In[5]*M[i][5]+V_In[6]*M[i][6]+V_In[7]*M[i][7];
    }
}

循环的展开可以由VivadoHLS在流水线中自动执行，也可以通过使用#pragma HLS unroll 或者流水线外的等价指令来实现。

替换内部循环的新表达式应该具有大量的并行性。如此而来每个乘法可以并行执行，而且可以使用加法器树来执行求和。

如果我们希望展开内循环的表达式的任务延迟最小，那么所有的八个乘法运算都应该并行执行。假设乘法延迟3个周期，加法延迟1个周期，则整个流程有6个周期的延迟。所有的V_In[j]*M[i][j]草操作在第三周期结束时完成。使用加法器树对这八个中间结果求和还需要再来3个周期。

需要注意的是，在FPGA中加法器通常是无法共享的，因为加法器和多路复用器需要相同数量的FPGA资源。如果不使用8个乘法器，则可以增加执行该功能的周期数量来减少资源使用量。换句话说，为了使用更少的乘法器，我们需要牺牲更多的时间周期来完成内部循环。

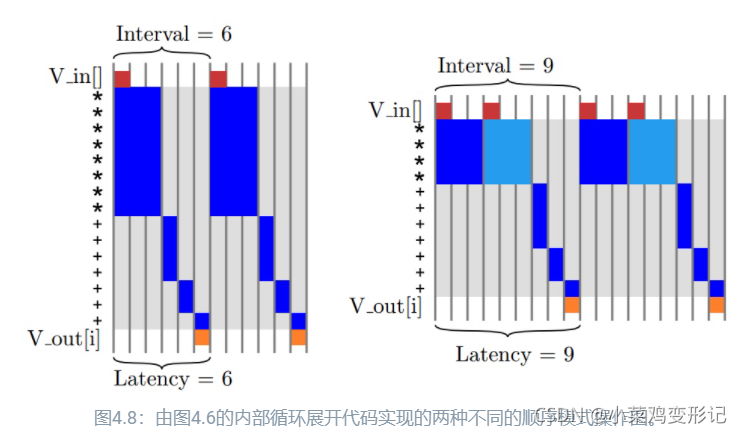
从该图中，可以明显看出有许多重要时间段并没有执行有效的工作，因而降低了设计的总体效率。其实，data_loop每次的迭代实际上是完全独立的，这意味着它们可以同时执行。如展开dot_product_loop一样，也可以展开数据循环并同时执行所有的乘法运算，但这需要大量的FPGA资源。其次，更好的选择是尽快启动循环的每次迭代，意味着前一次循环仍在执行。这个过程被称为循环流水线化，通过#pragma HLS pipeline 在Vivado HLS中实现。循环流水线在大多数情况下可以减少循环的间隔时间，但不会影响延迟时间。

充分利用流水线乘法器的优势：

可以在不添加额外运算符的前提下减少内部循环的延迟。如下图，左侧，使用了三个流水线乘法器，在这种情况下，乘法操作可以并发执行因为乘法操作是独立进行的没有依赖性，而加法操作只有在第一次乘法完成之后才能开始。在右图中通过设置#pragma HLS pipeline II=3，应用于data_loop则与Vivado HLS的结果类似。这样不仅个别操作在同一个操作符上并发执行，而且这些操作可能来自于不同的data_loop迭代。

我们可以在不同的层析级别上进行流水线操作，包括算法、循环、功能级别。此外，不同级别的流水线在很大程度上也是独立的。可以在顺序循环中使用流水线操作符，或者可以使用顺序操作符来构建流水线循环，也可以构建大型功能的流水线实现。

5 存储权衡和数据分区

数据的存储位置对整个处理器的性能和资源使用情况有重要影响。在大多数处理器系统中，内存架构是固定的，因此只能调整程序以最大程度地利用可用地内存层次结构。在HLS设计中，可以利用不同地存储器结构，并尝试找到最适合特定算法地存储器结构。

通常，大量数据存储在片外存储器如DRAM，闪存或网络连接地存储器中，但是数据访问时间通常很长。由于大量地电流必须通过长电线访问片外存储器，所以使用片外存储器消耗地能量也比较大。相反，片上存储器可以快速访问并且功耗要低得多，只是它可以存储的数据量有限。有一种常见的操作模式类似于通过CPU的内存层次结构中的缓存效果，它是将数据重复地加载到块中地片上存储器上。

当我们选择片上存储器时，需要在嵌入式存储器如Block RAM或触发器FF之间权衡。

基于触发器的存储器FF允许在一个时钟内对不同地址地数据进行多次读取，也可以在一个时钟周期内读取、修改和写入基于触发器的存储器。FF的数量通常限制在10万字节左右，甚至更小。

Block RAM，BRAM提供更高的容量，拥有Mbytes的存储量，其代价是有限的可访问性。例如，单个BRAM可以存储大于1到4千字节的数据，但是在每个时钟周期只可以对该数据的两个不同的地址进行访问。此外，BRAM需要尽可能减少流水线操作。

对于二者的权衡选择方向：如果说数据的吞吐量是我们需要考虑的最重要的问题，则所有数据都将存储在FF中。这将允许任何元素在每个时钟周期内被访问尽可能多的次数。但当计算产生的数据量较大需要更多的存储空间时，即使使用BRAM也需要很多个块。另一方面，使用单个大型基于BRAM的内存意味着我们一次只能访问2个元素，降低了性能。

在实际中，大多数设计需要更大的阵列分布存放在更小的BRAM存储器中，这种方法被称为阵列分区。较小的数组可以完全划分为单独的标准变量并映射到FF。匹配流水线选择和数组分区以最大限度地提高运算符使用率和内存使用率是HLS设计探索地一大方面。

下面探究变化地流水线和阵列分区对性能和面积地影响。

通过流水线操作并将部分循环展开应用于dot_product_loop，使用这种方式循环展开后，对应原始的循环迭代，HLS可以并行地在两个表达式中实现这些操作。如果没有适当的数组分区，可展开内部循环可能不会提高性能。因为并发读取操作的数量受到内存端口数量的限制。可以将一次循环中用到的不同数据存放在不同的BRAM中，以并行执行、运算、循环后面的数据。

【HLS工具可以使用unroll指令自动展开循环。该指令使用一个因子作为参数，为正整数类型，表示循环体应该展开的次数。】

使用array_partition cyclic factor=2指令和将M[][]和向量V_In[]手动划分为单独的数组有着相同的效果。

同时执行数组分区和循环展开的代码之间的性能结果有什么不同？使用指令执行数组分割和循环展开的结果与手动执行的结果相比有何不同？

数组分区通常与流水线操作并行执行。通过两倍的数组分割可以使性能提高2倍。可以通过2倍的数组分割或者外部循环数减小一半来实现。提升性能需要相应数量的阵列分区。一般情况下，将性能提高2倍将使用大约两倍的资源，相反将性能降低2倍可以节约一半的资源。

6 Baseline实现

解决两个问题：第一，浮点运算产生的较大延迟；第二，大型矩阵的存储问题。

处理大量复杂数字的能力是需要重点考虑因素之一。浮点运算符特别是加法运算符比整数加法具有更大的延迟。第二个变化是我们希望能够将设计容量扩展到一个大输入矢量的大小，比如N=1024个输入样本。

首先要有一个保证它具有正确的功能baseline基线代码。通常这些代码都以非常连续化的方式运行；它没有高度优化，因此可能无法达到所需要的性能指标。实现浮点运算尤其是双精度浮点运算通常代价很高并且需要很多流水线操作。但通过流水线操作，这些高延迟操作的影响便不那么重要，因为可以同时执行多个循环执行。

一种方法是降低计算的精度。这种方法在实际应用中是有价值的，因为它减少了每个操作所需资源，减少了存储值所需的内存，并且也减少了操作的延迟。

另一种方法是可以用一种与矩阵向量乘法非常相似的技术即复制只读的数组的存储。

由于在任意给定的周期，我们只能获取其中一个阵列的一个数据，这可能会在函数中并行的乘法和加法运算方面产生瓶颈。这就是为什么必须将所有的输出结果存储在一个临时数组的原因。然后将所有这些结果复制到函数结尾处的sample数组中。

8 总结