leetcode96——不同的二叉搜索树——java实现

题目要求：

分析：
首先看看什么叫二叉搜索树。百度百科是这样定义的：
所以左子树的所有值都比根节点要小，右子树的所有值都比根节点要大。

这里要求1,2,…,n的二叉搜索树有多少种，我们这样来考虑：
假设在1,2,…,n中，我们取第nums[i]个作为根节点，那么i个数（1 ~ i - 1，再加上一个空树的情况）全都比nums[i]要小，后面n - i - 1个数全都比nums[i]要大；

而查找不同形态的二叉搜索树的个数是满足Catalan数的，这个是数学上的一个式子，不去深究，但是二叉搜索树的个数 = 左子树的个数 * 右子树的个数（可以理解为左边所有情况 * 右边所有情况）；

那么根据二叉搜索树的要求，作为左子树的值肯定要比根节点的值要小，从nums[1] ~ nums[i - 1]对这些值进行遍历，让它们挨个作为左子树，其它的都作为右子树，然后将它们的值相乘就好了。

**注：**这里的nums的范围是nums[0] ~ nums[n]，因为也要判断没有数字的情况，此时为nums[0]，是一颗空树，所以可以认为只有一种排序方法，返回1.

举个例子可能比较好理解：

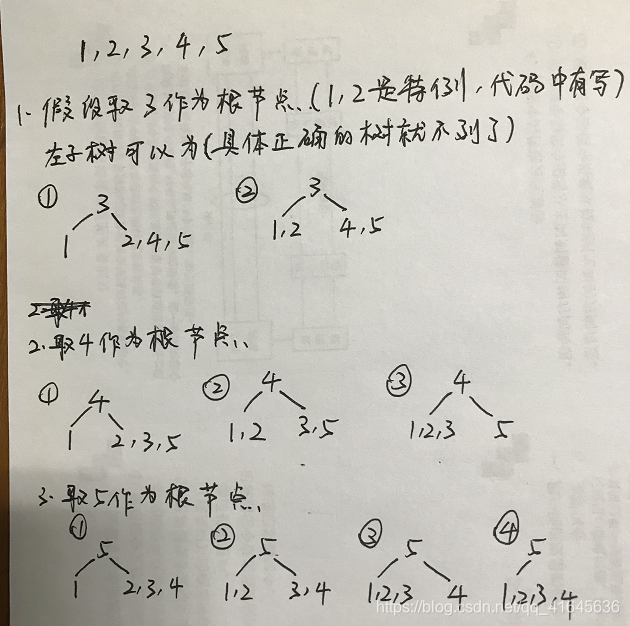
具体代码如下：

class Solution {
    public int numTrees(int n) {
        if(n == 0)
            return 0;
        if(n == 1)
            return 1;
        
        int[] nums = new int[n + 1];
        nums[0] = 1;
        nums[1] = 1;
        //取值，1和2是特殊情况，所以要从3开始取，对应的坐标是2
        for(int i = 2; i <= n; i ++) {
            //分左子树和右子树
            for(int j = 0; j < i; j ++) {
                nums[i] += nums[j] * nums[i - 1 - j];
            }
        }
        return nums[n];
    }
}