Prim算法详解

Prim算法是用来寻找一个联通图的最小生成树的算法，是数据结构中一个十分经典的算法，与他齐名的还有了克鲁斯卡尔算法，将会在下一篇
中提到。
Prim算法思想（归并顶点）：
首先给定一个起始点，例如我们以A为起始点，选择与它关联的具有最小权值的边，将其加入到生成树的集合顶点U中去（这里我们用visited[i] = true 来实现）；
然后我们进行N - 1次循环从U中 及 非U中选择两个联通的且具有最小权值的顶点，把非U的顶点加入U中，直到所有顶点都加入到U中为止。
实例图：

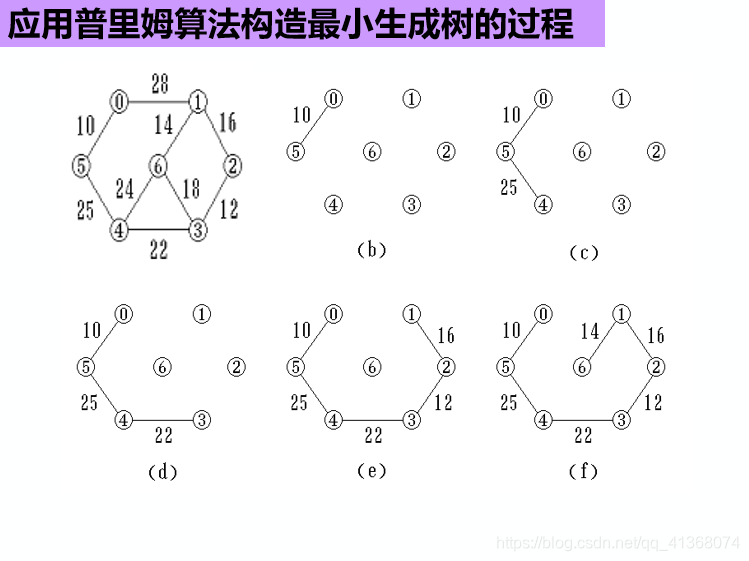
这个图较为清晰直观的分析了Prim算法的思想。
代码如下：
1.数据及结构的定义：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>

#define N 100
#define INITFITE 1000000
using namespace std;

struct Node{
	char data;
	int lowcost;
}closedge[N];

typedef struct NNode{
	int vernum,arcnum;//顶点数，边数；
	char ver[N];
	int martrix[N][N]; 
}Graph;

int locate (Graph G,char ch)  //找到对应字符的下标;
{
	int i;
	for (i = 0;i < G.vernum;i++)
	{
		if (G.ver[i] == ch)
		return i;
	}
}

2.建立邻接矩阵：

void create_Graph (Graph &G)
{
	char v1,v2;
	int weight; //权值；
	cout<<"please key in the vernum & arcnum"<<endl;
	cin>>G.vernum>>G.arcnum;
	cout<<"please key in all the vertexs"<<endl;
	for (int i = 0;i < G.vernum;i++)
	cin>>G.ver[i];
	cout<<"please key in the v1 & v2 & weight"<<endl;
	for (int ii = 0; ii < G.vernum;ii++)
	for (int jj = 0; jj < G.vernum;jj++)
	G.martrix[ii][jj] = INITFITE;   //初始化矩阵的时候将矩阵的值赋成无穷大。
	for (int ii = 0;ii < G.arcnum;ii++)
	{
		cin>>v1>>v2>>weight;
		int i = locate(G,v1);
		int j = locate(G,v2);
		//cout<<i<<" "<<j<<endl;
		G.martrix[i][j] = weight;
		G.martrix[j][i] = weight;
	}
}

3.Prim算法：

bool visited[N];

void Prim(Graph &G,char ch)
{
	int v,w;
	v = locate(G,ch);
	visited[v] = true;
	int min = 1000000;
	for (int i = 0;i < G.vernum;i++)//为第一个顶点找到邻接点
	{
		if (!visited[i]) 
		{	
			closedge[i].data = G.ver[v]; //将第i的点的上一个邻接点暂时赋成G.ver[v]；
			closedge[i].lowcost = G.martrix[v][i];
			if (closedge[i].lowcost < min)  //判断并找到最小的权值
			{
				min = closedge[i].lowcost;
				w = i;		//记录最小权值的下标
			}
		}
	}
	cout<<closedge[w].data<<" "<<G.ver[w]<<" "<<closedge[v].lowcost; //输出！！
	cout<<endl;
	//visited[w] = true;
	for (int i = 0;i < G.vernum - 2;i++)//n-1次循环找到剩余的n-1个点
	{
		visited[w] = true;//将G.ver[w]加入U；
		v = w;
		min = 1000000;
		for (int j = 0;j < G.vernum;j++)
		{
			if (!visited[j])
			{
				if (G.martrix[v][j] < closedge[j].lowcost) //关键（核心思想）：看G.ver[w]的引入是否改变了到达其他顶点的最小值，如果改变了就从新赋值，否则不变。
				{
					closedge[j].data = G.ver[v];
					closedge[j].lowcost = G.martrix[v][j];
				}
				if (closedge[j].lowcost < min)
				{
					min = closedge[j].lowcost;
					w = j;
				}
			}	
		}
		cout<<closedge[w].data<<" "<<G.ver[w]<<" "<<closedge[v].lowcost;
		cout<<endl;	
	}
}

4.主函数

int main(){
	Graph G;
	create_Graph(G);
	for (int i = 0; i < G.vernum;i++)
	{
		for (int j = 0; j < G.vernum;j++)
		printf("%8d",G.martrix[i][j]);
		cout<<endl;
	}
	Prim(G,'A');
	return 0;
}

Prim 算法在考研中占有相当大的比重，要求熟练掌握编码！！