机器学习线性回归。

线性回归

回归的理解

大自然让我们回归到一定的区间范围之内；反过来说就是，有一个平均的水平，可以让突出的事物能向他靠拢
从我们最熟悉的开始…线性方程

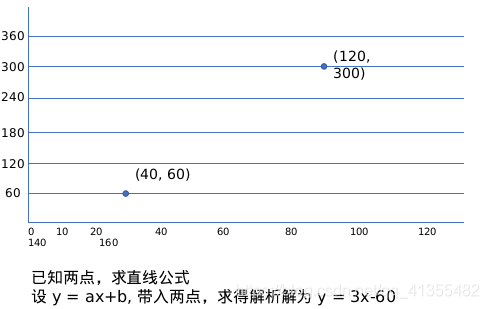
线性回归的一般步骤

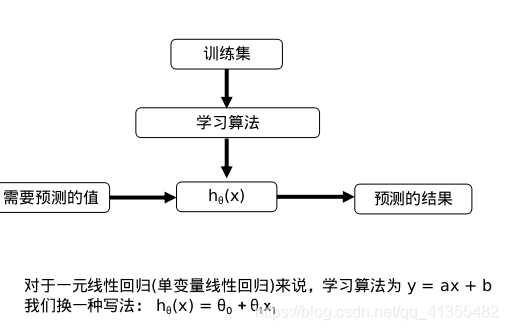
损失函数

损失（代价）函数 引入
线性回归实际上要做的事情就是： 选择合适的参数（w, b），使得f(x)方程，很好的拟合训练集。
模型：hθ(x) = θ0 + θ1x1
参数：θ0, θ1
损失函数：

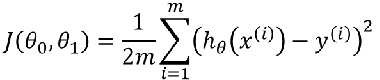
目标：最小化损失函数。j（θ0, θ1）

梯度下降

一、梯度法思想
梯度法思想的三要素：出发点、下降方向、下降步长。
机器学习目标函数，一般都是凸函数，什么叫凸函数？限于篇幅，我们不做很深的展开，在这儿我们做一个形象的比喻，凸函数求解问题，可以把目标损失函数想象成一口锅，来找到这个锅的锅底。非常直观的想法就是，我们沿着初始某个点的函数的梯度方向往下走（即梯度下降）。在这儿，我们再作个形象的类比，如果把这个走法类比为力，那么完整的三要素就是步长（走多少）、方向、出发点，这样形象的比喻，让我们对梯度问题的解决豁然开朗，出发点很重要，是初始化时重点要考虑的，而方向、步长就是关键。事实上不同梯度的不同就在于这两点的不同！
梯度下降的方向1：只要对损失函数求导，θ的变化方向永远趋近于损失函数的最小值。
梯度下降的方向2： 如果θ已经在最低点，那么梯度将不会发生变化。
不论斜率正或负，梯度下降都会逐渐趋向最小值。如果α太小的话，梯度下降会很慢。如果α太大的话，梯度下降越过最小值，不仅不会收敛，而且有可能发散。
线性回归的梯度下降 。

“Batch” Gradient Descent 批梯度下降：批梯度下降：指的是每下降一步，使用所有的训练集来计算梯度值。因此每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点，凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点，缺陷就是学习时间太长，消耗大量内存。
“Stochastic” Gradient Descent 随机梯度下降：随机梯度下降：指的是每下降一步，使用一条训练集来计算梯度值。
SGD的缺点在于每次更新可能并不会按照正确的方向进行，参数更新具有高方差，从而导致损失函数剧烈波动。不过，如果目标函数有盆地区域，SGD会使优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样对于非凸函数，可能最终收敛于一个较好的局部极值点，甚至全局极值点。
举个简单例子。

"""
随机梯度下降
"""
import numpy as np
import random
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]

n_epochs = 500
a0 = 0.1
decay_rate = 1

m = 100
num = [i for i in range(100)]

def learning_schedule(epoch_num):
    return (1 / (decay_rate * epoch_num + 1)) * a0
theta = np.random.randn(2, 1)

# epoch 是轮次的意思,意思是用m个样本做一轮迭代
for epoch in range(n_epochs):
    # 生成100个不重复的随机数
    rand = random.sample(num, 100)
    for i in range(m):
        random_index = rand[i]
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = xi.T.dot(xi.dot(theta)-yi)
        learning_rate = learning_schedule(epoch+1)
        theta = theta - learning_rate * gradients
print(theta)

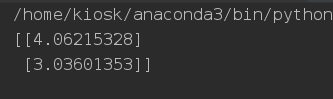
“Mini-Batch” Gradient Descent “Mini-Batch”梯度下降：“Mini-Batch”梯度下降：指的是每下降一步，使用一部分的训练集来计算梯度值。SGD相比BGD收敛速度快，然而，它也的缺点，那就是收敛时浮动，不稳定，在最优解附近波动，难以判断是否已经收敛。这时折中的算法小批量梯度下降法，MBGD就产生了，道理很简单，SGD太极端，一次一条，为何不多几条？MBGD就是用一次迭代多条数据的方法。我们同样是刚才的例子。

import numpy as np
import random

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]

n_epochs = 500
t0, t1 = 5, 50

m = 100
num = [i for i in range(100)]

def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2, 1)
batch_num = 5
batch_size = m // 5

for epoch in range(n_epochs):
    # 生成100个不重复的随机数
    for i in range(batch_num):
        start = i*batch_size
        end = (i+1)*batch_size
        xi = X_b[start:end]
        yi = y[start:end]
        gradients = 1/batch_size * xi.T.dot(xi.dot(theta)-yi)
        learning_rate = learning_schedule(epoch*m + i)
        theta = theta - learning_rate * gradients
print(theta)