LightOJ - 1282 Leading and Trailing 数论基础

题意:求n的k次方的前三位和后三位，后三位要补前导零。
思路：
后三位快速幂取模 模1000即可
前三位的话 ：
任何一个数都可以表示成 10^a的形式 a是可以是整数也可以是小数
n^k也不例外
我们可以推出 a

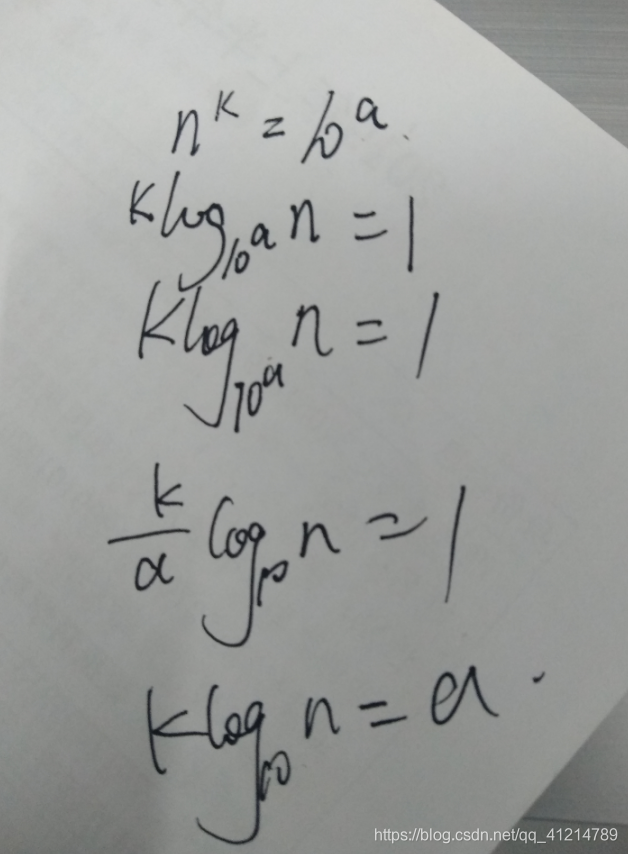
这里介绍一个可以对double型取模的函数 fmod()
这里就可以fmod(a,1) 即只要k的小数部分 再加上2
即fmod(k*log10(n),1)+2
再以10为底数进行幂运算，就是n^k的前三位
(
细说：
前三位，需要用到一个知识点，那就是给定一个数n，这个数可以表示成10^a，这个a一般是小数，那么n ^k就等于10 ^ak，这里把ak分为两部分，整数和小数部分，即x和y，那么n ^ k = 10 ^ x * 10 ^y，由于x是整数，那么很明显他是用来指定位数的，因为10 ^x肯定是一个10， 100， 10000…之类的数字，也就是说10 ^y才是这个数字的有效部分，我们只要求出10 ^y，然后乘上100最终结果就是我们想要的。
本段话引用自这里
)

#include<iostream>
#include<algorithm>
#include<string.h>
#include<map>
#include<queue>
#include<cmath>
#include<cstdio>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=105;
const int mod=1000;
int dp[maxn][maxn];
ll qmod(ll a,ll b)
{
	ll ans=1;
	while(b)
	{
		if(b&1)
			ans=(ans*a)%mod;
		b>>=1;
		a=(a*a)%mod;
	}
	return ans;
}
int main()
{
	int t;
	scanf("%d",&t);
	int ok=1;
	while(t--)
	{
		int n,k;
		scanf("%d%d",&n,&k);
		int ans=pow(10,fmod(k*log10(n),1)+2);
		printf("Case %d: %d %.3d\n",ok++,ans,qmod(n,k));
	}
	return 0;
}