LeetCode Day5

监控二叉树与坏计算器

最新推荐文章于 2024-02-04 17:20:34 发布

creep9709

最新推荐文章于 2024-02-04 17:20:34 发布

阅读量241

点赞数

CC 4.0 BY-SA版权

分类专栏：学习

本文链接：https://blog.youkuaiyun.com/qq_40676859/article/details/90244840

学习专栏收录该内容

9 篇文章

订阅专栏

本文探讨了两道算法题：一是计算监控二叉树所有节点所需最小摄像头数量的问题，通过递归策略实现；二是解决坏计算器从X达到Y的最小操作数问题，采用逆向思维优化算法。

968. 监控二叉树
难度：困难
给定一个二叉树，我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1：
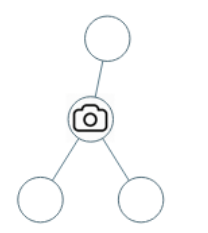
在这里插入图片描述

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：
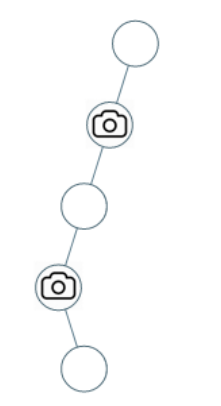
在这里插入图片描述

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

解：
执行用时 : 2 ms, 在Binary Tree Cameras的Java提交中击败了98.46% 的用户
内存消耗 : 35.7 MB, 在Binary Tree Cameras的Java提交中击败了100.00% 的用户
思路：递归，并且由下往上进行如下判断：
1.若节点没有左右节点，直接返回
2.若有子节点，如下判断
1 )若子节点存在0，则该节点设置为2(表示为摄像头)，并摄像头总数加1
2 )若子节点存在2，则该节点设置为-1(表示该点已经被摄像头覆盖到，不需要考虑)
3 )若该点为根节点且子节点不存在2，则根节点设置为2，摄像头总数加1
Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int cameras=0;
    public int minCameraCover(TreeNode root) {
        if(root.left==null&&root.right==null) //只有根节点，返回1
            return 1;
        setCameras(root,root); //递归
        return cameras;
    }
    public void setCameras(TreeNode root,TreeNode node) {
        if(node==null)
            return;
        if(node.left!=null)
        setCameras(root,node.left);
        if(node.right!=null);
        setCameras(root,node.right);
        
        
        if(node.left==null&&node.right==null){
            return;
        }
        else if(node.left!=null&&node.right==null){
            if(node.left.val==0){ //存在没有被覆盖的子节点，该节点设置为摄像头
                node.val=2;
                cameras++;
                return;
            }
            if(node.left.val==2) //子节点存在摄像头，该节点不需要设置为摄像头
                node.val=-1;
            if(node==root&&node.left.val!=2){  //根节点判断
                node.val=2;
                cameras++;
            }
            
        }
        else if(node.right!=null&&node.left==null){
            if(node.right.val==0){
                node.val=2;
                cameras++;
                return;
            }
            if(node.right.val==2)
                node.val=-1;
            if(node==root&&node.right.val!=2){
                node.val=2;
                cameras++;
            }
        }
        else{
            if((node.left.val==0||node.right.val==0)){
                node.val=2;
                cameras++;
                return;
            }
            if(node.left.val==2||node.right.val==2)
                node.val=-1;
            if(node==root&&node.left.val!=2&&node.right.val!=2){
                node.val=2;
                cameras++;
            }
        }
        return;
    }
}

991.坏了的计算器
难度：中等
在显示着数字的坏计算器上，我们可以执行以下两种操作：
双倍（Double）：将显示屏上的数字乘 2；
递减（Decrement）：将显示屏上的数字减 1 。
最初，计算器显示数字 X。
返回显示数字 Y 所需的最小操作数。

示例 1：

输入：X = 2, Y = 3
输出：2
解释：先进行双倍运算，然后再进行递减运算 {2 -> 4 -> 3}

示例 2：

输入：X = 5, Y = 8
输出：2
解释：先递减，再双倍 {5 -> 4 -> 8}

示例 3：

输入：X = 3, Y = 10
输出：3
解释：先双倍，然后递减，再双倍 {3 -> 6 -> 5 -> 10}

示例 4：

输入：X = 1024, Y = 1
输出：1023
解释：执行递减运算 1023 次

解：
执行用时 : 1 ms, 在Broken Calculator的Java提交中击败了98.98% 的用户
内存消耗 : 32 MB, 在Broken Calculator的Java提交中击败了97.58% 的用户
思路：转换成对Y进行+1与/2操作。
Code:

class Solution {
    public int brokenCalc(int X, int Y) {
        int res=0;
        while(X<Y){
            if(Y%2==0){
                Y/=2;
                res++;
            }
            else{   //Y为奇数时，必须先加一
                Y=(Y+1)/2;
                res+=2;
            }
        }
        //X>Y时，只能进行X递减操作
        res+=X-Y;
        return res;
    }
}