卡尔曼滤波算法---温度为例

假设房间温度大概在25℃左右，由于环境影响，空间温度小幅度波动。我们以分钟为单位，定时测量房间的温度。假设测量温度时，外界的天气是多云，阳光照射时有时无，同时房间不是100%封闭，可能有微小的与外界空气的交换，即引入噪声W(k)，其方差是Q，（补充：方差（Variance）：用来度量随机变量和其数学期望（即均值）之间的偏离程度。）方差的大小我们假设为Q=0.01（假如我们不考虑过程噪声的影响，认为环境是理想的，真是温度是恒定的，那么Q=0）。
考虑用如下状态空间模型描述的动态系统：

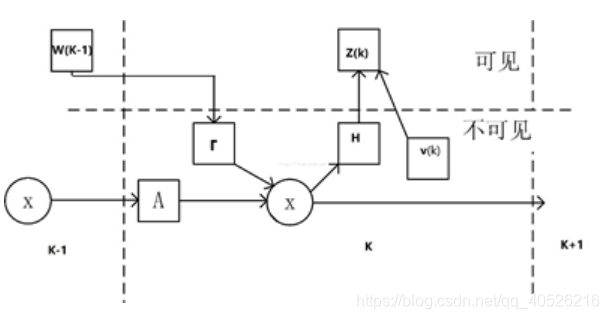
系统的状态方程为：用来表示真实值

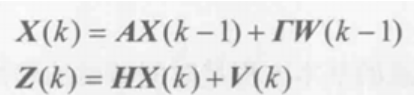
其中，K为离散时间，系统在时刻K的状态为X(k)，Φ为状态转移矩阵，W(k)为输入的白噪声，Q为输入白噪声的方差，┏为噪声驱动矩阵，；Z(k)对应状态的测量值，V(k)为观测噪声，H为观测矩阵，R是观测噪声的方差。

现在用温度计测量房子的温度，假设温度计的测量误差是：​​​​​，温度计厂说明书上写着温度计方差为0.25，也就是说温度计存在测量噪声V(k)，并且其方差为R=0.25。

我们总结一下我们假设或者获得的系数：A=1;┏=1；H=1；输入白噪声W(k)和观测V(k)的方差为Q=0.01和R=0.25。

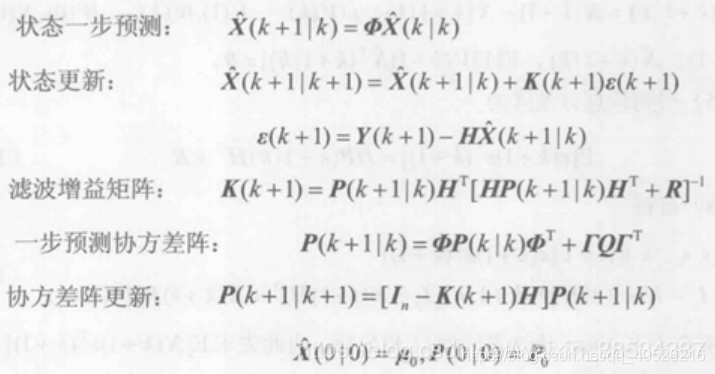
假如要估计第K时刻的实际温度，我们首先要根据第K-1时刻的温度来预测K时刻的温度。

1 假设第K-1时刻的温度值的测量值为24.1℃，房间里真实温度为24.0℃。实际测量值的偏差是0.1℃，即:Z(k-1)= 24.1℃；X(k-1)= 24.0℃；P(K