面了小米大模型岗,LLM量化技术成了送命题...
技术微佬 丁师兄大模型 2024年11月19日 20:44 湖北
随着 LLM 的发展和应用,显存降低和推理速度提升的需求越来越迫切,目前常用的方式就是对 LLM 参数量化,所谓的量化就是,对 LLM 中的参数做精度压缩(比如从每个参数需要 2/4byte 降低到 0.5/1byte)。
但是如果全量无差别压缩,势必会造成模型效果的降低,如果精准有效的压缩不重要参数,不(少)压缩重要参数是现在量化技术的重点。
整体来说:
GPTQ:是通过 OBS 算法一步步演化而来,主要是通过计算 hessian 矩阵(表示权重对损失的重要程度)来判断权重的重要性,压缩不重要的权重来达到量化的目的,同时算法也增加了批处理和 Cholesky 矩阵分解来提升计算速度和精度。
AWQ:是根据根据激活值大小来判断权重的重要性,选择0.1%~1%的重要权重,对其余权重做量化。
01
GPTQ
GPTQ 来自于 OBQ 的改进,OBQ 来自于 OBS,OBS 来自于 OBD 算法,OBD 算法是 1990 年 LeCun 提出的一种剪枝算法,所以下面简单介绍一下这个几个算法,以及这几个算法之间的区别和改进点。
(1)OBD 算法(Optimal Brain Damage)
OBD 算法是利用二阶信息对网络进行重要性评估,剪枝掉对结果影响最小的参数,具体实现步骤如下:
重要性评估:
OBD 首先通过评估各个权重的“重要性”来决定哪些权重可以被剪掉。重要性的评估通常基于 Hessian 矩阵,这个矩阵表示了损失函数在参数空间中的二阶导数。
具体来说,OBD 通过计算每个权重对损失函数的影响,评估其对模型性能的贡献。
二阶导数的信息:

剪枝策略:
OBD 根据各个权重的 Hessian 的值来决定是否剪枝。权重的“重要性”可以用以下公式估算:

剪去不重要的权重:
设定一个阈值,根据权重的重要性得分进行排序,剪去得分最低的若干个权重。此时,通过重新训练微调剩余权重,可以恢复模型的性能。
再训练:
剪除掉不重要的权重后,通常需要对模型进行再训练,以便让剩余的权重重新适应数据。这一过程也是非常重要,能够帮助模型保持或恢复原来的性能。
迭代优化:
OBD 可以进行多轮剪枝和再训练,逐步压缩模型,直到达到满意的性能与大小之间的平衡。
总结
OBD 算法通过评估权重的重要性,基于 Hessian 矩阵的信息实现了高效的剪枝。
这种方法为深度学习模型的压缩和加速提供了有效的解决方案。同时,由于它主要依赖于第二阶导数,因此在某些情况下,计算成本可能相对较高,需要权衡使用。
(2)OBS算法(Optimal Brain Surgeon)
OBS 算法也是根据 hessian 矩阵来做剪枝的,但是与 OBD 的不同是:
基本原理:
OBD 算法是关注的 hessian 矩阵的对角线元素,即单个权重的重要程度,剪枝也是只剪部分权重;
OBS 算法关注的是整个 hessian 矩阵,会剪枝整个神经元(即矩阵的行或列);
计算复杂度:
由于 OBD 算法仅依赖于 Hessian 矩阵的对角元素,因此它的计算成本相对较低。这使得 OBD 在较大的神经网络中更为实用。
OBS 算法需要处理完整的 Hessian 矩阵,这在大型神经网络中可能变得非常耗时和计算密集,因为它涉及矩阵求逆等操作。
精度与效果:
OBS 算法理论上能更精确地识别出哪些权重可以被剪枝,因为它考虑了权重之间的相互作用,而不仅仅是单个权重的影响。这可能导致更高的剪枝效率和更好的模型性能保留。
相比之下,OBD 算法可能在某些情况下过于简化,忽略了权重间的相互依赖性,但这并不意味着它总是次优的,特别是在计算资源有限的情况下。
应用范围:
OBD 算法因其较低的计算需求,在实际应用中更为广泛,尤其是在处理大规模数据集和复杂模型时。
OBS 算法由于其高计算成本,可能更适合于小到中等规模的网络或特定的研究场景,其中精度优化是首要考虑因素。

(3)OBQ 算法(Optimal Brain Quantization)
OBQ 算法是将 OBS 算法把它推广到量化中,其实很好理解,我们常用的量化则是把数值近似到一个接近的值, 而剪枝实际上可以看做把数值直接近似成 0 (某种意义上或许可以称作 1bit 或 0bit 量化),可以理解为一种特殊的量化。
OBQ 的公式:
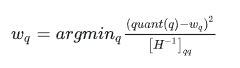
其中 quant(q) 是把 q 近似到四舍五入位数上。可以看到假如 quant(q) 永远返回零其实就是原版的 OBS。
(4)GPTQ
OBQ 算法的问题在于量化速度太慢,他的复杂度大约是参数矩阵维度的 4 次方,为了解决这个问题 GPTQ 做了如下改进:
取消贪心算法:原先的算法是使用贪心算法,逐个找影响最小的 q 来剪枝/量化,经过观察发现,其实随机的顺序效果也一样好(甚至在大模型上更好)。原算法对 W 进行优化时,逐行计算,每一行挑选 q 的顺序都是不一样的。
批处理:原先的算法中对权重一个个进行单独更新,作者发现瓶颈实际在于 GPU 的内存带宽,而且同一个特征矩阵 W 不同列间的权重更新是不会互相影响的。
因此作者提出了批处理的方法,一次处理多个(如 128 列)列,大幅提升了计算速度。

总结:GPTQ 通过 hessian 矩阵动态调整各个权重的精度,为了提升计算速度取消了贪心算法,增加了批处理和 Cholesky 分解来提升计算速度和精度。
02
AWQ算法
AWQ(Activation-aware Weight Quantization)量化是一种基于激活值分布挑选重要权重进行量化的方法,不依赖于任何反向传播或重建,因此可以很好地保持 LLM 在不同领域和模式上的泛化能力,而不会过拟合到校准集,属训练后量化(Post-Training Quantization, PTQ)大类。
上面加黑那句话需要解释两个点:

基于激活值分布挑选重要权重
作者对比了随机挑选、基于权重大小、基于激活值分布三种方案的效果,发现基于激活值分布挑选显著权重是最为合理的方式。
在做基于激活值分布时,作者为了避免方法在实现上过于复杂,在挑选显著权重时,并非在“元素”级别进行挑选,而是在“通道(channel)”级别进行挑选,即权重矩阵的一行作为一个单位。
在计算时,首先将激活值对每一列求绝对值的平均值,然后把平均值较大的一列对应的通道视作显著通道,保留 FP16 精度。
对其他通道进行低比特量化,如下图:
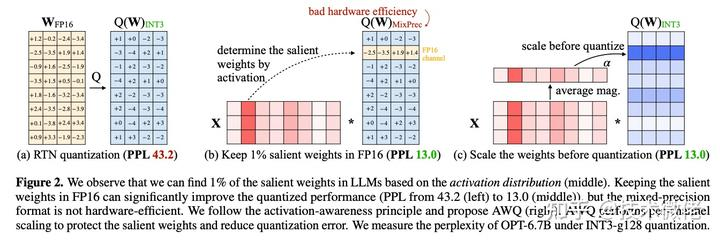
但另一个问题随之而来,如果权重矩阵中有的元素用 FP16 格式存储,有的用 INT4 格式存储,不仅存储时很麻烦,计算时取数也很麻烦,kernel 函数写起来会很抽象。于是,作者想了一个变通的方法——Scaling。
量化时对显著权重进行放大可以降低量化误差

虽然公式 1 和公式 2 在计算过程上是“等价”的,但是带来的精度损失是不一样的。
两种计算方法的误差可以写作公式 3:


因此,作者改变了思路:为了更加 hardware-friendly,我们对所有权重均进行低比特量化,但是,在量化时,对于显著权重乘以较大的 s,相当于降低其量化误差。
同时,对于非显著权重,乘以较小的 s,相当于给予更少的关注。这便是上一节提到的缩放(Scaling)方法。
(1)算法:自动计算缩放(scaling)系数
按照上文的分析,我们需要找到权重矩阵每个通道的缩放系数 s,使得量化误差最小,即最小化公式 4:

这里有个细节作者没有提,通过阅读源码发现,为了防止 s 过大或者过小,作者还进行了一步数据标准化:
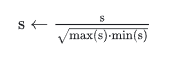

(图:llm-awq/awq/quantize/auto_scale.py第129-130行)

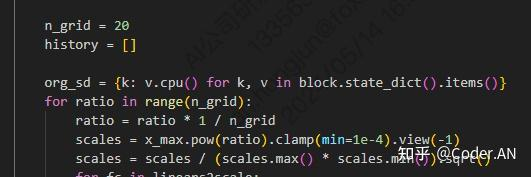
(图:llm-awq/awq/quantize/auto_scale.py第123-130行, for循环就是fast grid search算法)
将所有权重矩阵的 s 保存下来,供推理阶段反量化使用。
(2)算法超参数
如下图:

来源:https://zhuanlan.zhihu.com/p/720888766
END























 856
856

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








