机器学习入门

如需运行本文的代码请安装scikit-learn与matplotlib等必备的python包。

1. 机器学习概念

1.1 机器学习的基本定义

机器学习是人工智能的一个分支，它使计算机能够在不进行显式编程的情况下从数据中学习。简而言之，机器学习的目标是从数据中自动改进算法的行为。

1.2 用数学公式描述机器学习过程

f(x) = y 可以看作是一个模型或函数，这个函数将输入数据 x 映射到输出 y。在机器学习中，我们的目标是找到这样的一个函数 f，使得对于新的输入数据 x’，函数 f 能够给出准确的预测 y’。

1.2.1 目标函数 f(x)

• f(x)：这是我们要学习的函数，它将输入数据映射到输出结果。

1.2.2 损失函数（Loss Function）

• g(y0, f(x)) = yg：在这个表达式中，y0 可以被认为是真实的结果或者期望的输出，而 f(x) 是模型产生的预测结果。损失函数 g 是用来衡量模型预测结果与实际结果之间的差距。损失函数的值 yg 表示模型的误差大小。

1.2.3 参数优化

• 我们的目标是通过优化过程调整 f 中的参数，使得 g(y0, f(x)) 的值尽可能小。这通常通过迭代过程完成，比如使用梯度下降法等优化算法来最小化损失函数。

1.3 机器学习中的参数

在 f(x) = 2x 的例子中，2 是模型的参数。参数是函数中除了输入变量（自变量）以外的部分，它们决定了函数的行为。在更复杂的模型中，可能会有多个参数，例如在多项式回归中，f(x) = w_0 + w_1 * x + w_2 * x^2 + ... + w_n * x^n，其中 w_0, w_1, …, w_n 都是参数。

1.4 不同算法的参数优化

不同的机器学习算法有不同的方式来优化这些参数。例如：

• 线性回归：通过最小化预测值与真实值之间的平方差来优化参数。
• 逻辑回归：通过最大似然估计（MLE）或最小化交叉熵损失来优化参数。
• 神经网络：使用反向传播算法（Backpropagation）来调整权重（参数），以最小化损失函数。

1.5 参数优化方法

优化参数的方法包括但不限于：

• 梯度下降：通过计算损失函数关于每个参数的梯度，然后沿负梯度方向更新参数。
• 随机梯度下降（SGD）：每次只使用一个样本更新参数，可以更快地收敛，但路径会比较曲折。
• 批量梯度下降：使用所有训练样本计算梯度，然后更新参数。
• 动量方法：引入动量项来加速收敛。
• Adam优化器：结合了动量和自适应学习率的优点。

1.6 总结

为了简化理解，我们可以将机器学习的过程总结为以下步骤：

1. 定义模型 (f(x)): 选择一个能够描述输入与输出之间关系的函数形式。
2. 定义损失函数 (g(y0, f(x))): 设定一个度量标准来评估模型预测的准确性。
3. 优化参数: 使用优化算法调整模型参数，使得损失函数最小化。
4. 验证和测试: 在未见过的数据上验证模型性能，确保其具有良好的泛化能力。

机器学习算法能够在给定的数据集上“学习”，即通过调整模型参数来逼近真实的映射关系 f。这种方法允许模型随着更多数据的输入而不断改进其性能。

2. 决策树

决策树类似于 if-else 结构的编程逻辑，通过一系列的条件判断来做出最终的决策。以下是一个简化版的讲解方式，结合具体的例子来帮助学生更好地理解：

2.1 简化讲解框架

1. 引入决策树的概念：

   • 决策树是一种基于树结构的模型，用于分类或回归任务。
   • 决策树的工作原理类似于一系列嵌套的 if-else 条件语句。

2. 构建决策树的过程：

   • 从根节点开始构建。
   • 选择最佳属性作为分裂节点，目的是使子节点更加纯净（即子节点中的样本尽可能属于同一类别）。
   • 递归地应用此过程，直到达到停止条件。

3. 选择根节点：

   • 使用信息增益、增益率或基尼指数等度量来评估属性的重要性。
   • 选择信息增益最大（或基尼指数最小）的属性作为根节点。
   • 通俗解释：哪个节点对当前的结果影响最大，那么就选为。

2.2 具体例子

假设我们有一个关于天气的数据集，用来预测是否适合打网球。数据集如下：

天气	温度	湿度	风速	是否打网球
晴	热	高	弱	是
晴	热	高	强	否
阴	热	高	弱	是
雨	温	高	弱	是
雨	冷	正常	弱	是
雨	冷	正常	强	否
阴	冷	高	弱	是
晴	温	高	弱	否
晴	冷	正常	强	否
雨	温	正常	弱	是
晴	温	正常	强	是
阴	温	高	强	是
阴	热	正常	弱	是
雨	温	高	强	否

计算信息增益：

好的，让我们详细探讨一下信息熵和信息增益的概念及其计算方法。

2.2 信息熵（Entropy）

信息熵是用来量化信息不确定性的度量。在决策树中，熵用来衡量一个数据集的纯度。熵越高，表示数据集中的信息越不确定；熵越低，表示数据集中的信息越纯净（即数据集中大部分样本属于同一类）。

2.2.1 计算公式

对于一个具有 $c$个类别的数据集$D$，其熵$Entropy(D)$ 可以定义为：

$$Entropy(D)=-\sum _{i=1}^c{p}_i{\log }_2(p_i)$$

其中 $p_i$ 是第 $i$ 类样本占总样本的比例。如果某类$i$ 的样本数量为零，则 $p_i{\log }_2(p_i)$ 的值为零。

2.2.2 例子

假设一个数据集 $D$包含 14 个样本，其中 9 个正类（标记为 “是”），5 个负类（标记为 “否”），则：

$$Entropy(D)=-\left(\frac{9}{14}{\log }_2(\frac{9}{14})+\frac{5}{14}{\log }_2(\frac{5}{14})\right)$$

计算得：

$$Entropy(D)\approx 0.940$$

2.3 条件熵（Conditional Entropy）

条件熵用来衡量在已知某一随机变量的情况下另一随机变量的不确定性。在决策树中，条件熵 $Entropy(D|A)$ 表示在属性 $A$ 已知的情况下数据集 $D$ 的熵。

2.3.1 计算公式

$$Entropy(D|A)=\sum _{v\in Values(A)}\frac{|D_v|}{|D|}Entropy(D_v)]$$

其中 $D_v$ 是数据集 $D$ 中属性$A$ 取值为 $v$ 的子集，$|D_v|$ 是子集 $D_v$ 的大小。

2.3.2 例子

如果我们用前面提到的天气数据集，并考虑属性 “天气”，则：

E n t r o p y ( D ∣ 天气 ) = ∑ v ∈ { 晴 , 阴 , 雨 } ∣ D v ∣ ∣ D ∣ E n t r o p y ( D v ) Entropy(D|天气) = \sum_{v \in \{\text{晴}, \text{阴}, \text{雨}\}} \frac{|D_v|}{|D|} Entropy(D_v) Entropy(D∣天气)=v∈{晴,阴,雨}∑​∣D∣∣Dv​∣​Entropy(Dv​)

假设$$|D_{晴}|=5$$，$$|D_{阴}|=4$$，$$|D_{雨}|=5$$，则：

$$Entropy(D|天气)=\frac{5}{14}Entropy(D_{晴})+\frac{4}{14}Entropy(D_{阴})+\frac{5}{14}Entropy(D_{雨})$$

2.3 信息增益（Information Gain）

信息增益是通过某个属性 ( A ) 分割数据集后，信息熵减少的程度。信息增益越大，表示该属性对数据集的分类能力越强。

2.3.1 计算公式

$$IG(A)=Entropy(D)-Entropy(D|A)$$

2.3.2 例子

如果我们继续使用之前的天气数据集：

$$IG(天气)=Entropy(D)-Entropy(D|天气)$$

假设我们已经计算出 $$Entropy(D)=0.940$$，$$Entropy(D|天气)=0.694$$，则：

$$IG(天气)=0.940-0.694=0.246$$

2.4 总结

• 信息熵 用来度量数据集的不确定性。
• 条件熵 用来度量在给定另一个属性的情况下数据集的不确定性。
• 信息增益 是通过某个属性分割数据集后信息熵的减少量，用于选择最佳的分割属性。

通过计算信息增益，我们可以选择出对数据集分类最有贡献的属性，并以此构建决策树的分支。希望这个详细的解释能够帮助你更好地理解信息熵和信息增益的概念及计算方法。

假设我们计算得到的信息增益如下：

• IG(天气) ≈ 0.246
• IG(温度) ≈ 0.029
• IG(湿度) ≈ 0.152
• IG(风速) ≈ 0.048

2.5 构建决策树

• 选择信息增益最大的属性作为根节点，这里是“天气”。
• 接下来对每个天气条件下的子集重复上述过程，选择子集内信息增益最大的属性。

2.6 结果决策树

如果 天气 = 晴
  如果 湿度 = 高 -> 不打网球
  如果 湿度 = 正常 -> 打网球
如果 天气 = 阴 -> 打网球
如果 天气 = 雨
  如果 风速 = 弱 -> 打网球
  如果 风速 = 强 -> 不打网球

好的，理解你的需求后，我会尽量简化逻辑回归和线性回归的概念，并通过具体的例子来说明它们各自的应用场景。

3. 逻辑/线性回归

3.1. 线性回归（Linear Regression）

3.1.1 应用场景

线性回归用于预测一个连续型的目标变量，例如温度、价格、湿度等。

3.1.2 原理

线性回归假设输入特征与目标变量之间存在线性关系。通过拟合一条直线（或超平面），使得这条直线与实际观测值之间的误差最小。

3.1.3 例子

假设我们有一组关于房价的数据，其中包括房屋面积和房价。

房屋面积 (平方米)	价格 (万元)
80	200
100	250
120	300
150	350
…	…

3.1.4 模型

我们假设价格 $y$ 与房屋面积 $x$ 之间存在线性关系：

$$y={\beta }_0+{\beta }_{1}x$$

其中：

• ${\beta }_0$ 是截距。
• ${\beta }_1$ 是斜率。

3.1.5 目标

我们的目标是找到${\beta }_0$和 ${\beta }_1$，使得预测的价格与实际价格之间的差距最小。

3.1.6 解决方法

通常使用最小二乘法来找到最优的${\beta }_0$ 和${\beta }_1$。

3.2. 逻辑回归（Logistic Regression）

3.2.1 应用场景

逻辑回归用于预测一个离散型的目标变量，例如是否患病（是/否）、是否点击广告（是/否）等。

3.2.2 原理

逻辑回归通过 Sigmoid 函数（Logistic 函数）将线性组合的输出转换为概率值，从而预测目标变量属于某一类的概率。

3.2.3 例子

假设我们要预测一个患者是否患有糖尿病，特征包括患者的年龄、体重等。

年龄 (岁)	体重 (公斤)	是否患病 (是/否)
30	70	否
45	85	是
50	90	是
25	65	否
…	…	…

3.2.4 模型

我们假设患病的概率 $P(y=1|x)$ 与特征 $x$ 之间存在关系：

$$P(y=1|x)=\frac{1}{1+e^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_n{x}_n)}}$$

其中：

• $P(y=1|x)$是患病的概率。
• ${\beta }_0,{\beta }_1,{\beta }_2,\dots ,{\beta }_n$ 是模型参数。

3.2.5 目标

我们的目标是找到${\beta }_0,{\beta }_1,{\beta }_2,\dots ,{\beta }_n$，使得预测的概率与实际患病状态之间的差距最小。

3.2.5 解决方法

通常使用梯度下降法来找到最优的参数。

3.3 总结

• 线性回归 用于预测连续型的目标变量，例如房价、温度等。
• 逻辑回归 用于预测离散型的目标变量，例如是否患病、是否点击广告等。

4. KNN与K-means

4.1 KNN（K-最近邻算法）

简单解释：某物体和现有物体的各项参数毕竟相近，那么其类别也就更可能是现有物体的类别。例如：苹果通常是红色的，球形的，电脑显示屏通常是黑色的、方块的。现在有一个物品A是方形的黑色的，另一个物品B是绿色的，球形的。请问，物品B更可能是苹果还是饼干？

4.1.1 应用场景

KNN 主要用于分类任务，也可以用于回归任务。它可以用来预测新数据点所属的类别。

4.1.2 原理

KNN 的核心思想是通过测量不同特征值之间的距离，找出与新数据点最相似的 k 个邻居，然后根据这些邻居的多数类别来预测新数据点的类别。

4.1.3 算法步骤

1. 计算距离：计算新数据点与训练集中的每个数据点之间的距离。
2. 选择邻居：选择距离最近的 k 个邻居。
3. 投票分类：根据这 k 个邻居的类别进行投票，新数据点的类别由多数类别决定。

4.1.4 例子

假设我们有一个数据集，包含身高和体重两个特征，用于预测性别（男性或女性）。

身高 (cm)	体重 (kg)	性别
170	70	男
165	60	女
180	80	男
155	50	女
…	…	…

假设我们要预测一个新数据点（身高 160 cm，体重 55 kg）的性别。

4.1.5 实际操作

1. 计算距离：计算新数据点与已有数据点之间的欧氏距离。
2. 选择邻居：假设 k=3，选出距离最近的三个邻居。
3. 投票分类：假设选出的三个邻居中有两个女性和一个男性，则预测新数据点的性别为女性。

4.2 K-Means（K-均值算法）

4.2.1 应用场景

K-Means 是一种无监督学习算法，主要用于聚类任务。它可以将数据分成 k 个簇（cluster），每个簇内的数据点彼此相似。

4.2.2 原理

K-Means 试图通过迭代的方式，找到数据集中 k 个中心点（质心），使得每个数据点到最近的质心的距离之和最小。

4.2.3 算法步骤

1. 初始化质心：随机选择 k 个数据点作为初始质心。
2. 分配数据点：将每个数据点分配给最近的质心所在的簇。
3. 更新质心：重新计算每个簇的质心位置。
4. 重复步骤2和3：直到质心不再改变或达到最大迭代次数。

4.2.4 例子

假设我们有一个数据集，包含一些点的位置坐标（X, Y），我们想要将这些点分成 k=3 个簇。

X坐标	Y坐标
2	10
2	5
8	4
5	8
7	5
6	4
1	2
4	9
…	…

4.2.5 实际操作

1. 初始化质心：随机选择 3 个点作为初始质心。
2. 分配数据点：计算每个点到每个质心的距离，并将其分配给最近的质心。
3. 更新质心：重新计算每个簇的质心位置。
4. 重复步骤2和3：直到质心不再改变。

4.3 代码实现

4.3.1 KNN 的 Python 代码实现

4.3.1.1 数据集

我们将使用随机生成的数据集来演示 KNN。

4.3.1.2 代码实现

import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from matplotlib import pyplot as plt

# 随机生成数据集
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2,
                           random_state=1, n_clusters_per_class=1)

# 标准化数据
scaler = StandardScaler()
X = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建 KNN 分类器
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

# 预测测试集
y_pred = knn.predict(X_test)

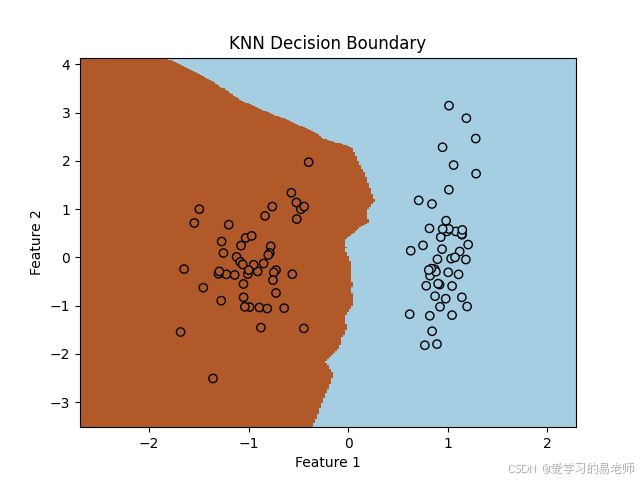
# 绘制决策边界
h = .02  # step size in the mesh
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k', cmap=plt.cm.Paired)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('KNN Decision Boundary')
plt.show()

print("Accuracy:", np.mean(y_pred == y_test))

4.3.2 K-Means 的 Python 代码实现

4.3.2.1 数据集

我们同样使用随机生成的数据集来演示 K-Means。

4.3.2.2 代码实现

import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from matplotlib import pyplot as plt

# 随机生成数据集
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.6, random_state=0)

# 创建 K-Means 模型
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, alpha=0.5)
plt.title('K-Means Clustering')
plt.show()

4.3.3 使用公有数据集

4.3.3.1 数据集

我们将使用著名的 Iris 数据集来演示 KNN 和 K-Means。

4.3.3.2 数据集下载

你可以从 UCI 机器学习库下载 Iris 数据集：

• Iris 数据集

4.3.3.3 KNN 使用 Iris 数据集

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from matplotlib import pyplot as plt

# 加载 Iris 数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 标准化数据
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 创建 KNN 分类器
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

# 预测测试集
y_pred = knn.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

4.3.3.4 K-Means 使用 Iris 数据集

import numpy as np
from sklearn import datasets
from sklearn.cluster import KMeans
from matplotlib import pyplot as plt

# 加载 Iris 数据集
iris = datasets.load_iris()
X = iris.data

# 创建 K-Means 模型
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, alpha=0.5)
plt.title('K-Means Clustering on Iris Data')
plt.show()

4.4 总结

• KNN 是一种监督学习算法，用于分类或回归任务。它通过找到最接近的新数据点的 k 个邻居来预测新数据点的类别。
• K-Means 是一种无监督学习算法，用于聚类任务。它通过迭代地更新质心的位置来将数据分成 k 个簇。

当然可以！支持向量机（Support Vector Machine, SVM）是一种非常强大的机器学习算法，主要用于分类和回归任务。下面我将用简单的语言来讲解SVM的基本概念和工作原理。

5 支持向量机（SVM）简介

本文不涉及支持向量机的具体数学讲解，支持向量机是一个最优化问题，其涉及的诸多数学概念请前往：【超详细】支持向量机（SVM）数学推导

5.1 应用场景

支持向量机主要用于分类任务，也可以用于回归任务。例如，预测邮件是否为垃圾邮件、图像识别、手写数字识别等。

5.2 原理

支持向量机的核心思想是找到一个最优的决策边界（称为超平面），使得不同类别的数据点在这个边界两侧尽可能分开，并且边界两侧的数据点离边界尽可能远。

5.3 简单的例子

5.3.1 二维数据

假设我们有一组二维数据，每个数据点有两个特征（例如，身高和体重），并且有两个类别（例如，男性和女性）。

身高 (cm)	体重 (kg)	类别
170	70	男
165	60	女
180	80	男
155	50	女
…	…	…

5.3.2 目标

我们的目标是找到一个决策边界，使得男性和女性的数据点在这个边界两侧尽可能分开。

5.4 如何找到决策边界？

5.4.1 最大间隔

支持向量机试图找到一个决策边界，使得离边界最近的数据点（称为支持向量）到边界的距离最大化。这个最大化的距离称为间隔（margin）。
解释：决策边界可以有无限多个，每个决策边界必然有离其最近（直线距离最近）的点。这个点距离边界的距离为 ”离边界最近的数据点（称为支持向量）到边界的距离“
现在我们渴望找到一个边界，其在所有决策边界中这个点距离边界的距离最大。

5.4.2 超平面

在二维空间中，决策边界是一条直线；在三维空间中，决策边界是一个平面；在更高维度的空间中，决策边界被称为超平面。

5.4.3 支持向量

支持向量是指离决策边界最近的数据点。这些点直接影响决策边界的形状和位置。

5.5 简单的实现步骤

1. 画出数据点：将数据点在二维平面上标出。
2. 找到决策边界：尝试画出一条直线，使得两个类别的数据点尽可能分开。
3. 最大化间隔：调整这条直线，使得离直线最近的数据点到直线的距离尽可能大。
4. 分类新数据点：对于新的数据点，根据它在决策边界的一侧还是另一侧来判断其类别。

5.6 例子

假设我们有一组数据点，其中有些点标记为红色（类别 A），有些点标记为蓝色（类别 B）。

5.6.1 数据点可视化

红色点 (类别 A)：
(1, 2), (2, 3), (3, 4)

蓝色点 (类别 B)：
(6, 7), (7, 8), (8, 9)

5.6.2 找到决策边界

我们可以尝试画出一条直线，使得红色点和蓝色点尽可能分开。例如，直线 $y=x+3$ 可以很好地将这两类点分开。

5.6.3 最大化间隔

调整直线的位置，使其离最近的数据点（支持向量）的距离尽可能大。例如，直线 $y=x+3$ 可能不是最佳的，我们可以通过调整找到一条更优的直线。

5.6.4 分类新数据点

假设有一个新的数据点 $(4,5)$，它位于直线 $y=x+3$的一侧，因此我们可以判断它是类别 A。

5.7 Python 实现

下面是一个简单的 Python 代码实现，使用 scikit-learn 库来展示 SVM 的基本使用方法：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

# 生成数据集
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=1.5)

# 创建 SVM 分类器
clf = svm.SVC(kernel='linear', C=1.0)

# 训练模型
clf.fit(X, y)

# 绘制决策边界和支持向量
def plot_svm_boundary(clf, ax=None):
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    # 创建网格来评价模型
    xx = np.linspace(xlim[0], xlim[1], 30)
    yy = np.linspace(ylim[0], ylim[1], 30)
    YY, XX = np.meshgrid(yy, xx)
    xy = np.vstack([XX.ravel(), YY.ravel()]).T
    Z = clf.decision_function(xy).reshape(XX.shape)
    
    # 绘制决策边界和支持向量
    ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
               s=300, linewidth=1, facecolors='none')
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svm_boundary(clf)
plt.show()

5.9 其它

核函数（Kernel Function）

核函数是支持向量机（SVM）中的一个重要概念，它用于处理非线性可分的数据集。当我们面对的是非线性问题时，直接在原空间中寻找一个线性决策边界可能无法很好地分离数据。这时就需要使用核函数将数据映射到一个更高维的空间，在这个新空间中，数据可能变得线性可分。

核函数的主要作用是将原始数据从低维空间映射到一个高维空间，使得原本在低维空间中不可分的数据在高维空间中变得可分。具体来说，核函数可以将非线性问题转化为线性问题，从而使 SVM 能够处理更复杂的分类任务。

5.8 总结

支持向量机是一种寻找最优决策边界的机器学习算法。通过最大化间隔来确保决策边界的鲁棒性。支持向量是离决策边界最近的数据点，它们决定了决策边界的位置。

实践作业

1.基于SVM的手写数字识别

#利用AI 实现一个分类任务：尝试运行一下代码：
import paddle
from paddle.vision import transforms
from paddle.vision.datasets import MNIST
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
import numpy as np

# 使用PaddlePaddle加载MNIST数据集
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.5], std=[0.5])  # 归一化到 [-1, 1]
])
train_dataset = MNIST(mode='train', transform=transform)
test_dataset = MNIST(mode='test', transform=transform)

# 将数据转换成numpy格式
train_data = [(sample[0].numpy().astype("float32").flatten(), sample[1]) for sample in train_dataset]
test_data = [(sample[0].numpy().astype("float32").flatten(), sample[1]) for sample in test_dataset]

# 提取特征和标签
train_features, train_labels = zip(*train_data)
test_features, test_labels = zip(*test_data)
# 检查训练数据中是否存在无限大或NaN
if np.any(np.isinf(train_features)) or np.any(np.isnan(train_features)):
    print("训练数据中存在无限大或NaN值")
# 检查测试数据
if np.any(np.isinf(test_features)) or np.any(np.isnan(test_features)):
    print("测试数据中存在无限大或NaN值")

# 转换为numpy数组并确保标签是一维的
train_features = np.array(train_features)
test_features = np.array(test_features)
train_labels = np.array(train_labels).ravel()  # 使用ravel()确保是一维数组
test_labels = np.array(test_labels).ravel()    # 同上
# 数据标准化
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
test_features = scaler.transform(test_features)

# 划分训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(train_features, train_labels, test_size=0.1, random_state=42)

# 创建SVM分类器
svm_classifier = SVC(decision_function_shape='ovo', kernel='rbf')

# 训练模型
svm_classifier.fit(X_train, y_train)

# 在验证集上评估模型
y_pred = svm_classifier.predict(X_val)

# 输出分类报告
print(classification_report(y_val, y_pred))

2.基于SVM的花分类

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

x = [[5.1, 3.5, 1.4, 0.2], [4.9, 3.0, 1.4, 0.2], [4.7, 3.2, 1.3, 0.2], [4.6, 3.1, 1.5, 0.2], [5.0, 3.6, 1.4, 0.2],
     [5.4, 3.9, 1.7, 0.4], [4.6, 3.4, 1.4, 0.3], [5.0, 3.4, 1.5, 0.2], [4.4, 2.9, 1.4, 0.2], [4.9, 3.1, 1.5, 0.1],
     [5.4, 3.7, 1.5, 0.2], [4.8, 3.4, 1.6, 0.2], [4.8, 3.0, 1.4, 0.1], [4.3, 3.0, 1.1, 0.1], [5.8, 4.0, 1.2, 0.2],
     [5.7, 4.4, 1.5, 0.4], [5.4, 3.9, 1.3, 0.4], [5.1, 3.5, 1.4, 0.3], [5.7, 3.8, 1.7, 0.3], [5.1, 3.8, 1.5, 0.3],
     [5.4, 3.4, 1.7, 0.2], [5.1, 3.7, 1.5, 0.4], [4.6, 3.6, 1.0, 0.2], [5.1, 3.3, 1.7, 0.5], [4.8, 3.4, 1.9, 0.2],
     [5.0, 3.0, 1.6, 0.2], [5.0, 3.4, 1.6, 0.4], [5.2, 3.5, 1.5, 0.2], [5.2, 3.4, 1.4, 0.2], [4.7, 3.2, 1.6, 0.2],
     [4.8, 3.1, 1.6, 0.2], [5.4, 3.4, 1.5, 0.4], [5.2, 4.1, 1.5, 0.1], [5.5, 4.2, 1.4, 0.2], [4.9, 3.1, 1.5, 0.2],
     [5.0, 3.2, 1.2, 0.2], [5.5, 3.5, 1.3, 0.2], [4.9, 3.6, 1.4, 0.1], [4.4, 3.0, 1.3, 0.2], [5.1, 3.4, 1.5, 0.2],
     [5.0, 3.5, 1.3, 0.3], [4.5, 2.3, 1.3, 0.3], [4.4, 3.2, 1.3, 0.2], [5.0, 3.5, 1.6, 0.6], [5.1, 3.8, 1.9, 0.4],
     [4.8, 3.0, 1.4, 0.3], [5.1, 3.8, 1.6, 0.2], [4.6, 3.2, 1.4, 0.2], [5.3, 3.7, 1.5, 0.2], [5.0, 3.3, 1.4, 0.2],
     [7.0, 3.2, 4.7, 1.4], [6.4, 3.2, 4.5, 1.5], [6.9, 3.1, 4.9, 1.5], [5.5, 2.3, 4.0, 1.3], [6.5, 2.8, 4.6, 1.5],
     [5.7, 2.8, 4.5, 1.3], [6.3, 3.3, 4.7, 1.6], [4.9, 2.4, 3.3, 1.0], [6.6, 2.9, 4.6, 1.3], [5.2, 2.7, 3.9, 1.4],
     [5.0, 2.0, 3.5, 1.0], [5.9, 3.0, 4.2, 1.5], [6.0, 2.2, 4.0, 1.0], [6.1, 2.9, 4.7, 1.4], [5.6, 2.9, 3.6, 1.3],
     [6.7, 3.1, 4.4, 1.4], [5.6, 3.0, 4.5, 1.5], [5.8, 2.7, 4.1, 1.0], [6.2, 2.2, 4.5, 1.5], [5.6, 2.5, 3.9, 1.1],
     [5.9, 3.2, 4.8, 1.8], [6.1, 2.8, 4.0, 1.3], [6.3, 2.5, 4.9, 1.5], [6.1, 2.8, 4.7, 1.2], [6.4, 2.9, 4.3, 1.3],
     [6.6, 3.0, 4.4, 1.4], [6.8, 2.8, 4.8, 1.4], [6.7, 3.0, 5.0, 1.7], [6.0, 2.9, 4.5, 1.5], [5.7, 2.6, 3.5, 1.0],
     [5.5, 2.4, 3.8, 1.1], [5.5, 2.4, 3.7, 1.0], [5.8, 2.7, 3.9, 1.2], [6.0, 2.7, 5.1, 1.6], [5.4, 3.0, 4.5, 1.5],
     [6.0, 3.4, 4.5, 1.6], [6.7, 3.1, 4.7, 1.5], [6.3, 2.3, 4.4, 1.3], [5.6, 3.0, 4.1, 1.3], [5.5, 2.5, 4.0, 1.3],
     [5.5, 2.6, 4.4, 1.2], [6.1, 3.0, 4.6, 1.4], [5.8, 2.6, 4.0, 1.2], [5.0, 2.3, 3.3, 1.0], [5.6, 2.7, 4.2, 1.3],
     [5.7, 3.0, 4.2, 1.2], [5.7, 2.9, 4.2, 1.3], [6.2, 2.9, 4.3, 1.3], [5.1, 2.5, 3.0, 1.1], [5.7, 2.8, 4.1, 1.3]]

y = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
# 下面这两步可以不要 但是建议转为numpy数组
x = np.array(x)
y = np.array(y)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)

# 特征缩放（对于SVM来说很重要，因为SVM对特征尺度敏感）
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 创建SVM分类器并训练
clf = SVC(kernel='linear', C=1.0, random_state=42)  # 可以选择不同的核函数和正则化参数
clf.fit(X_train, y_train)

# 使用测试集进行预测
y_pred = clf.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy * 100:.2f}%")
# 预测
print(clf.predict([[-0.8, -0.8, -0.8, -0.8]]))

可以使用AI编程。