一、群智能计算简介
(一) 群智能(Swarm Intelligence, SI)的概念
无智能或简单智能的主体通过任何形式的聚集协同而表现出智能行为的特性。— by Bonabeau
生物群中的每个个体只有简单的信息处理能力和行为能力
- 鸟群:飞行,捕食,避碰....
- 昆虫:爬行,觅食,产生信息素....
群体中各个个体之间可以进行信息交互
- 鸟群:视觉、听觉、磁场....
- 昆虫:感知信息素....
群体的能力要远远超出个体能力的简单叠加
- 信息感知能力
- 分工协作能力
- 适应生存能力
Mark Millonas在1994年定义SI的五条基本原则
- Proximity Principle:群内个体具有能执行简单的时间或空间上的评估和计算的能力。
- Quality Principle:群内个体能对环境(包括群内其它个体)的关键性因素的变化做出响应。
- Principle of Diverse Response:群内不同个体对环境中的某一变化所表现出的响应行为具有多样性。
- Stability Principle:不是每次环境的变化都会导致整个群体的行为模式的改变。
- Adaptability Principle:环境所发生的变化中,若出现群体值得付出代价的改变机遇,群体必须能够改变其行为模式。
(二) 群智能算法与演化计算的异同
SI与EC的相同点
- 都研究个体与群体的关系
- 都存在个体之间的信息传递
- 都是为了解决实际问题,而非单纯的模拟自然现象
- 都属于随机搜索算法
SI与EC的不同点
- SI模拟的是个体之间的协同作用,而EC模拟的是适者生存的自然选择机制。
(三) 群智能算法:
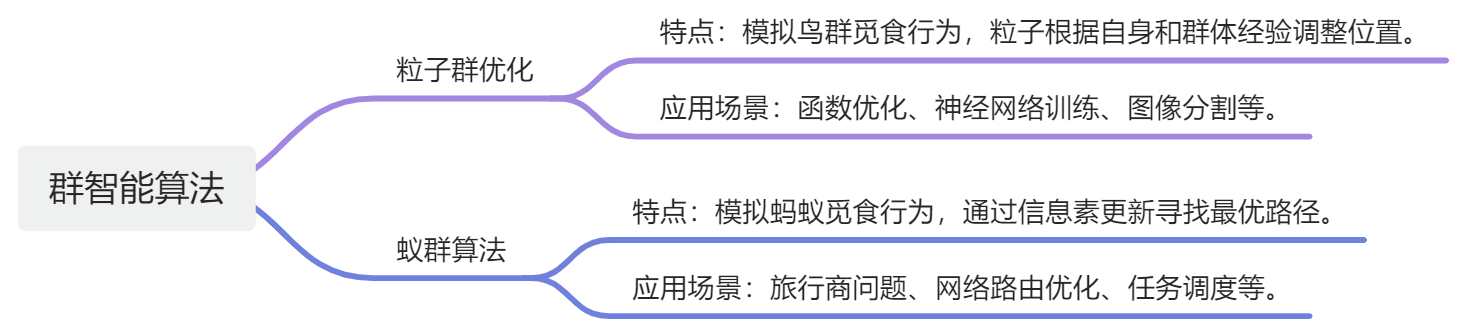
- 粒子群算法:模拟鸟群觅食行为
- 蚁群算法:模拟蚁群觅食行为
- 其他群体智能算法:
-
- 鱼群算法
- 蜂群算法
- ......
二、粒子群算法概述
(一) 粒子群算法的概念
粒子群优化算法(Particle Swarm Optimization,简称PSO)又称为粒子群算法、微粒算法,是通过模拟鸟类群体觅食行为而发展起来的一种基于群体协作的随机搜索算法,属于启发式全局优化算法。
粒子群算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
(二) 粒子群算法的发展
1. 第一阶段:萌芽阶段
1986年,人工生命、计算机图形学专家Craig Reynolds提出了简单的人工生命系统——boid模型(解释为bird like object),模拟了鸟类在飞行过程中分离、列队和聚集三种聚群飞行行为,并能感知到周围一定范围内其他boid的飞行信息。
boid根据该信息,结合当前自身的飞行状态,在三条简单行为规则的指导下,做出下一步的飞行决策。
➢避免碰撞:飞离最近的个体,以避免碰撞;
➢速度一致:和邻近的个体的平均速度保持一致;
➢向中心聚集:飞向群体的中心,向邻近个体的平均位置移动。
1990年,生物学家Frank Heppner建立了鸟类模型。一群鸟为找到合适的栖息地在空中飞行,当群体中的一只发现较为合适的栖息地时,它会毫不犹豫地飞向这个栖息地,同时将信息传给周围的鸟,使周围的鸟快速来到这里,最终把整个群体吸引到合适的栖息地。
2. 第二阶段:发展阶段
1995年,美国社会心理学家James Kennedy博士和电气工程师Russel Eberhart博士根据对鸟群捕食行为的研究,提出粒子群算法。分别在日本和澳大利亚召开的两个国际会议上发表了两篇文章,标志着粒子群算法的诞生。
Kennedy J,Eberhart R,Particle swarm optimization,Proceeding of the IEEE International Conference on Neural Networks,1995,1942~1948
Eberhart R,Kennedy J,A new optimizer using particle swarm theory,Proceeding of the 6th International Symposium on Micro-Machine and Human Science,1995,39~43
1998年,Yuhui Shi和Russell Eberhart在IEEE Congress on Evolution-ary Computation(69~73)上发表了题为A modified particle swarm optimizer的学术论文,首次对基本粒子群算法引入惯性权重修正了速度更新公式,修正后的公式已经得到广泛使用。
从1998年开始,进化计算领域的著名会议IEEE CEC(Congress on Evolutionary Computation,国际进化计算会议)开始设置PSO算法的专题讨论,与计算智能相关的重要国际会议PPSN(Parallel Problem Solving from Nature)和GECCO(Genetic and Evolutionary Computation Conference)都将PSO算法作为会议主题之一。
2001年,由J.Kennedy、 R.C.Eberhart、Yuhui Shi合著的第一本关于PSO的专著《Swarm Intelligence》在美国旧金山(San Francisco)Morgan Kaufmann Publishers出版。
2004年,IEEE Transactions on Evolutionary Computation出版了PSO算法专刊。
PSO算法作为一种新兴智能仿生算法,目前还没有完备的数学理论基础,但作为新兴优化算法已在诸多领域得到广泛应用。
(三) 重要学术期刊
IEEE Transactions on Evolutionary Computation
IEEE Transactions on Systems, Man and Cybernetics
Machine Learning
Evolutionary Computation
……
(四) 重要国际会议
IEEE Congress on Evolutionary Computation (CEC)
IEEE International Conference on Systems, Man, and Cybernetics (SMC)
ACM Genetic and Evolutionary Computation Conference (GECCO)
International Conference on Ant Colony Optimization and Swarm Intelligence (ANTS)
International Conference on Simulated Evolution And Learning (SEAL)
……
(五) 粒子群算法的分类
按照发展历程分类:一般分为传统粒子群算法和改进型粒子群算法。前者与1995年提出,后者则是对传统粒子群算法改进产生的粒子群算法。
按照粒子领域分类:一般分为全局最优粒子群算法和局部最优粒子群算法。
三、粒子群算法原理
(一) 生理学机理
设想这样一个场景:一群鸟在一个区域里随机搜索食物,已知:
- 在这块区域里只有一块食物
- 所有的鸟都不知道食物在哪里
- 但它们记得每次离食物有多远
那么找到食物的最优策略是什么?
就是朝着自己飞行过的最佳位置前进的同时,追寻目前离食物最近的鸟的位置。
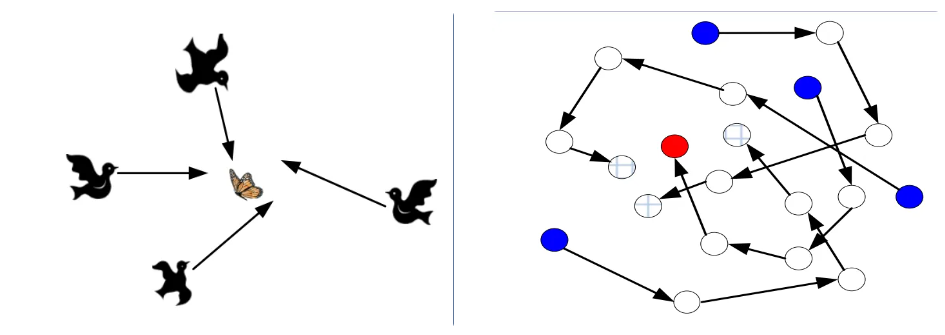
PSO正是从这种模型中得到启发。
PSO的基础:信息的社会共享。
粒子群算法中,每个优化问题的解都是搜索空间中的一只鸟,称之为“粒子”。所有的粒子都有一个由优化函数决定的适应度值(fitness value),每个粒子还有一个速度决定它们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中进行搜索。
粒子群算法首先初始化一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己。第一个是粒子本身所找到的最优解,称为个体极值pbest,另一个是整个种群目前找到的最优解,称为全局极值gbest。另外也可以不用整个种群而只用其中一部分相邻的粒子,则这些相邻粒子中的极值是局部极值。
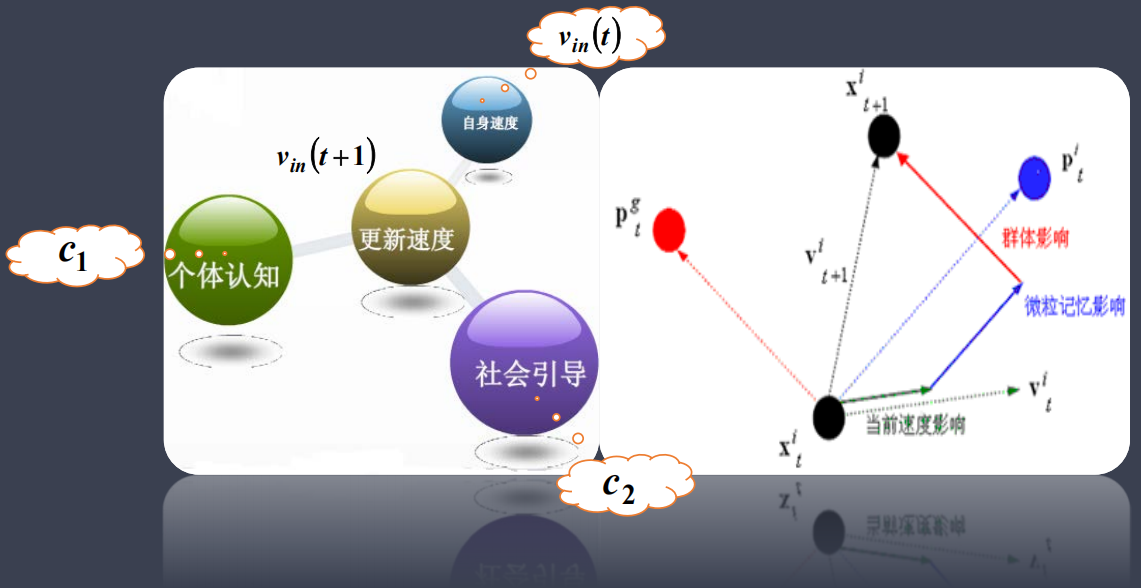
鸟群觅食与粒子群算法的类比关系:
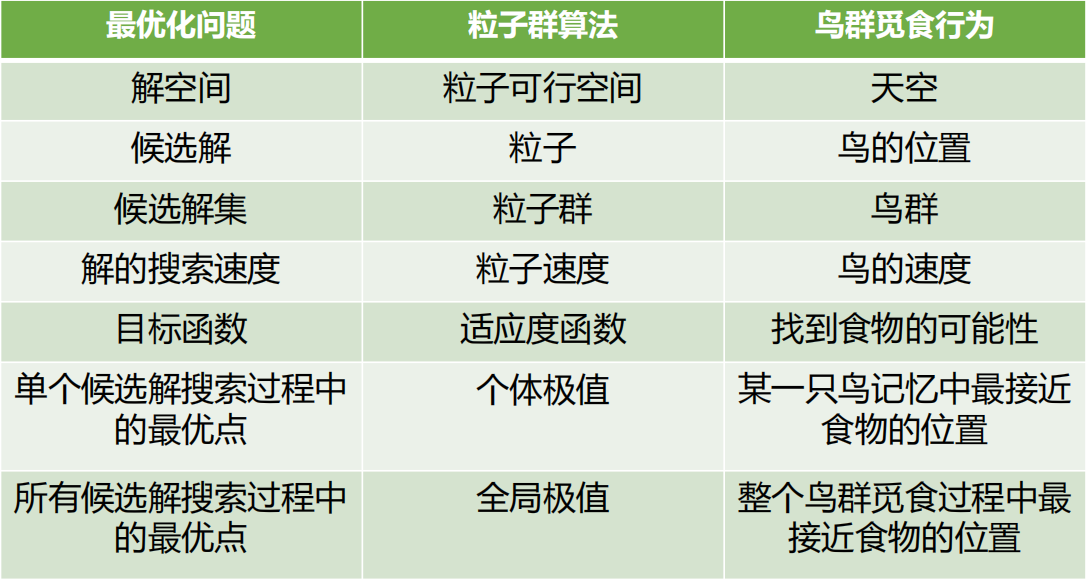
(二) 粒子群算法的一般流程
Step1:初始化一群微粒,包括随机位置和速度。
Step2:评价每个微粒的适应度值。
Step3:将每个微粒的适应度值与其经过的最好位置pbest进行比较,如果较好则将其作为当前的最好位置pbest。
Step4:将每个微粒的适应度值与种群的最好位置gbest进行比较,如果较好则将其作为种群的最好位置gbest。
Step5:根据速度和位置公式调整粒子的飞行速度和所处位置。
Step6:判断是否达到结束条件,若未达到转到Step2。
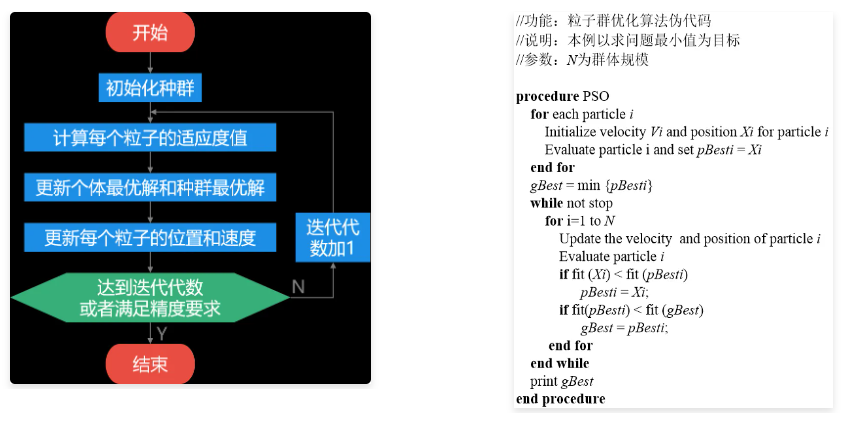
(三) 粒子群算法原理
鸟被抽象为没有质量和体积的微粒,并延伸到N维空间中。粒子i(i=1,2,…,M)在N维空间的一些参数设置如下:
- 位置表示为:
- 飞行速度表示为:
每个粒子都有一个由目标函数决定的适应度值,并且知道自己迄今为止发现的最好位置(pbest)和现在的位置,可以看做是粒子自己的飞行经验。每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest),可以看做是粒子同伴的经验。
速度更新公式:
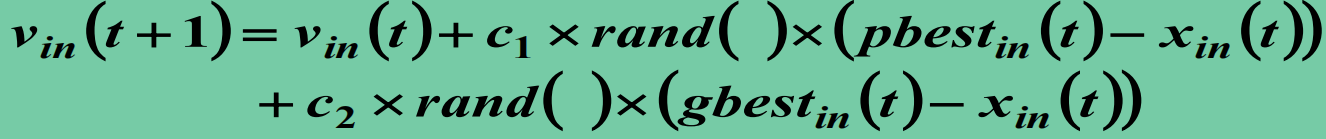
式中:
- pbest 和 gbest 分别表示粒子群的局部和全局最优位置;
分别表示粒子的序号及其维数;
为加速因子或学习因子,一般取正数;
为 [ 0, 1 ] 之间的随机数。
即每次迭代的某个粒子 i 的速度由三部分组成:
- 上一次迭代的自身速度
- 自身到自己发现的最好位置的距离乘以一个学习因子,并随机决定该项的权重
- 自身到大家发现的最好位置的距离乘以一个学习因子,并随机决定该项的权重
然后通过迭代找到最优解。在每一次迭代中,粒子通过自己和同伴的经验决定下一步的运动轨迹。
- 当 C1=0 时,粒子没有认知能力,变为只有社会的模型:
-
- 【搜索空间能力强,缺少局部搜索,因此收敛速度较快,但对于复杂问题易陷入局部最优。】

- 当c2=0时,粒子间没有交流,即没有社会信息,只有自身的认知能力,变为认知模型:
-
- 【由于个体之间没有信息交流,整个群体相当于多个粒子进行盲目的随机搜索,因此收敛速度较慢,得到最优解的可能性较小。】

(四) 全局和局部最优粒子群算法
全局和局部最优的区别主要考虑其邻域范围。
如果每个粒子的邻域是整个种群,其社会网络的拓扑结构为星状(即通信中的网孔型拓扑结构),任意两个粒子间均有联系,使得速度更新公式中的社会成分反映了种群中所有粒子的信息,即gbest是种群迄今为止发现的最好位置,则称为全局最优PSO算法。
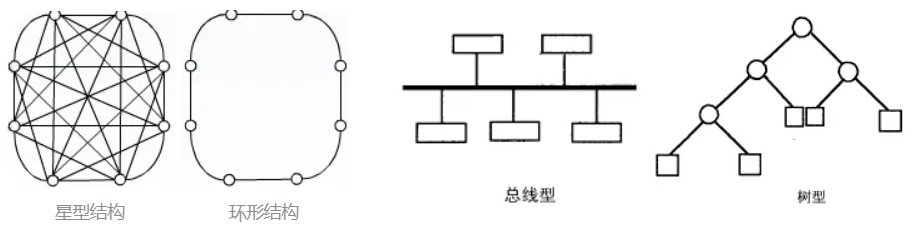
邻域较小的拓扑结构在处理复杂的、多峰值的问题上具有优势,随着邻域的扩大,算法的收敛速度将会加快,对简单、单峰值的问题有利。
(五) 惯性权重粒子群算法
1998年,Yuhui Shi对传统PSO算法进行了修正,引入了惯性权重因子(也称为动量因子),得到
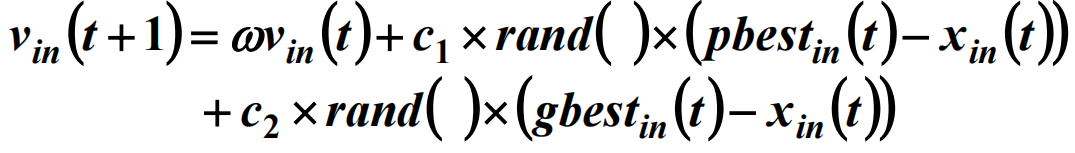
惯性权重因子的值较大,全局寻优能力强,但局部寻优能力弱;否则则反之。一般认为,惯性权重因子用于平衡全局和局部搜索能力,较大的倾向于全局搜索,较小的适用于局部搜索,因此惯性权重因子的取值应随时间逐渐减小。
实验发现,惯性权重因子取动态值能够获得比固定值更好的寻优效果。
线型递减惯性权重(Linearly Decreasing Weight, LDW)
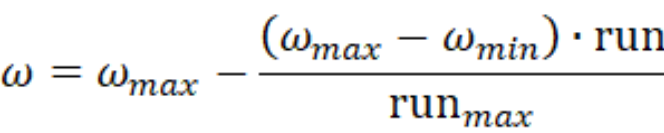
- ωmax:最大惯性权重
- ωmin:最小惯性权重
- run:当前迭代次数
- runmax:算法迭代的总次数
当迭代次数run为0时,惯性权重最大,随着迭代次数递增,惯性权重将线性递减至最小值
四、粒子群算法参数分析
PSO算法中,参数设置主要有群体规模m、粒子维数及范围、惯性因子、学习因子 、最大速率和终止条件等。
- 群体规模:种群规模m一般取20∽40,对于大部分问题10个粒子即可获得满意效果,对于比较复杂的优化问题可以取到100∽200。
- 惯性因子:惯性因子w使粒子保持运动惯性,具有扩展搜索空间的能力。当w较大时,具有较强的全局搜索能力;w较小时具有较强的局部搜索能力。当w=0时,速度只取决于当前位置和历史最好位置,速度本身没有记忆性。
- 学习因子:学习因子𝐶1和𝐶2代表每个粒子向个体和全局最优位置靠拢的程度,一般取在0∽4之间取值,大多取为𝐶1=𝐶2=2
- 最大速率:最大速率 Vmax 决定当前位置与最好位置之间的区域分辨率(精度)。如果太快,粒子有可能越过极小点;如果太慢,又有可能陷入局部极值区域,因此要适中。
- 粒子的维度:粒子维数由优化问题决定,就是问题解的长度。
- 粒子的范围:粒子范围也是由优化问题决定,每一维可以设定不同的范围。
五、粒子群算法特点
(一) 粒子群算法的特点
1. 粒子群算法的优点
- 粒子群算法没有个体的交叉、变异计算,依靠粒子速度完成搜索,迭代中只有最优的粒子将信息传递给其他粒子,搜索速度快;
- 需调整的参数较少,结构简单,易于工程实现;
- 采用实数编码,问题解的变量数直接作为粒子的维数。
2. 粒子群算法的缺点
- 不能有效解决离散及组合优化问题。
(二) 粒子群算法与遗传算法比较
1. 与遗传算法的比较相同点
- 都属于仿生算法
- 都属于随机搜索算法
- 都属于全局优化方法。在解空间都随机产生初始种群,算法在全局解空间进行搜索,且将搜索重点集中在性能高的部分
- 隐含并行性。搜索过程都是从问题解的一个集合开始的,而不是从单个个体开始,从而减小了陷入局部极小的可能性
- 根据个体的适配信息进行搜索,因此不受函数约束条件的限制,如连续性、可导性等
- 对高维复杂问题,都会存在早熟收敛和收敛性能差的问题。
2. 与遗传算法的比较不同点
- PSO算法具有记忆功能,保存好的解;而GA算法中,以前的知识随着种群的改变而被破坏。
- PSO算法中,粒子仅仅通过当前搜索到的最优点进行共享信息,所以很大程度上这是一种单项信息共享机制。而GA算法中,染色体之间相互共享信息,使得整个种群都向最优区域移动。
- PSO算法没有交叉和变异操作,粒子只是通过内部速度进行更新,因此原理更简单、参数更少、实现更容易。
- PSO算法主要用于连续问题,而GA算法除了连续问题之外,还可用于离散问题。
六、粒子群算法研究方向
- 粒子群算法自身的改进,传统粒子群算法主要适用于连续空间的函数优化,如何应用于离散空间的优化,尤其是非数值优化值得研究。
其他常见的粒子群改进算法:
-
- 混合PSO:模糊PSO、 混沌PSO、 HPSO、 免疫PSO
- 并行PSO,小生境PSO
- 二进制PSO,离散PSO
- 线性递减惯性权重,收敛因子,最大速度,规范系数
- 粒子群算法的参数设置对算法性能影响很大,如何通过对参数的自适应调整提高算法性能有待进一步研究。
- 粒子群算法的稳定性和收敛性研究虽取得一定成果,但还需进一步深入研究。
- 粒子群算法与其他优化的融合也是一个值得进一步研究的课题。
- 粒子群算法的信息共享机制提高了算法的收敛速度,进一步研究信息共享机制(如拓扑结构),在保证算法收敛速度的基础上,提高算法的全局搜索能力。
八、粒子群算法求解空间信息问题
(一) 避障与路径规划问题
以典型的空间信息问题——路径规划问题描述粒子群算法流程:
如图,给定环境信息,如果该环境内有障碍物,通过一定的搜索策略寻找到一条从起始点到目标点的最短路径,并且路径不能与障碍物相交。如图所示,给出了起点 s(遥感信息工程学院)、终点 t(信息学部二食堂)和三处障碍分布:
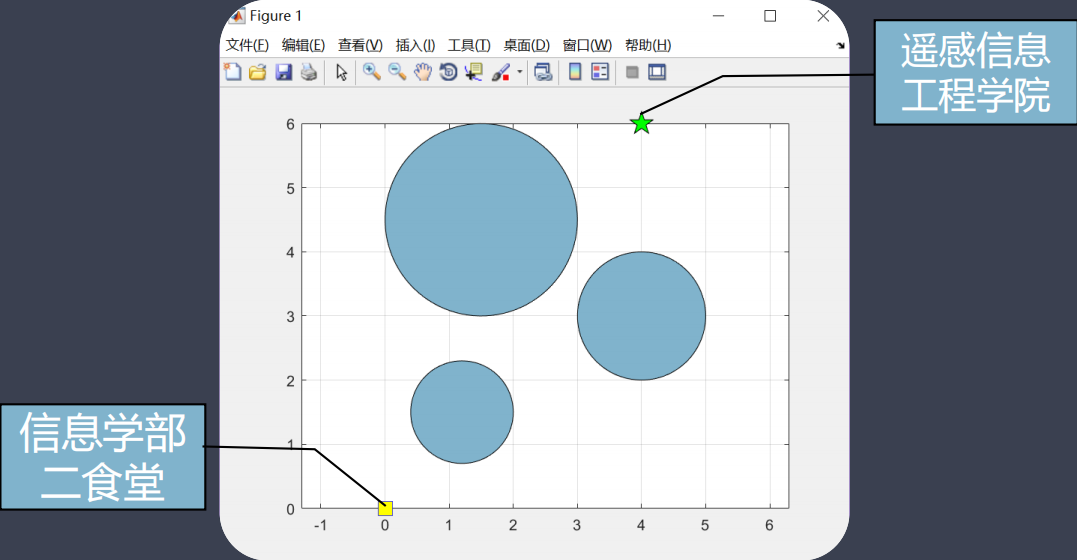
路径规划问题求解思路:
1. Step1:随机初始化150个微粒,粒子结构由5部分组成。
粒子的位置和速度用浮点数随机生成,位置范围[-10,10],速度统一设为0。初始化后某个粒子的结构为:
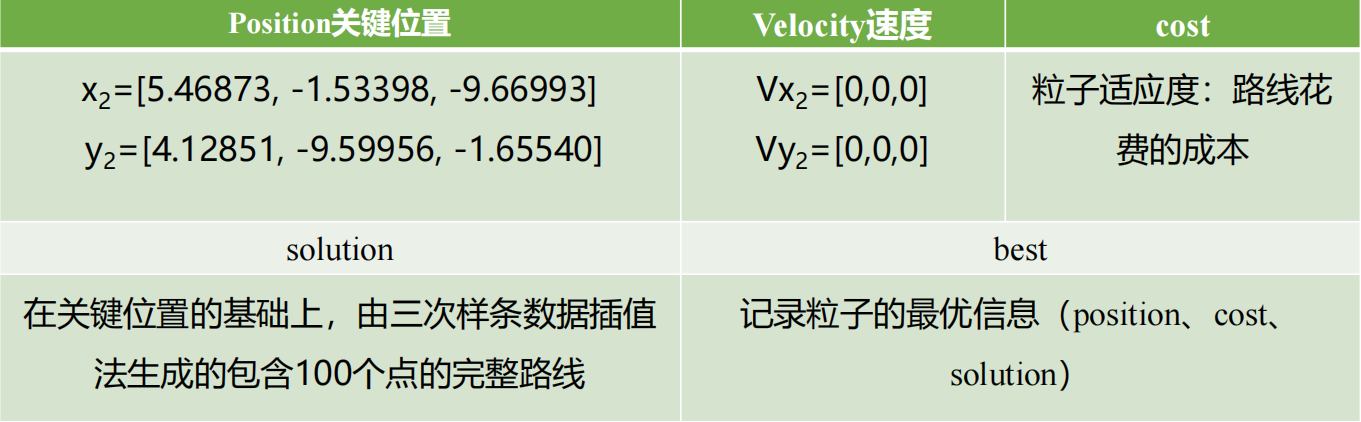
每个粒子包含三个关键位置坐标,然后根据这三个关键位置坐标,由三次样条数据插值生成一条包含100个点的路线,评估粒子的适应度就是评价这条路线的成本。
粒子在迭代运动的过程,实际上就是不断挪动路线的过程,最终找到一条最合适的路线。
2. Step2:初次评价每个微粒的适应度值
粒子的适应度评价函数必须能够表明该粒子对应路线的花费成本,在路径规划问题中则包括路线距离成本和障碍物碰撞成本。其数学公式表示为:
式中:
- xx、yy 是路线中的插值点坐标
- dx、dy 分别是 xx、yy 之间的差
- Distance 代表路线距离成本,即路线上各点之间距离之和
- Violation 是碰撞成本
- Xobstacle、Yobstacle、Robstacle 是障碍物的圆心坐标和半径
- cost 是总成本
- 若点在障碍物内,则
小于 1。
上述该粒子的评价结果:

3. Step3:初次寻找个体最优和群体最优。
将每个微粒的适应度值与历史最好位置pbest进行比较,如果较好则将其作为当前的最好位置pbest。
将每个微粒的适应度值与种群的最好位置gbest进行比较,如果较好则将其作为种群的最好位置gbest。
当前该粒子历史最优和群体最优粒子的关键位置为:
x2=[5.46873, -1.53398, -9.66993] xgbest(0)=[7.195211, 6.21946, 4.58892]
y2=[4.12851, -9.59956, -1.65540] ygbest(0)=[-0.40904, -1.16302, 5.51960]
4. Step4:根据速度和位置公式调整粒子的飞行速度和所处位置粒子将通过下面的公式更新自己的速度和位置
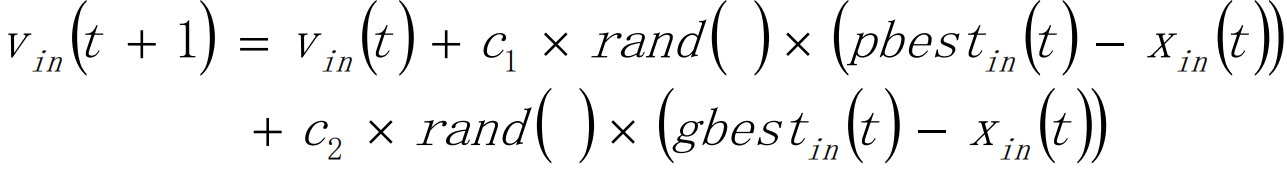
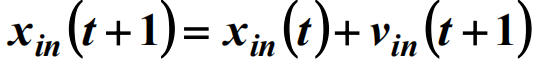
- 式中,i=1,2,⋯ ,M; n=1,2⋯ , 𝑁𝑁 分别表示粒子的数量及其维数;C1、C2 为加速因子或学习因子,一般取正数;rand() 为[0,1] 之间的随机数;
- 速度和位置均设定最大值,超过边界值时取边界值。
在速度更新公式中:
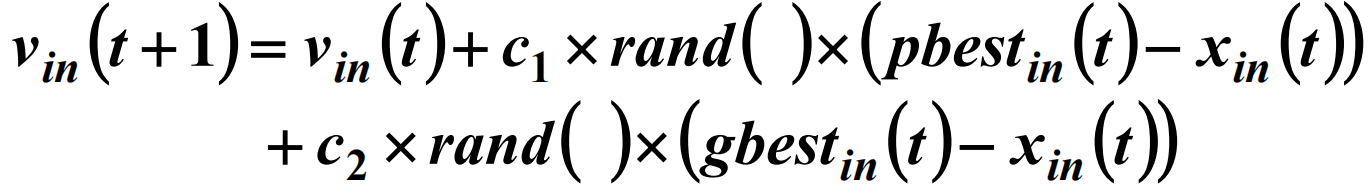
第一项称为记忆项,表示上次速度大小和方向的影响;
第二项称为自身认知项,是从当前点指向粒子自身最好点的一项,表示粒子的动作来源于自身的经验;
第三项称为群体认知项,是一个从当前点指向种群最好点的项,反映了粒子间的协同合作和知识共享。
总之,粒子的速度更新公式由认知和社会两部分组成,粒子就是通过自身的经验和同伴间最好的经验来决定下一步的运动轨迹。
本例中速度的范围设定在[-2,2],加速因子c1=c2=1.5。
当前该粒子和群体最优粒子的关键位置为:
- x2=[5.46873, -1.53398, -9.66993]
xgbest(0)=[7.195211, 6.21946, 4.58892] - y2=[4.12851, -9.59956, -1.65540]
ygbest(0)=[-0.40904, -1.16302, 5.51960]
那么第1次迭代该粒子的速度更新为:
- Vx2(1)=0+1.5*rand*([5.46873, -1.53398, -9.66993]-[5.46873, -1.53398, -9.66993])+1.5*rand*([7.195211, 6.21946, 4.58892]-[5.46873, -1.53398, -9.66993])
=0+0+[0.32249, 2.36630, 14.21790]
=[0.32249, 2, 2] - Vy2(1)=0+1.5*rand*([4.12851, -9.59956, -1.65540]-[4.12851, -9.59956, -1.65540])+1.5*rand*([-0.40904,-1.16302,5.51960]-[4.12851, -9.59956, -1.65540])
=0+0+[-2.66725, 7.76289, 10.25179]
=[-2, 2, 2]
位置更新公式:
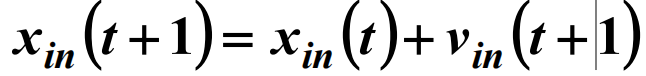
第1次迭代该粒子的位置更新为:
- X2(1)=[5.46873, -1.53398, -9.66993]+[0.32249, 2, 2]
=[5.79122, 0.46601, -7.66993] - Y2(1)=[4.12851, -9.59956, -1.65540]+[-2, 2, 2]
=[2.12851, -7.59956, 0.34459]
至此第1次迭代中所有粒子的速度和位置更新完毕。
5. Step5:再次用成本函数评估所有粒子适应度并找到个体历史最优位置和群体最优位置。
- 此时该粒子的适应度是96.89413。
- 该粒子的历史最优位置更新为:
-
- X2(1)=[5.79122, 0.46601, -7.66993]
- Y2(1)=[2.12851, -7.59956, 0.34459]
将每个微粒的适应度值与粒子群的最好位置gbest进行比较,如果较好则将其作为粒子群的最好位置gbest。粒子群的适应度值如下表:
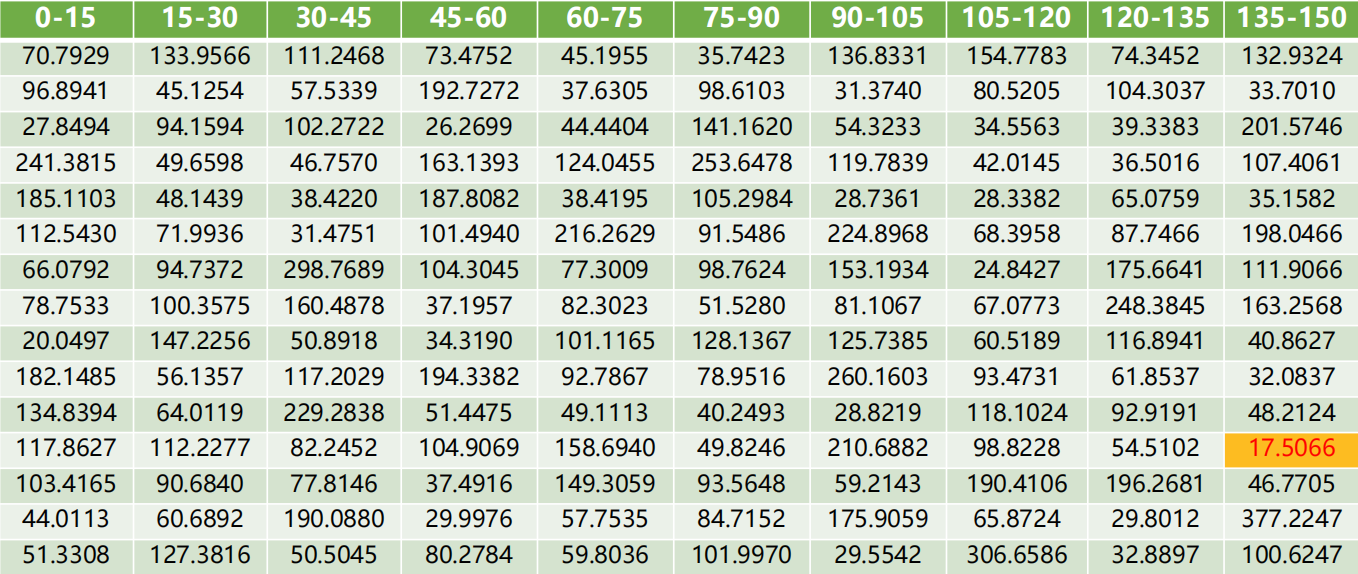
此时粒子群最优个体适应度=cost=17.50662,最佳位置是:
- Xgbest(1)=[-3.58667, -3.09023, 1.28120]
- Ygbest(1)=[0.11205, 1.26872, 6.86129]
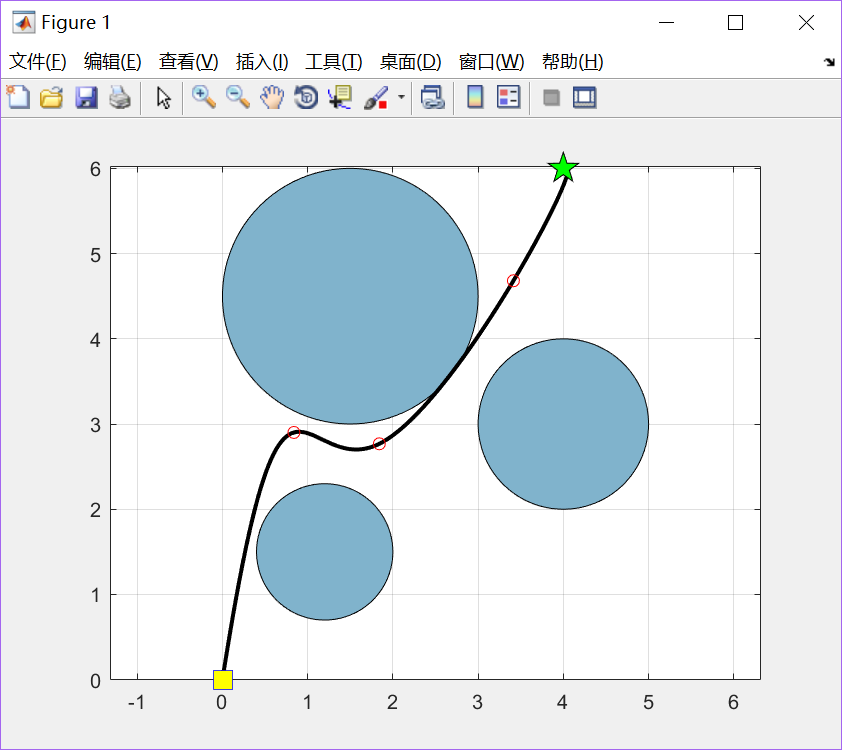
绘出第一次迭代后的群体最优路线,3个红圈标记处代表该粒子的关键位置Xgbest(1)和 Ygbest(1)
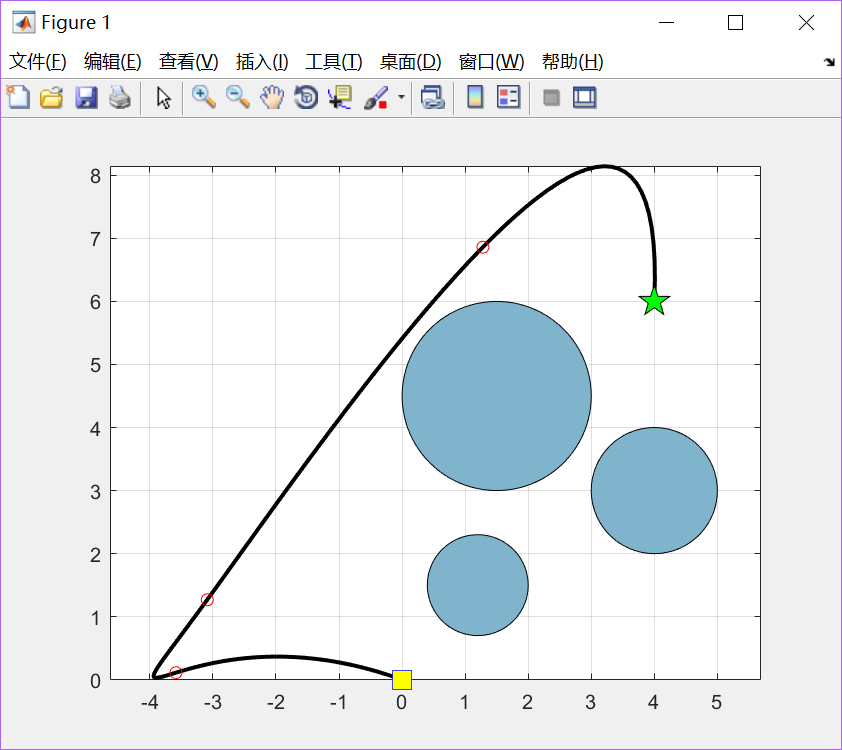
6. Step6:判断迭代次数是否达到500,若未达到转到Step4。
第2次迭代后150个粒子的适应值:
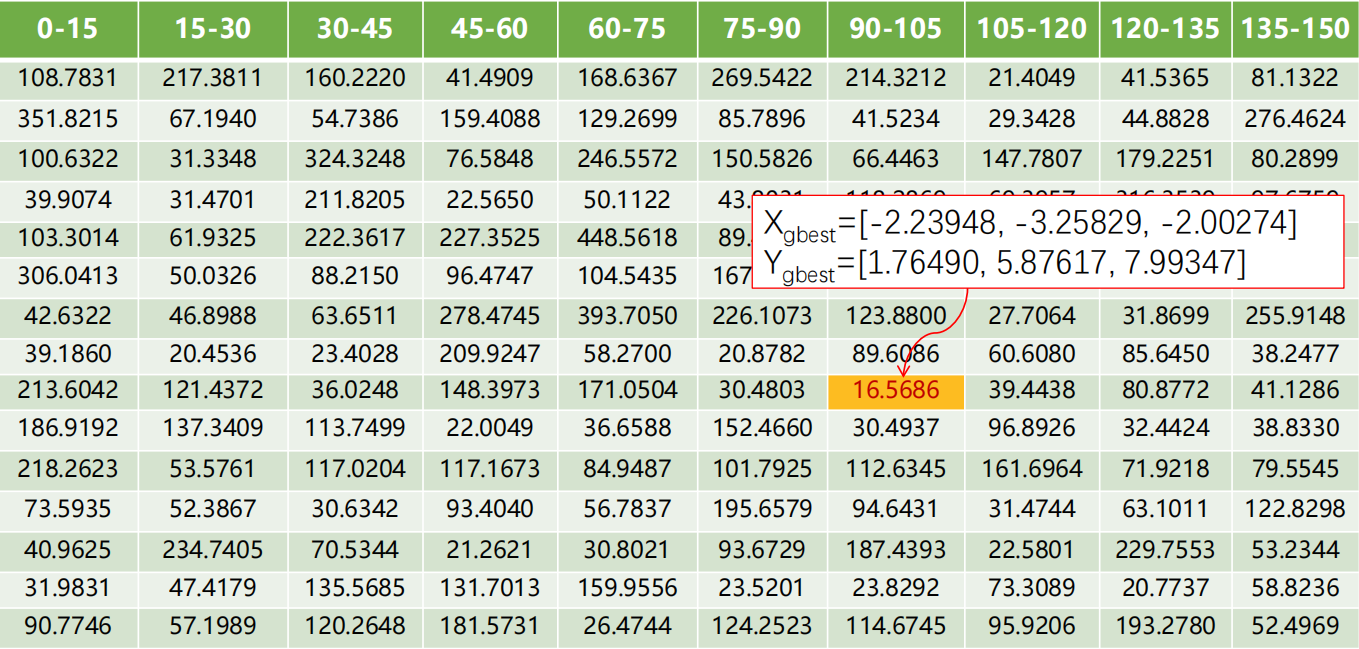
第500次迭代后150个粒子的适应值:
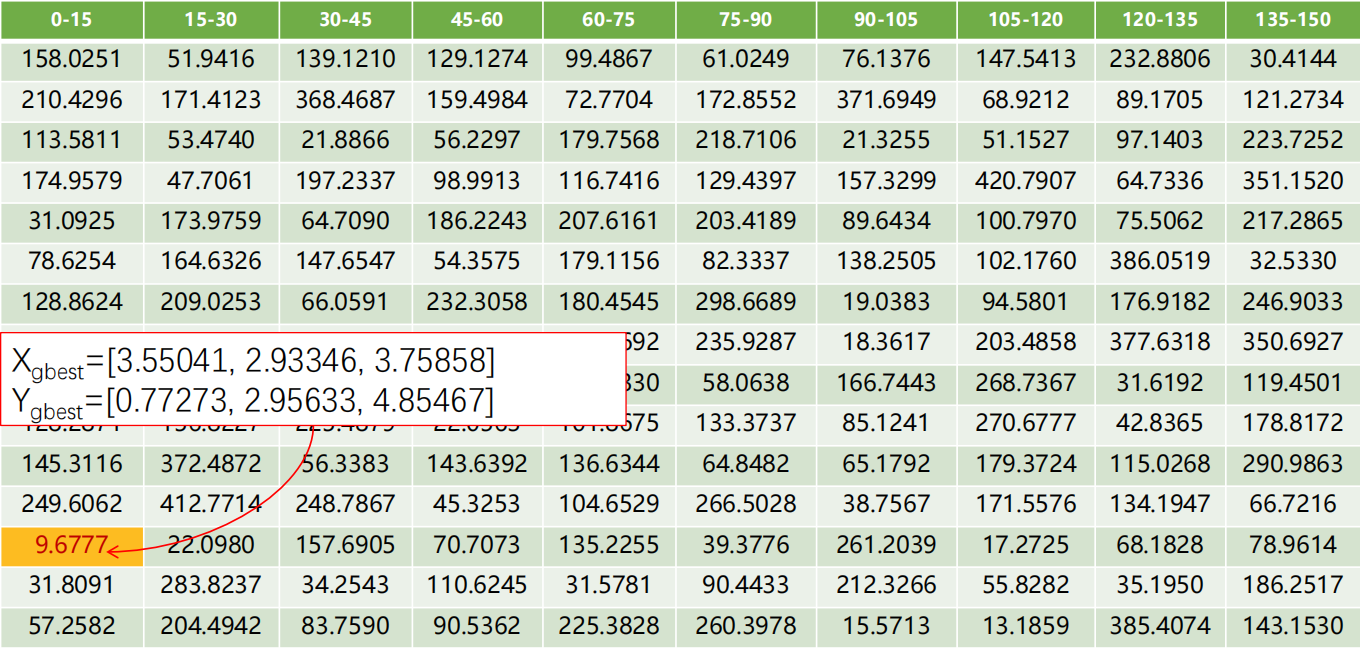
7. 迭代结束后群体最优值:
- Xgbest=[0.83880, 1.84098, 3.41410]
- Ygbest=[2.90110, 2.76811, 4.68080]
- cost=8.2765
(二) 旅游路径规划问题
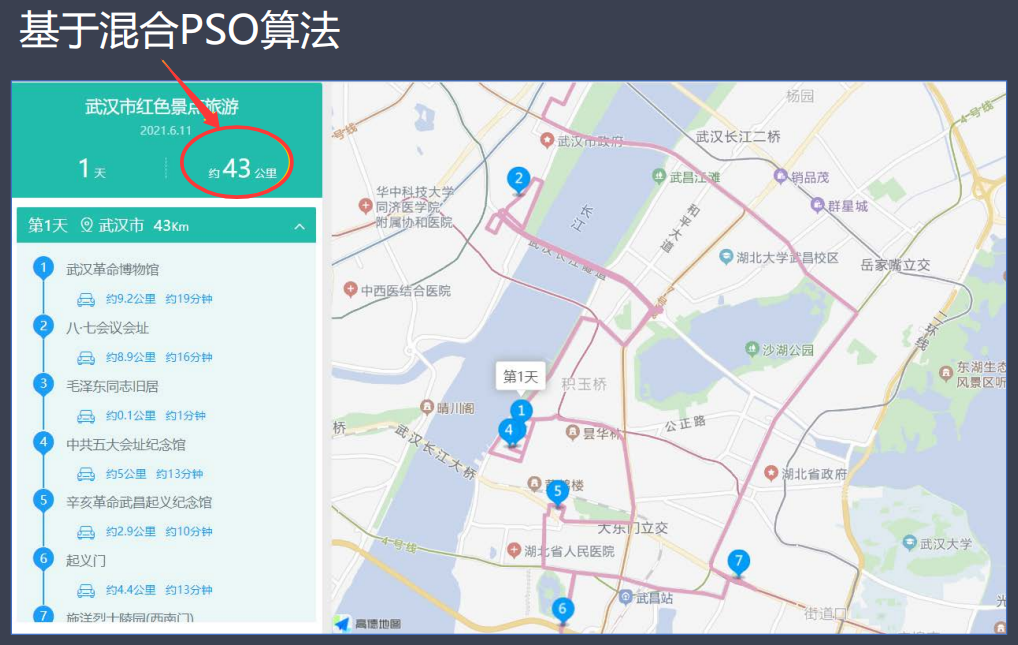
武汉革命博物馆-八七会议会址纪念馆-毛泽东同志旧居-中共五大会址纪念馆-辛亥革命武昌起义纪念馆-武昌起义门旧址-施洋烈士陵园-汉口新四军军部旧
基于混合粒子群的旅游路径规划问题求解:
标准粒子群算法通过追随个体极值和群体极值完成极值寻优,虽然操作简单,且能够快速收敛。但是随着迭代次数的不断增加,在种群收敛集中的同时,各粒子也越来越相似,可能在局部最优解周边无法跳出。混合粒子群算法摒弃了传统粒子群算法中的通过跟踪极值来更新粒子位置的方法。而是引入了遗传算法中的交叉和变异操作,通过粒子同个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解。
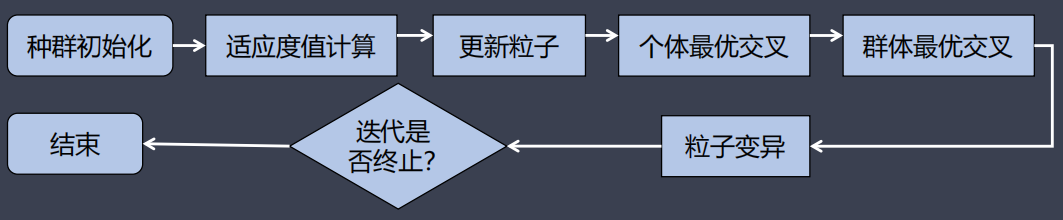
- 根据粒子适应度值更新个体最优粒子和群体最优粒子;
- 个体最优交叉把个体和个体最优粒子进行交叉得到新粒子;
- 群体最优交叉把个体和群体最优粒子进行交叉得到新粒子;
- 粒子变异是指粒子自身变异得到新粒子。
1. 粒子定义
粒子Xi 是由1到m共m个数字随机排序组成的长度为m的向量。
2. 适应度值表示
适应度值用遍历路径的长度表示
3. 交叉操作
首先选择两个交叉位置,然后把个体和个体极值或个体与群体极值进行交叉,假定随机选取的交叉位置为3和5,操作方法如下:
个体:

极值:

交叉新个体:

对重复的城市进行调整:

交叉操作MATLAB实现:

4. 变异操作
变异方法采用个体内部两位互换方法,首先随机选择变异位置pos1和pos2,然后把两个变异位置互换,假设选择的变异位置为2和4,变异操作如下所示:
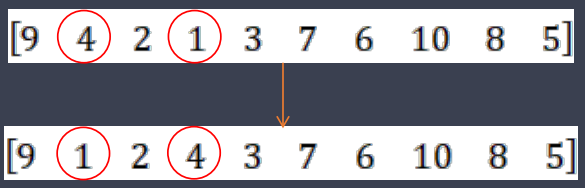
对得到的新个体采用保留优秀个体策略,只有当新粒子适应度值好于旧粒子时才更新粒子。
变异操作MATLAB实现:

5. 运行结果
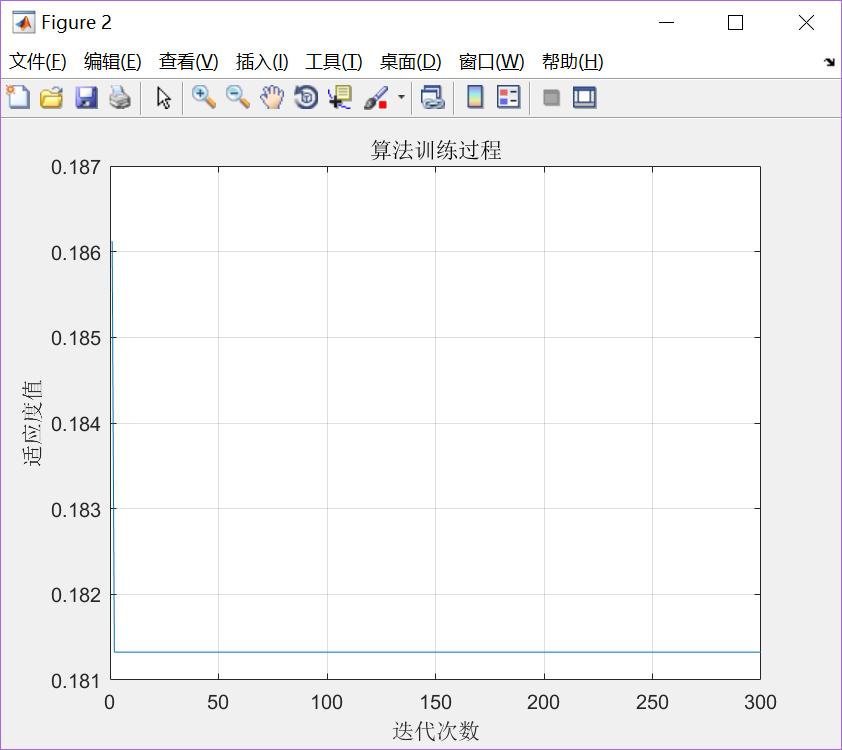
最佳路线:7->8->2->1->4->3->5->6->7
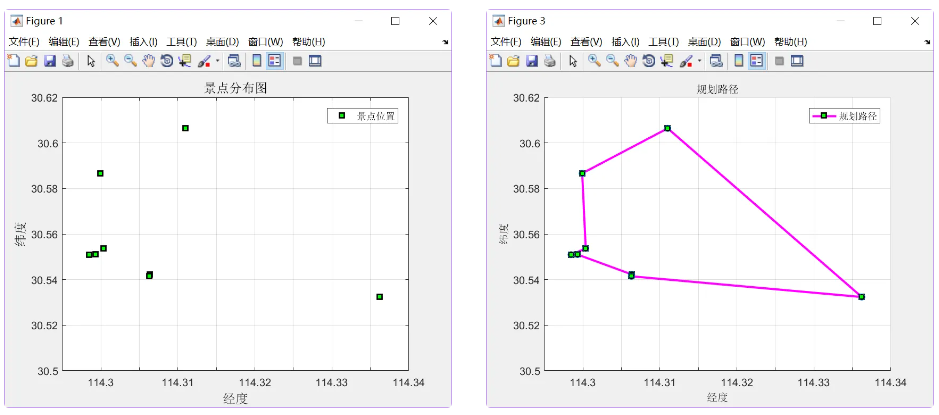
迭代次数 = 300; 最短距离 = 0.1813° ≈ 20.091km
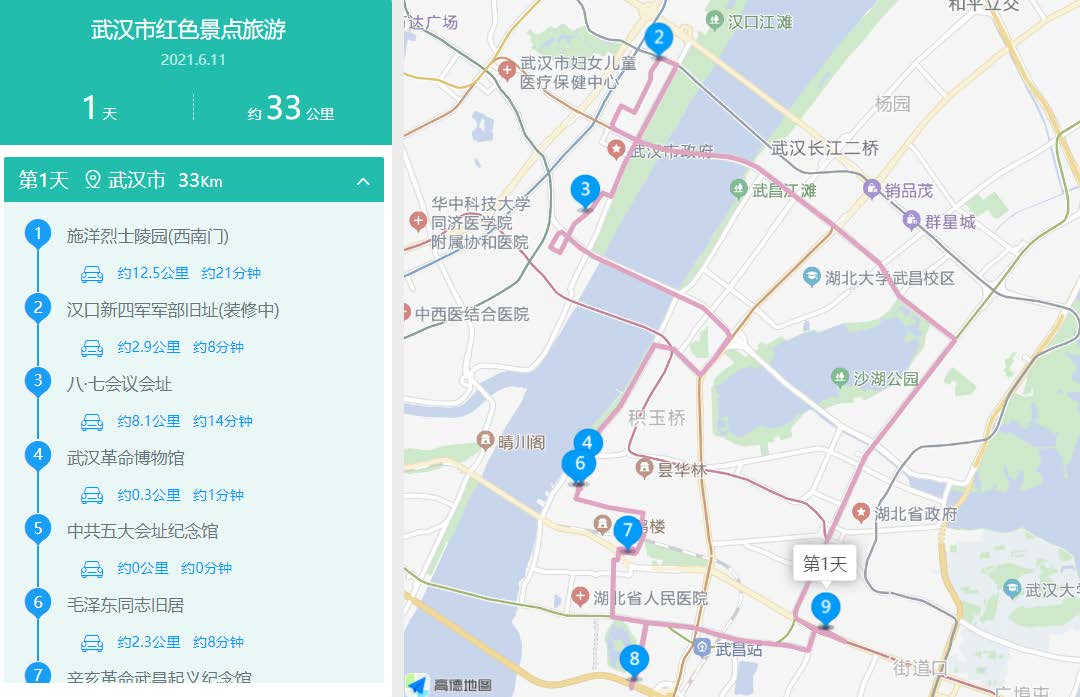
该运行路线对应的景点顺序是:
起点:施洋烈士陵园->汉口新四军军部旧址->八七会议会址纪念馆->武汉革命博物馆->中共五大会址纪念馆->毛泽东同志旧居->辛亥革命武昌起义纪念馆->武昌起义门旧址->终点:施洋烈士陵园。






















 1022
1022

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










