一、遗传算法的产生
(一) 遗传算法的产生历程
- 早在50年代,一些生物学家开始研究运用数字计算机模拟生物的自然遗传与自然进化过程;
- 1963年,德国柏林技术大学的I. Rechenberg和H. P. Schwefel,做风洞实验时,产生了进化策略的初步思想;
- 60年代,L. J. Fogel在设计有限态自动机时提出进化规划的 思想。1966年Fogel等出版了《基于模拟进化的人工智能》,系统阐述了进化规划的思想;
- 60年代中期,美国Michigan大学的J. H. Holland教授提出借鉴生物自然遗传的基本原理用于自然和人工系统的自适应行为研究和串编码技术;
- 1967年,他的学生J. D. Bagley在博士论文中首次提出“遗传 算法(Genetic Algorithms)”一词;
- 1975年,Holland出版了著名的“Adaptation in Natural andArtificial Systems” ,标志遗传算法的诞生;
- 70年代初,Holland提出了“模式定理”(Schema Theorem),一般认为是“遗传算法的基本定理”,从而奠定了遗传算法研究的理论基础;
- 1985年,在美国召开了第一届遗传算法国际会议,并且成立了国际遗传算法学会(ISGA,International Society of Genetic Algorithms);
- 1991年,L. Davis编辑出版了《遗传算法手册》,收编了遗传算法在工程技术和社会生活中大量的应用实例。
(二) 与GA相关的重要学术期刊与国际会议
1. 重要学术期刊:
- IEEE Transactions on Evolutionary Computation
- Evolutionary Computation
- …
2. 重要国际会议:
- International Conference on Genetic Algorithm
- ACM Genetic and Evolutionary Computation Conference
- Workshop on Foundations of Genetic Algorithms and
- Classifier Systems
- Genetic Programming Conference
- International Workshop on Artificial Life
- ……
二、遗传算法基本结构
Holland所提出的遗传算法常被称为简单遗传算法(SGA),这是一种基本的遗传算法,其遗传进化操作过程简单,容易理解,是其它一些遗传算法的雏形和基础。
基本遗传算法的组成:
- 编码(产生初始种群)
- 适应度函数
- 遗传算子(选择、交叉、变异)
- 运行参数

三、遗传算法实例
考虑下面的优化问题:
【要求解的精度为小数点后4位】
上面这个函数就是我们要优化的目标,即求解 的最大值,所以称为“目标函数”。
目标函数的三维图形如下图所示:
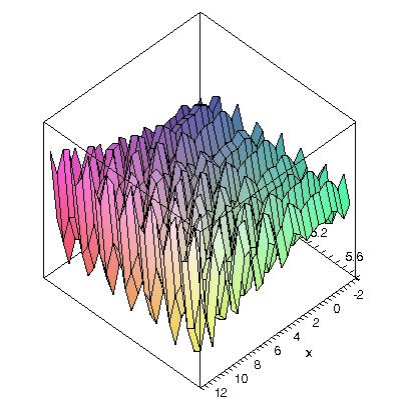
(一) 步骤1. 个体的编码
问题的可能解为实数对 的形式。这里首先将每个变量编码为二进制位串,然后将表示各个变量的二进制数串连接起来便得到问题可能解的一种表示。表示每个变量的二进制位串的长度取决于变量的定义域和所要求的精度。
让我们来一步一步理解编码的过程:
1. 假设 ,所要求的精度为小数点后 t 位。这要求将区间划分为至少
份。
- 为什么要这样划分呢?让我来慢慢给你讲。
- 例如在该问题中,
,要求解的精度为小数点后4位,也就是说,如果我想在这个区间里找到一个最优解,我就得从
开始,每次增加 0.0001,即
直到
,分别将这么多数依次代入到目标函数中,看看哪个数的结果最好。
所以我们就至少要将
分为
份。
- 为什么说是至少呢?因为题目要求的精度是小数点后4位,我们当然也可以分为更多份,以获得更高的精度,但对于解决这道题来说,就不是很有必要啦。
- 同理,因为
,所以我们可以知道
的区间至少划分为
份。
2. 假设表示变量 的二进制位串
的长度用
表示,则
可取为满足下列不等式的最小整数 m:
,即有
。
- 怎么理解这一步呢?
- 例如我们刚刚计算出来
要分为 151000 份,那相应的,
的二进制编码就至少需要有 151000 种变化方式。
我们知道对于二进制数来说,1 位的二进制数有 2 种组合,2 位的二进制数有 4 种组合……17 位的二进制数有 131072 种组合,18 位的二进制数有 262144 种组合。诶,我们发现 17 位没办法满足 151000 种变化,而 18 位可以,所以
的二进制编码至少需要有 18 位!
按照这个思路,将求编码位数的过程转换成通用公式应该是
,诶?怎么和上面的公式不太一样?为什么上面的公式里有个减一?
试想如果
,精度为整数,即保留小数点后0位,那么按照之前的思路计算,我们应该将区间分为
份,但是实际上可能的解应该是 1、2、3、4、5,一共五个,这是因为在计算 (5-1) 的时候实际上计算的是两个数之间的差距,就像从一楼到五楼爬了几层楼,而我们需要计算的是从一楼到五楼一共有几层楼?因此计算出来需要划分的分数应该加上一个1才是合理的,即
份。
所以计算二进制数位数的公式就变成了
也就是上面写出来的形式啦。
由此,我们可以计算出来表示变量
的二进制位串的长度为
,表示变量
的二进制位串的长度为
。
表示问题解的二进制位串如下图所示:(其中前18位表示变量
,后15位表示变量
)
3. 将 的二进制表示转换回十进制可按下式计算:
其中
表示变量
的二进制子串
对应的十进制数。
例如给定下列 33 位二进制位串:010001001011010000111110010100010
那么前 18 位所表示的变量
的值为:
而后 15 位所表示的变量
的值为:






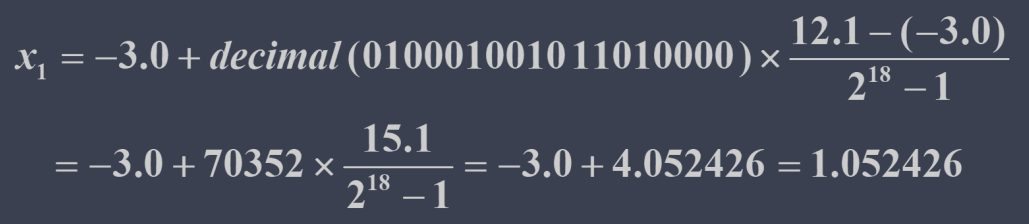
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 23万+
23万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










