突触延迟的论文阅读

关于昨天的昨天我还没有比较好的思路，看别人推荐了一篇论文如下

Maintaining Causality in Discrete Time Neuronal Network Simulations

目录

Maintaining Causality in Discrete Time Neuronal Network Simulations

abstract

1 Introduction

2 Networks with Discrete Spike Times

2.1 Networks without Propagation Delays

2.2 Networks with Propagation Delays

3 Networks with Continuous Spike Times

4 Distributed Networks

5 Conclusions and Perspectives

abstract

在设计神经元网络的离散时间仿真工具时，在定义神经元的连续动态和它们交换的点事件(尖峰)之间的相互作用时经常遇到概念上的困难。当该工具被设计为分布在许多计算机上时，这些问题就会显著增加。在本章中，我们汇集了过去几年来为处理这些困难而发展起来的方法。我们描述了一个框架，在这个框架中，模拟中的事件的时间顺序保持一致。它适用于具有任意亚阈动态的神经元网络，具有或不具有延迟，交换点事件约束于离散时间网格或连续时间网格，并且与分布式计算兼容。

1 Introduction

神经网络模拟对于计算神经科学的发展至关重要，因为非线性活动动力学只能部分地通过纯分析方法获得，而实验技术在观察和操纵大量神经元的能力方面仍然受到严重限制。大脑是一个不寻常的物理系统，因为它由元素(神经元)组成，这些元素可以用一组微分方程来描述，但这些元素之间的相互作用是由点状事件(动作电位或尖峰)介导的。此外，它是一个非常复杂的系统——例如，皮层中的每个神经元接收来自其他神经元的大约10^4个连接，这些连接既有来自其直接区域的神经元，也有来自大脑较远区域的神经元。模拟这种复杂程度的网络自然意味着使用分布式计算技术。然而，连续时间动力学和离散时间通信的网格化使得为动力学集成定义一个一致且足够通用的框架非常困难。

有两种经典的模拟方法:时间驱动和事件驱动。前者定义了一个计算时间步长h。模拟的一次迭代涉及每个神经元在一个时间步长上推进其动态。如果满足产生动作电位的条件，则向它投射到的每一个神经元。当所有神经元都被更新后，下一次迭代开始。在后一种方法中，事件队列管理发送峰值的顺序。每个神经元只有在接收到一个事件时才会更新。如果满足生成动作电位的条件，则将新事件插入队列。这种算法可以非常简单地定义，并且在神经元动力学是可逆的情况下非常有效——例如，如果尖峰的到来导致膜电位立即跳跃，然后呈指数衰减。在这种情况下，神经元只能在传入事件到达时触发，因此神经元在一个事件到达和下一个事件到达之间的行为与网络的正确整合无关。对于具有不可逆动力学的神经元模型，例如那些膜电位的最大偏移发生在峰值到达后的一段时间的模型，定义事件驱动算法要困难得多。需要更复杂的机制:例如，神经元可能会在接近触发条件时将临时事件放在队列中，但可能必须在进一步事件到达时修改其预测的峰值时间[1,2]。在下文中，我们将重点关注上述定义的时间驱动方法，该方法可以在不改变更新和尖峰传递算法的情况下合并任何类型的亚阈值动态，并且在模拟大规模神经元网络方面具有良好的性能，并且在分布式时具有出色的扩展性[3]。

在这里，我们提出了一个框架，该框架定义了神经元之间的相互作用，而不破坏因果关系，即神经元更新的顺序不会影响模拟的结果。该框架适用于分布式计算。在第10.2节中，我们将介绍连续时间神经元元素之间点事件相互作用的基础知识。我们首先讨论了具有历史意义的无传播延迟的神经元网络概念，并描述了一种更新方案，确保仿真结果与神经元更新的顺序无关(第10.2.1节)。然后，我们演示了如何调整该方案以纳入计算时间步长h的倍数的延迟(第10.2.2节)。这种网络传统上将峰值时间限制在离散时间网格上。但是，对于传播延迟大于或等于计算时间步长的网络，可以放宽此约束。在10.3节中，我们将展示如何扩展该方案以允许神经元生成和接收离网点事件。最后，我们讨论了如何利用神经元之间的传播延迟来优化分布式环境中机器之间的通信效率(第10.4节)。

2 Networks with Discrete Spike Times

在下面，我们将假设神经元之间的通信是由突触介导的。当一个神经元出现峰值时，它所有的输出突触都会向各自的突触后神经元发送一个离散的事件。事件是参数化权值w，由突触后神经元根据其实现的突触后动态进行解释。例如，突触后神经元可以将w解释为其膜电位瞬时跳跃的大小，或作为α函数实现的突触后电流的最大振幅(参见第1章)。在第10.2.2节中，事件进一步通过整数延迟k参数化，它以计算时间步长h为单位表示神经元之间的传播延迟d，即d = k·h。

2.1 Networks without Propagation Delays

考虑以下情况:神经元i和神经元j具有很强的互抑连接，这样一个脉冲会导致突触后神经元的膜电位瞬间降低。每个神经元都接受足够的输入来驱动它在时刻t产生尖峰。如果神经元i首先更新到时刻t，那么尖峰会立即传递给神经元j。当j被更新时，强抑制会阻止膜电位通过阈值，因此它本身不会产生尖峰。相反，如果先更新神经元j，则神经元j在时间t出现峰值，神经元i受到抑制。

上面示例中的顺序依赖是非常不可取的。然而，通过一个小的概念调整，模拟可以在内部保持一致。惯例是定义一个尖峰的产生只可能受到它之前的尖峰的影响。这在图10.1(a)的流程图中描述。当神经元从t更新到t + h时，它首先根据上游神经元在时间t(算子G)发射的新峰值修改其状态，例如增加膜电位或突触后电流。然后进行亚阈动态，将修改后的神经元状态(包括新事件)传播到t+h(算子Fh)。此时，应用峰值标准;如果它们被满足了，神经元就会发出一个脉冲。因此,飙升的影响神经元状态符合接收t,可以看到在神经元膜电位在图10.1 (b),但最早的时候能发出一种冲动的结果收到t + h上升。这相当于考虑峰值无穷小Χ延迟,使模拟的效果一致,在更新的顺序并不影响结果。在我们之前的两个神经元相互抑制的例子中，两个神经元都将在时间t放电。假设没有不应期，相互抑制的作用将导致两个神经元在时间t + h超极化

2.2 Networks with Propagation Delays

最小的延迟

将第10.2.1节中描述的算法更改为网络中所有传播延迟等于计算量的算法是特别简单的实际上，它只是改变了两个算子Fh和G的阶数，如图10.1和图10.2所示。如果神经元在时间t预峰值，这个峰值立即被传递到神经元后(图10.2(b))。当神经元post从t更新到t+h时，首先执行亚阈值动态将神经元传播h步(算子Fh)，然后修改神经元状态以包含t+h时可见的新事件，包括神经元pre发送的尖峰。请注意，对于这种情况和假设没有传播延迟的情况，模拟的基础结构是相同的。在时间t产生的尖峰被立即传递到它的目标，但由于不同的操作顺序，尖峰的影响在第一种情况下是瞬时的，但在第二种情况下延迟了h。

图10.1。无传播延迟的离散时间仿真示意图:(a)神经元更新算法。该流程图描述了将单个神经元的状态y传播一个时间步长h所需的操作顺序。算子G根据传入的事件修改状态，算子Fh执行亚阈值动态;(b)脉冲传递及其对突触后神经元的影响。神经元的膜电位Vpre在时间步长(t−h, t)内越过阈值θ，因此在时间t发出一个尖峰，膜电位复位为V0。脉冲到达神经元后没有延迟(锯齿形箭头)。填充的圆圈表示在一个时间步长结束时神经元可以报告的膜电位值。膜电位的中间值(不可观察的)显示为未填充的圆圈

图10.2。具有传播延迟的离散时间仿真示意图:(a)神经元更新算法。该流程图描述了将单个神经元的状态y传播一个时间步长h所需的操作顺序。算子Fh应用亚阈值动态，算子G根据传入的事件修改状态。注意，这两个操作的顺序与图10.1所示的顺序相反;(b)脉冲传递及其对突触后神经元的影响。如图10.1(b)所示，神经元在时间t预发射一个尖峰。尖峰以最小的延迟h(锯齿形箭头)到达神经元后。填充的圆圈表示在一个时间步长结束时神经元可以报告的膜电位值。膜电位的中间值(不可观察的)显示为未填充的圆圈

用于存储挂起事件的数据结构可以非常简单。如果所有的突触都有相同的动态，只是振幅不同，那么每个神经元只需要一个缓冲区来存储传入的事件。只需要一个缓冲的神经元模型的例子是那些突触相互作用的模型,使膜电位瞬间增加，或诱发指数型突触后电流。其他神经元模型可能有不止一组突触动力学，例如抑制性相互作用的时间常数比兴奋性相互作用的时间常数长。显然，在这种情况下，每个时间常数需要一个缓冲区。然而，为了简单起见，我们将只关注一组突触动力学的神经元模型.

根据实现的不同，单元素或双元素缓冲区都足以维持系统中的因果关系。如果全局调度算法对所有神经元进行两次迭代——一次推进动态，第二次应用峰值标准并传递任何生成的事件——那么一个元素的缓冲区就足够了，因为“读”和“写”阶段是完全分开的。然而，出于缓存有效性的原因，最好只迭代一次所有神经元，即对于每个神经元，推进其动态，应用其峰值标准，并在峰值时传递新事件。在这种情况下，“读”和“写”阶段不再被清晰地分开，并且需要一个双元素缓冲区。

双元素缓冲器如图10.3所示。缓冲区的一侧可以被认为是“读”侧，另一侧作为“写”侧。当神经元i修改其状态以合并新事件(图10.2中的算子G)时，它收集在t + h从“读”侧可见的求和权重。读取动作清除了缓冲区的这一边。如果任何投射到i的神经元在t + h发出尖峰，则该事件的权重被添加到“写”端。在所有神经元都被更新后，它们的所有缓冲区都被切换，所以空的“读”侧现在是“写”侧，而“写”侧，包含那些在t + 2h时可见的事件，现在是“读”侧。因此，神经元更新的顺序不会影响结果，因为在一个时间步中产生的事件总是与下一个时间步中产生的事件完全分开。

对于没有传播延迟的网络，可以使用完全相同的结构，只是对缓冲元素的时间分配移动了h:在图10.3(a)中，左侧接收时间步长t + h的事件，而在时间步长t中可见的事件的加权总和从右侧读出。

General Delay

通过将简单的双元素缓冲区替换为环形缓冲区，可以将模拟具有最小传播延迟h的网络的系统转换为包含许多不同延迟的系统，只要它们都是h的整数倍。传统的环缓冲区是队列的实现。数据用连续的段序列表示。新元素被添加到序列的一端，而最老的元素从另一端弹出。

图10.3。(A)在时间步长(t, t + h)中，缓冲区的灰色边是“写”边，它将在此时间步长中生成的事件的权重求和，这些事件将在下一步中可见。缓冲区的白色一侧是“读”侧，包含在前一个时间步中接收到的所有事件的加权求和，Σiwt+h i。一旦神经元读出缓冲区，“读”端就被清空;(b)所有神经元更新后，切换神经元缓冲区。现在，空白的白色部分接收新的事件，灰色部分由神经元读取，因为它从t + h更新到t + 2h

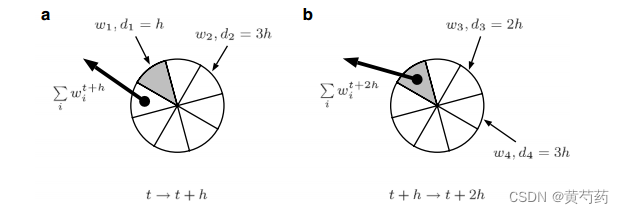
图10.4。随机存取环缓冲区,适用于网络延迟的整数倍h。权重wi的事件写入部分相应延迟di,这样延迟d = k·h对应段k以及从当前位置:阅读(一)时间步(t, t + h]:读取缓冲区的位置包含总结的部分重量的所有事件成为可见的t + h;(b)时间步长(t + h, t + 2h):读取位置已移动到下一段(灰色)，其中包含在t + 2h时可见的所有事件的权值之和

因此，可以想象包含数据的弧在添加和删除数据时围绕环旋转。通过这种方式，可以实现队列，而不必不断分配新内存。出于我们的目的，我们需要更像随机访问环缓冲区的东西，如图10.4所示(参见[3])。环的每一段对应一个时间步长。当神经元从t更新到t+h时，它从包含在t+h时可见的事件的总权重的段中读取，然后清除该段。根据传入事件的延迟将其分类到其他段中:延迟为k·h的尖峰将从当前读取位置开始分类到第k段。在所有神经元都被更新后，所有缓冲区的读取位置围绕一个段移动。如果要保持正确的事件顺序，环形缓冲区需要适当的大小——它必须足够大，以适应模拟系统中神经元之间最大的传播延迟，dmax = kmax·h，而不需要“包裹”。因此，缓冲区的最佳大小是kmax + 1。根据实现的不同，dmax可以在创建网络之前指定，也可以在创建网络时动态确定。

3 Networks with Continuous Spike Times

在上面讨论的系统中，尖峰时间被限制在离散时间网格中。然而，Hansel[4]表明，将峰值强加到电网上可能会严重扭曲某些网络的同步动态。积分误差仅随计算步长线性减小，因此一个非常小的h对于准确地捕捉动力学是必要的。另一种解决方案是在网格点之间插值膜电位，并在连续时间内评估传入的尖峰对神经元网格的影响[4,5]。该概念在[6]中得到扩展，将其与亚阈值动力学的精确集成相结合(参见[7])。在这里，我们讨论第10.2.2节中描述的方案如何包含离网尖峰时间

如果最小传播延迟大于或等于计算步长h，并且使用适当的时间表示，则可以很容易地将连续尖峰时间合并到离散时间模拟中，而不必实现中央排队结构。在10.2.2节讨论的网络中，首先将亚阈值动态从t推进到t + h一个时间步，然后应用尖峰准则。如果神经元状态通过标准(例如,通过一个膜电位高于阈值),神经元发出分配一个高峰的时间t + h。现在,让我们假设实际上升时间可以确定更准确地说,通过插值的膜电位或反相动力学或任何其他方法,这样t < tspike≤t + h。如果传播延迟神经元的突触后的目标是k·h,事件应该在tspike + k·h时间变得可见，这是在更新间隔(t + k·h,t + (k + 1)·h)内。因此，峰值时间的适当表示由整数时间戳t + h和浮点偏移量δ = tspike−t组成。根据定义，δ在区间(0,h)内。这种表示法的选择使得第10.2.2节中描述的基础结构只需要进行最小的更改。传播延迟k仍然可以用于将事件排序到将在步骤(t + k·h,t + (k + 1)·h)中读取的段中，但是环缓冲区适合于在每个段中保存事件向量，而不是单个值。事件的权值w和偏移量δ被附加到向量上。当神经元执行这个更新步骤时，向量首先按照δ递增的顺序排序。请注意，向量只是最简单的实现，可以用更复杂的数据结构(如日历队列)代替。[8]

然后将阈下动态从时间步的开始推进到第一个事件的到达时间，此时神经元状态被修改以考虑第一个事件。然后在第一个事件的到达时间和第二个事件的到达时间之间推进动态，此时神经元状态被修改以考虑第二个事件，以此类推，直到该更新步骤的所有事件都被处理完。最后将动态从最终事件的到达时间推进到时间步长结束。因此，所有传入的事件都按照正确的时间顺序进行了处理。

上面描述的方案非常通用，可以应用于任何类型的亚阈值动态，允许在离散时间算法内处理和生成连续时间的尖峰。不需要全局事件排队，因为每个神经元都在本地对其事件进行排队。在亚阈值动态是线性的情况下，可以利用这种情况，甚至不是局部的排队是必须的。这涉及到一个稍微复杂的接收尖峰机制，参见[6]。

4 Distributed Networks

神经网络模拟可以消耗大量的内存，特别是在假设生物学上真实的连接水平时。在皮层中，每个神经元大约有104个传入突触，其局部区域的连接概率约为0.1[9]。因此，满足这两个约束的网络必须至少有105个神经元。这相当于大约1毫米3的皮质组织，并且代表了模拟的阈值网络大小，因为超过这个点，突触的数量只随着神经元的数量线性增加，而不是像较小的系统那样呈二次增长。这样的网络包含109个突触，即使使用极其简单的突触表示，也需要几gb的RAM。这种情况自然引起了人们对分布式计算的极大兴趣，例如[3,10,11]。然而，分布提出了在模拟系统中维持因果关系的新问题。如果神经元预投射到神经元post的延迟为k·h，则无论两个神经元是否位于同一台机器上，神经元预在t时刻产生的峰值在t + k·h时刻都应该被神经元post看到。

在[3]中，证明了将突触放置在突触后神经元的机器上比放置在突触前神经元的机器上更有效地分布神经元模拟。这相当于分布一个神经元的轴突，但保持其树突的局部。这样，当一个神经元激活时，只有它的索引必须通过计算机网络发送，而不是每个突触后目标的权重和延迟。对于具有生物学上现实的连接水平的神经网络，这可以代表信息交流量的几个数量级的差异。确保峰值总是按时传递的一种方法是在每个时间步中进行通信，在所有神经元被更新之后，但在它们的缓冲区的读取位置被增加之前(参见第2节)。10.2.2)。然而，就通信效率而言，这种方法不是最优的。机器之间的通信有开销，因此发送一条N字节的消息比发送N条各1字节的消息更有效。幸运的是，通常可以减少通信频率，但仍然可以正确地交付事件。为此，有必要确定模拟系统中神经元之间的最小传播延迟，dmin = kmin·h。与第10.2.2节中描述的dmax一样，根据实现，dmin可以在创建神经元网络之前指定，也可以在神经元连接时动态确定。根据定义，峰值不能在产生后的kmin时间步之前对突触后神经元产生影响。因此，只要保持峰值的时间顺序，就可以以kmin时间步长的间隔进行通信。这可能是一个显著的改进，因为最小延迟可能比计算时间步长大得多。

保持峰值的时间顺序有两个部分:通信前的正确存储和通信后的正确传递。如果峰值被限制在离散时间网格中，为了正确存储，每台机器将峰值神经元的索引存储在缓冲区中就足够了，用标记将在一个时间步骤中峰值的神经元的索引与在前一步或下一步中峰值的神经元的索引分开。因此，在kmin时间步长结束时，缓冲区包含kmin块神经元索引，以kmin−1令牌分隔。然后，机器将这个索引缓冲区发送给所有其他机器，并依次接收缓冲区。如10.3节所述，如果尖峰不受网格的约束，那么除了尖峰神经元的索引外，其尖峰偏移量δ也必须被缓冲和传递。为了正确传递，有必要在考虑时间顺序的同时激活这些缓冲中记录的神经元的突触。索引在缓冲区中的位置表示传递神经元触发的信息的通信延迟klag，即第一个数据块中的索引klag = kmin，第二个数据块中的索引klag = kmin - 1，以此类推，直到最后一个数据块中的索引klag = 1。注意，这是假设在交换尖峰数据之前，所有环缓冲区的读位置都增加了(参见第10.2.2节)。如果交换了顺序，那么通信延迟的范围从第一个块的kmin−1到最后一个块的1。如果从突触中编码的传播延迟中减去通信延迟，那么该事件将在与串行模拟完全相同的时间被突触后神经元看到。例如，考虑一个从神经元前到神经元后的突触，其权重为w，延迟为k·h。在串行模拟中，如果神经元在时间t预发射一个尖峰，w将沿着当前读取位置添加到第k段的环缓冲区中。在分布式模拟中，w将沿着当前读取位置添加到神经元post的环缓冲区k - klag段，其中klag由神经元pre的索引在接收索引缓冲区中的位置决定。[3]中讨论了这种方法的一个稍微复杂的版本。

5 Conclusions and Perspectives

我们已经展示了如何使用相对简单的方法和数据结构来模拟离散时间内的尖峰神经元网络，同时可靠地维持事件的时间顺序。如果将峰值时间约束在离散时间网格中，则该框架适用于无传播延迟的网络，也适用于任意延迟为计算步长h的整数倍的网络。如果不将峰值时间约束在网格中，则该框架仅适用于传播延迟大于等于计算步长h的网络延迟必须是h的整数倍这一点可以放宽，因为浮点偏移量和延迟总是可以动态地重新组合以产生整数延迟和浮点偏移量。所有这些网络都可以以对称的方式在分布式环境中实现，即体系结构是对等的，而不是主从的。

这些网络可以有效地模拟，因为模拟系统中事件的传递时间已经与突触后神经元的到达时间和模拟的时间分辨率解耦。这是环形缓冲区和通信最小延迟间隔的基础概念。然而，如果传递和到达时间解耦，这对于依赖于突触后神经元状态的突触过程来说可能是有问题的，例如，spike- time -dependent plasticity12,13。如果假设传播延迟主要是树突延迟[14]，则已经开发出一种算法来维持正确的关系。然而，如果传播延迟主要是轴突的，那么这里提出的框架是不够的，必须进行调整。