[Dijkstra]--通路中最大边

最新推荐文章于 2024-05-09 20:53:09 发布

原创最新推荐文章于 2024-05-09 20:53:09 发布 · 245 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

46 篇文章

订阅专栏

本文介绍如何使用修改后的Dijkstra算法解决从点1到点n的最大载重路径问题，通过调整松弛条件来寻找单源单路径下最大流量的路径。

题目来源：poj 1797

题目大意：有一张无向图，n（1<=n<=1000）个顶点，m条边，没有重边。每条边都有载重限制，求从点1到点n的一条路径，使得载重最大，输出该重量。

解题思路：

首先要注意这道题和网络流最大流问题的区别，初学者可能会有点晕：网络流可以由多条路径流到汇点，但这道题只有一条路径！单源，单路径，那么就用Dijkstra算法啦，只不过需要改变下松弛条件：以前是选取X集合外的距离最小的点加入X集合；现在是选取X集合外流量最大的点加入X集合，假设现在选取点u加入X集合，更新点v时——
$d [v] = m a x (d [v], m i n (d [u], g [u] [v]))$ 。意思是首先比较到点u的流量和g[u][v]，选择小的一个作为从u到v的流量，然后再与原来的d[v]比较，选取大的作为新的d[v]。另外要注意的是，改变了松弛条件，相应的，d数组的初始化也要相应的改变，d[s]也要初始化为Inf，而不是0，即初始在起点是有无限大的流量。

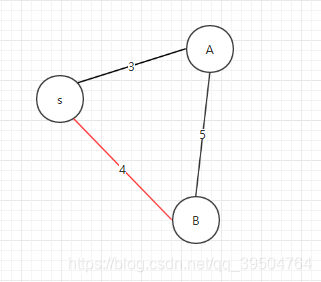
在这里插入图片描述
例：如图所示：从s开始，比较s-A和s-B中载重量更大的哪个，选中B。再比较以B为中介是否可以使s-A的载重量变大，先取 $m i n (d [B], G [B] [A])$ 即 $m i n (4, 5) = 4$ ，再取 $m a x (3, 4) = 4$ ，故以B为中介可以使s-A的载重量变大。

参考：参考

#include <iostream>
#include <vector>
using namespace std;
const int maxn = 1010;
const int INF = 0x3ffffff;
int G[maxn][maxn];
bool vis[maxn] = {false};
int dis[maxn]; //从1点到该位置的最大承载量
int N, M;

int Dijkstra()
{
    fill(vis, vis + maxn, false);
    fill(dis, dis + maxn, 0);
    dis[1] = INF;                //初始化注意！
    for (int i = 1; i <= N; i++) //循环n次
    {
        int u = -1; //使d[u]最小且还没有被访问的结点
        int max = 0;
        for (int j = 1; j <= N; j++)
        {
            if (vis[j] == false && dis[j] > max)
            {
                u = j;
                max = dis[j];
            }
        }
        if (u == -1)
        {
            break;
        }
        vis[u] = true;
        for (int i = 1; i <= N; i++)
        {
            if (vis[i] == false && G[u][i] != INF && dis[i] < min(dis[u], G[u][i])) //改变松弛条件
            {
                dis[i] = min(dis[u], G[u][i]);
            }
        }
    }
    return dis[N];
}

int main()
{
    int T;
    cin >> T;
    int index = 1;
    while (T--)
    {
        cin >> N >> M;
        fill(G[0], G[0] + maxn * maxn, INF);
        int u, v, w;
        for (int i = 1; i <= M; i++)
        {
            scanf("%d %d %d", &u, &v, &w);
            G[u][v] = G[v][u] = w;
        }
        cout << "Scenario #" << index++ << ":" << endl;
        cout << Dijkstra() << endl
             << endl;
    }
    return 0;
}