Mesh网格：教你如何画个球（没UV）

第二篇博文，不整那些大路货，来整个球

对于网格来说，需要的计算每个顶点的位置，面片的链接方式，然后UV的分布，最后是法线。

最难的是UV，本篇的球体也没有写出UV的写法（效果有点差）。

这是我想了两三天的写法，其实实现得并不好，但是好在比较动态，Shader中计算光照的时候能用得上这个代码，就能看到逐顶点和片元的时候比较好的效果。

原理很简单，我们假设一个球体的横向割面和纵向割面一致，那么，就能从公式得到球体的各个点的坐标。

因为首先在一个圆上的某一点，我们知道圆心和半径，再加上我一个圆的切割次数就可以得出它的坐标，即（Center.x+R*cosA，Center.y+R*sinA）。

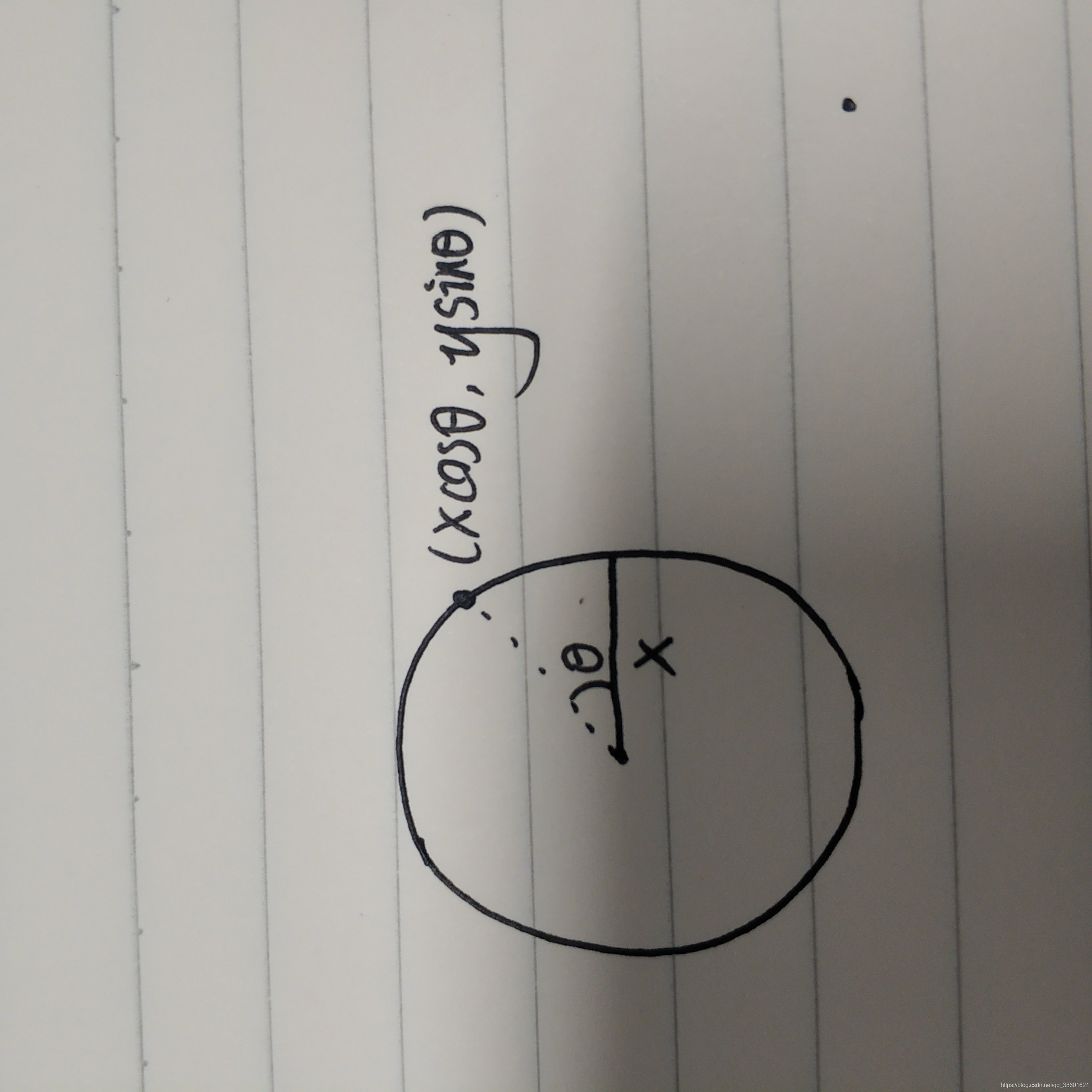
那么，如果我们的圆切割切割X遍，那么我们在高度上会有(X/2+1)个小圆，它们的半径也可以根据我们的公式得出，如图：

然后法线就可以很简单的根据顶点坐标-圆心坐标得出~。

下面就是我们的代码了：

 

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

[ExecuteInEditMode]
[RequireComponent(typeof(MeshFilter),typeof(MeshRenderer))]
public class MeshSphere : MonoBehaviour
{
    [Header("球心")]
    private Vector3 SphereCenter;
    [Header("细节分段")]
    public int segMent;
    [Header("球体半径")]
    public float Radius;
    private Vector3[] SphereFrame;
    private Vector3[][] vertices;
    private Vector3[] verticesCenter;
    private float[] verticesRadius;
    Vector3[] verticesFinal;
    private int heightSegMent;
    private Mesh SphereMesh;
    private Vector2[] UV;
    private void Update()
    {
        SphereCenter = this.transform.position;
        StartCoroutine(DrawSphere());
    }
    IEnumerator DrawSphere()
    {
        SphereMesh = new Mesh();

        //
        SphereFrame = new Vector3[segMent * 4];
        float SegMentAngle = Mathf.Deg2Rad * 360 / segMent;
        //Debug.Log("切片角度是" + SegMentAngle);
        //Debug.Log(Mathf.Sin(0));


        float inCurrentAngel = 0;
        WaitForSeconds wait = new WaitForSeconds(0.01f);
        for (int i = 0; i < segMent; i++) 
        {//xy圆写法
            float cosA = Mathf.Cos(inCurrentAngel);
            float sinA = Mathf.Sin(inCurrentAngel);
            SphereFrame[i] = new Vector3(cosA * Radius + SphereCenter.x, sinA * Radius + SphereCenter.y);
            inCurrentAngel += SegMentAngle;
        }
        for (int i = segMent; i < segMent*2; i++)
        {//xz圆写法
            float cosA = Mathf.Cos(inCurrentAngel);
            float sinA = Mathf.Sin(inCurrentAngel);
            SphereFrame[i] = new Vector3(cosA * Radius + SphereCenter.x, 0, sinA * Radius + SphereCenter.z);
            inCurrentAngel += SegMentAngle;
        }
        //划定圆的坐标
        heightSegMent = segMent / 2 + 1;
        vertices = new Vector3[heightSegMent][];//顶点数组
        verticesCenter = new Vector3[heightSegMent];//每层圆心数组
        verticesRadius = new float[heightSegMent];//每层半径数组

        float CurrentAngle = 90 * Mathf.PI / 180;
        for (int i = 0; i < heightSegMent; i++) 
        {//计算高度和每个高度时的圆心和半径
            float sinA = Mathf.Sin(CurrentAngle);
            float cosA = Mathf.Cos(CurrentAngle);
            vertices[i] = new Vector3[segMent];
            verticesCenter[i] = new Vector3(SphereCenter.x, sinA * Radius + SphereCenter.y, SphereCenter.z);
            verticesRadius[i] = cosA * Radius;
            //Debug.Log("当前分段" + i + "高度是" + verticesCenter[i] + "此时的sin角度是" + sinA);
            CurrentAngle += SegMentAngle;
        }

        float DrawAngle = 0;
        for (int u = 0; u < heightSegMent; u++)
        {//给圆赋上其顶点
            for (int i = 0; i < segMent; i++) 
            {
                float cosA = Mathf.Cos(DrawAngle);
                float sinA = Mathf.Sin(DrawAngle);
                vertices[u][i] = new Vector3(cosA * verticesRadius[u] + verticesCenter[u].x, verticesCenter[u].y, sinA * verticesRadius[u] + verticesCenter[u].z);
                DrawAngle += SegMentAngle;
                //yield return wait;
            }
        }
        //Debug.Log("当前高度分段" + verticesCenter.Length);
        verticesFinal = new Vector3[heightSegMent * segMent];
        for (int i = 0; i < heightSegMent; i++) 
        {//将二维数组赋给最终的总顶点数组
            vertices[i].CopyTo(verticesFinal, i * segMent);
        }
        SphereMesh.vertices = verticesFinal;

        Vector3[] SphereNor = new Vector3[verticesFinal.Length];
        for (int i = 0; i < verticesFinal.Length;i++)
        {
            SphereNor[i] = verticesFinal[i] - SphereCenter;
        }
        int[] triganles = new int[heightSegMent * segMent * 6];
        for (int u = 0, v = segMent - 1, w = 0, x = 1; u < heightSegMent - 1; u++, x++, v += segMent, w += segMent) 
        {//U代表层数，v代表当前开启层数的下一层的末尾点序号,w代表当前层数的初始序号,
            for (int i = u*segMent*6, j = w; i < x*segMent * 6 - 6; i += 6, j++) 
            {//如果是每层分四段，那么一层就是24个点去组三角形
                triganles[i + 1] = j + segMent;//4
                triganles[i] = triganles[i + 1] + 1;
                triganles[i + 2] = j;
                triganles[i + 3] = triganles[i + 2] + 1;
                triganles[i + 4] = triganles[i];
                triganles[i + 5] = triganles[i + 2];
            }
            triganles[x * segMent * 6 - 4] = v;
            triganles[x * segMent * 6 - 5] = v + segMent;
            triganles[x * segMent * 6 - 6] = triganles[x * segMent * 6 - 4] + 1;
            triganles[x * segMent * 6 - 3] = w;
            triganles[x * segMent * 6 - 2] = triganles[x * segMent * 6 - 6];
            triganles[x * segMent * 6 - 1] = v;
        }
        SphereMesh.triangles = triganles;
        SphereMesh.normals = SphereNor;

        SphereMesh.name = "画球";
        this.GetComponent<MeshFilter>().mesh = SphereMesh;
        yield return wait;
    }
}

这样就实现了一个任意割面的球体，这个球体的片面细节完全是我们自己定义的。这种方法实际上比较low，因为会造成面片的损耗比较大，越靠近两极的面片数量越密集，这对于游戏的内存来说是不利的。

效果图：第一个是割面25次的。第二次割面有200多次。第三次割面只有四次。

这种经纬线的球形画法Unity已经没有了，

目前是用八面体来扩张成的球形，而且UV方面也比较方便。

放个大神的链接：https://catlikecoding.com/unity/tutorials/cube-sphere/