Burg法求解AR(p)模型参数（三）Levinson递推公式

第一章 Levinson递推公式

第一节 概念

        如果 Γ_n+1 正定，对1≤k≤n有

其中

第二节 最佳线性预测

        设 {X_t}是零均值平稳序列。考虑用X₁，X₂，……X_n对 X_n+1进行线性预测。也就是用X₁，X₂，……X_n的线性组合对 X_n+1进行预测

        如果 a_n 是 n阶Yule-Walker系数，则对任何线性预测b_n^TX_n ，利用
                                                               
                                                               
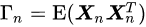
        得到

式(4)表明，在均方误差意义下， a_n^TX_n是 X_n+1 的最佳线性预测。

第三节 AR（p）序列的判定

        由自协方差函数判断一个平稳序列是否是 AR（p）序列。

        如果实数γ_k（k=0,1，……n） ，使得

正定，则Yule-Walker系数a_n满足最小相位条件：

如果 Γ_n正定，称a_n,n为 {X_t} 或 {γ_k}的 n阶偏相关系数。由 AR（p）序列的性质可以知道，AR（p）序列的Yule-Walker系数是

即 AR（p）序列的偏相关系数是p后截尾的。 零均值平稳序列{X_t} 是 AR（p） 序列的充分必要条件是，它的偏相关系数a_n,n 在 p后截尾。