I - Moon Game FZU - 2148 （叉积，凸四边形）

最新推荐文章于 2018-07-25 20:34:09 发布

你的你的都是你的

最新推荐文章于 2018-07-25 20:34:09 发布

阅读量337

点赞数

CC 4.0 BY-SA版权

分类专栏： FZU 数学 vj

本文链接：https://blog.youkuaiyun.com/qq_38158040/article/details/77108392

vj 同时被 3 个专栏收录

20 篇文章

订阅专栏

数学

10 篇文章

订阅专栏

FZU

0 篇文章

订阅专栏

本文介绍了一种计算平面上若干个点可以组成多少个凸四边形的方法。通过计算三角形面积来判断第四个点是否位于由前三点构成的三角形之外，从而确定这些点能否构成凸四边形。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：点击打开链接

题目大意：给你若干个点，找出能形成多少个凸四边形；

题解：

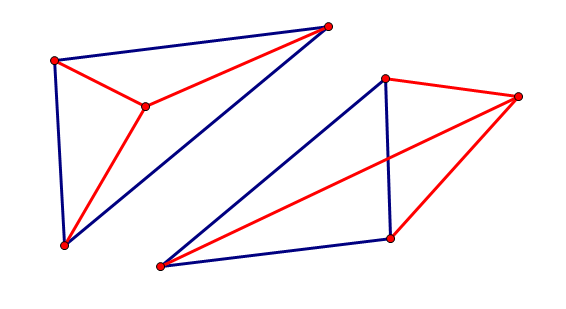
凸四边形中三个定点形成一个三角形 S ，第四个点必在这个三角形外，所以用第四个点与其他三个点相连，会形成三个三角形，如果这三个三角形的面积和与三角形 S 的面积相等则不是凸四边形；

如下图：

#include <iostream>
#include <string>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <iomanip>
#include <map>
using namespace std;
typedef long long ll;

struct point{
  int x,y;
}point[50];
int area(int x1,int y1,int x2,int y2,int x3,int y3)
{
    return abs((x2-x1)*(y3-y1)-(y2-y1)*(x3-x1));
}
int solve(int i,int j,int k,int l)
{
    int Area[4];
    Area[0]=area(point[i].x,point[i].y,point[j].x,point[j].y,point[k].x,point[k].y);
    Area[1]=area(point[i].x,point[i].y,point[j].x,point[j].y,point[l].x,point[l].y);
    Area[2]=area(point[i].x,point[i].y,point[k].x,point[k].y,point[l].x,point[l].y);
    Area[3]=area(point[j].x,point[j].y,point[k].x,point[k].y,point[l].x,point[l].y);
    sort(Area,Area+4);
    if(Area[3]!=Area[0]+Area[1]+Area[2]) return 1;
    else return 0;
}

int main()
{
    int T; cin>>T;
    int kase=0;
    while(T--){
        int n; cin>>n;
        for(int i=0;i<n;i++){
            cin>>point[i].x>>point[i].y;
        }
        int num=0;
        for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
        for(int k=j+1;k<n;k++)
        for(int l=k+1;l<n;l++){
            if(solve(i,j,k,l))
                num++;
        }
        cout<<"Case "<<++kase<<": "<<num<<endl;


    }
    return 0;
}