1123 Is It a Complete AVL Tree (30分)

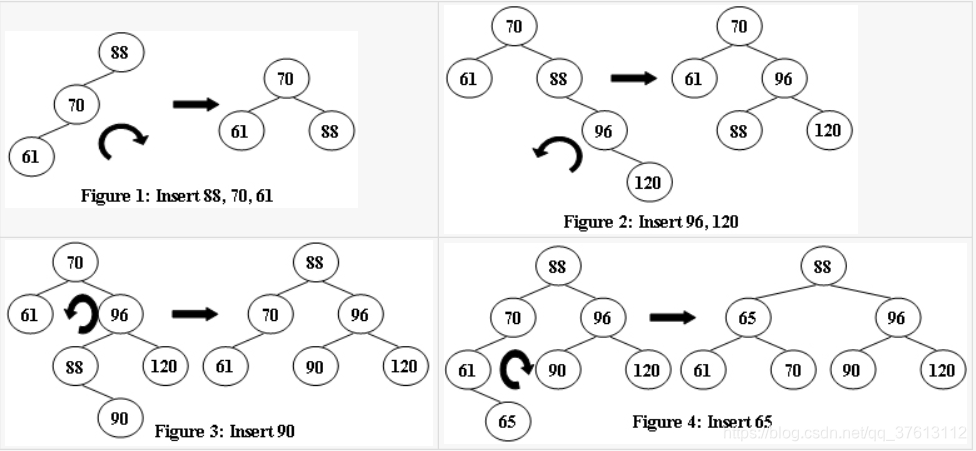
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
typedef struct node {
	int data, depth = 1;
	node* l = NULL, * r = NULL;
}*tree;

int n;

int getDepth(tree t) {
	if (t == NULL)return 0;
	else
		return getDepth(t->r) > getDepth(t->l) ? getDepth(t->r) + 1 : getDepth(t->l) + 1;
}

int getDegree(tree t) {
	return getDepth(t->l) - getDepth(t->r);
}

void R(tree &t) {
	tree temp = t->l;
	t->l = temp->r;
	temp->r = t;
	temp->depth = getDepth(temp);
	t->depth = getDepth(t);
	t = temp;
}

void L(tree& t) {
	tree temp = t->r;
	t->r = temp->l;
	temp->l = t;
	temp->depth = getDepth(temp);
	t->depth = getDepth(t);
	t = temp;
}

void insert(tree& t,int data) {
	if (t == NULL) {
		t = new node();
		t->data = data;
		return;
	}
	if (data < t->data) {
		insert(t->l, data);
		if (getDegree(t) == 2) {
			if (getDegree(t->l) == 1) {
				R(t);
			}
			else if (getDegree(t->l) == -1) {
				L(t->l);
				R(t);
			}
		}
	}
	else {
		insert(t->r, data);
		if (getDegree(t) == -2) {
			if (getDegree(t->r) == -1) {
				L(t);
			}
			else if (getDegree(t->r) == 1) {
				R(t->r);
				L(t);
			}
		}
	}
}

void level(tree t,bool &isCBT) {
	queue<tree>q;
	q.push(t);
	int i = 0;
	bool flag = false;
	while (!q.empty()) {
		tree temp = q.front();
		q.pop();
		if (temp != NULL) {
			if (i != n - 1)cout << temp->data << " ";
			else
				cout << temp->data << endl;
			i++;
			if (flag)isCBT = false;
			q.push(temp->l);
			q.push(temp->r);
		}
		else
			flag = true;
	}
}
int main() {
	cin >> n;
	tree t = NULL;
	for (int i = 0; i < n; i++) {
		int d;
		cin >> d;
		insert(t, d);
	}
	bool isCBT = true;
	level(t, isCBT);
	if (isCBT)cout << "YES" << endl;
	else
		cout << "NO" << endl;
	return 0;
}