卡尔曼滤波在处理信号的噪声方面及其有用,最近看到一篇博客,讲解的通俗易懂,就不重复阐述了。附上个地址:卡尔曼滤波,通俗易懂
import matplotlib.pyplot as plt
import numpy as np
#创建噪声
NUM = 300
np.random.seed(4)
Noise= np.random.randn(NUM) #高斯分布随机噪声
Noise_std = np.random.randn(NUM) #测量噪声
X = [0]*NUM
Y = [0]*NUM
#创建数据集
for i in range(1,NUM):
X[i] = np.sin(0.2*i)
Noise_std_ = np.square(np.var(Noise_std)) #求方差
Noise_ = np.square(np.var(Noise))
P = [0]* NUM #每次的最优偏差
K = [0]* NUM #卡尔曼增益
S = X + Noise_std #测量值
for i in range(1,NUM):
P[i] = np.square(P[i-1]) + 0.1*Noise_
K[i] = 0.1*np.sqrt( P[i]/( Noise_std_ + P[i]))
Y[i] = Y[i-1] + K[i] * (S[i] - Y[i-1])
P[i] = np.sqrt((1-K[i])*P[i])
print(P[i])
plt.plot(X,color = 'r',label = '数据集')
plt.plot(S,color = 'g',label = '数据测量获取值(带噪声)')
plt.plot(Y,color = 'b',label = '过滤后的数据')
plt.show()
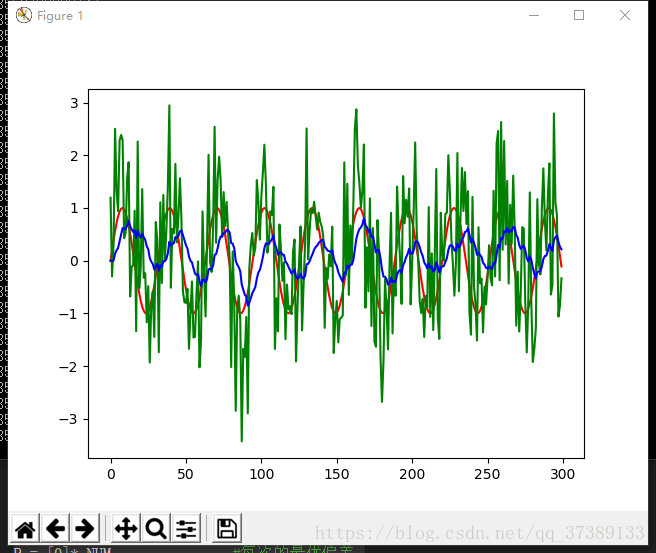
一般的对于我们嵌入式来说,在处理陀螺仪数据上面比较经典,有很多陀螺仪虽然都是自带卡尔曼滤波处理,但是仍然值得学习尝试处理。
#include "math.h"
//在稳定情况下采集陀螺仪数据
//测定其噪声的均值
float getNoiseGyro() {
short i = 20;
float temp = 0;
for (; i > 0;i--) {
temp+=GetXW(); //获取单个轴的角速度
}
temp /= i;
return temp;
}
float XW[5] = {0};
short count = 0;
float P = 0;
float Noise = 0; //Noise = getNoiseGyro()
float XA_ = 0;
float getGyroSW() { //获取的是滤波后的角速度
short i = 0;
float temp = 0;
float P1,K;
count++;
count %= 5;
XW[count] = GetXW(); //跟新添加
for (; i < 5;i++) { //求取本状态的稳定值,预测量
temp += XW[i];
}
temp /= 5;
P1 = P * P + 0.002; //0.002为角速度的阈值误差
K = 0.1*P1 / (P1 + pow(Noise,2) ); //计算增益
XA_ = XA_ + K * (temp - XA_);
P = sqrt((1-K) * P1 ); //跟新偏差
return XA_;
}以上就是一个简单尝试。








 本文通过Python实现卡尔曼滤波,有效去除信号噪声,特别适用于嵌入式系统中陀螺仪数据处理,展示了从创建数据集、添加噪声到应用滤波的全过程。
本文通过Python实现卡尔曼滤波,有效去除信号噪声,特别适用于嵌入式系统中陀螺仪数据处理,展示了从创建数据集、添加噪声到应用滤波的全过程。
















 1559
1559

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








