LeetCode（5）—— 最长回文子串

题目内容

描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例：

• 示例1

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

• 示例2

输入: "cbbd"
输出: "bb"

解法1 —— 暴力法

我觉得这应该是最开始的想法吧，简单粗暴，两个指针把所有可能的子串都定出来，然后写个判断是否是回文的函数。缺点就是时间复杂度高咯，两重循环$O(n^2)$，再来个判断又是$O(n)$，总起来$O(n^3)$，空间复杂度$O(n)$。代码还是给一下。

 def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        maxPalindromeLen = 0
        maxPalindrome = ""

        n = len(s)
        if n == 1:
            maxPalindromeLen = 1
            maxPalindrome = s
            return maxPalindrome

        for i in range(n):
            for j in range(i, n):
                sub_str=s[i:j+1]
                if self.isPalindrome(sub_str):
                    if j - i + 1 > maxPalindromeLen:
                        maxPalindromeLen = j - i + 1
                        maxPalindrome = sub_str
        return maxPalindrome

    def isPalindrome(self, s):
        n = len(s)
        # 根据回文的对称性，两个指针往中间靠拢
        head = 0
        tail = n - 1
        while (head <= tail):
            if s[head] != s[tail]:
                return False
            head += 1
            tail -= 1

        return True

解法2 —— 动态规划

If “aba” is a palindrome, is “xabax” and palindrome? Similarly is “xabay” a palindrome?

这个思路稍微想一下也能想到。既然aba是回文，那xabay怎么判断呢？这个时候动态规划就派上用场了，我们定义：

$$p(i,j)=\begin{cases} 1,\quad s_i s_{i+1}...s_j是回文 \\ 0, \quad s_i s_{i+1}...s_j不是回文\end{cases}$$
$$显然p(i,i)=1 ,即单个字符自身一定是回文$$

动态转移方程如下：

$$p(i,j)=p(i+1,j-1)==1并且(s[i]==s[j])$$
$$p(i,i+1)=(s[i]==s[i+1])$$

再说一下，动态规划的那张表其实只要填一半，填表的顺序如下图所示

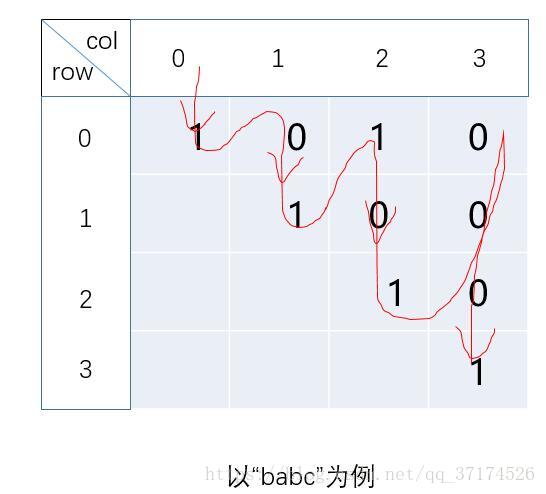
最后找出p[row][col]==1，并且|row-col|最大的那个子串就ok。

    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """


        n=len(s)
        if n==0:
            return  ""

        maxPalindromeLen = 1
        maxPalindrome = s[0]
        array=[[False for i in range(n)] for i in range(n) ]
        for i in range(n):
            array[i][i]=True
        for col in range(n):
            for row in range(0,col):
                if col-row==1:
                    array[row][col]=(s[row]==s[col])
                else:
                    array[row][col] = array[row+1][col-1]&(s[row] == s[col])

                if(array[row][col] and (col-row+1>maxPalindromeLen)):
                    maxPalindromeLen = col-row+1
                    maxPalindrome =s[row:col+1]
        return maxPalindrome

不过还是时间超限了。时间复杂度$O(n^2)$,空间复杂度$O(n^2)$。

解法3 —— 中心枚举法

该解法代码参考自：https://blog.youkuaiyun.com/asd136912/article/details/78987624。

根据自己的理解修改了代码，主要思路和动态规划扩展的向左右思路一致，要分奇数和偶数分别寻找，AC。
delta就是试探过程中回文的半径

    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        n=len(s)
        if n==0:
            return  ""
        maxPalindromeLen = 1
        maxPalindrome = s[0]
        for i in range(n):
            # 子串长度为奇数时
            delta=1
            while(i-delta>=0 and i+delta<n):
                if s[i-delta]==s[i+delta]:
                    # 下一次试探的试探长度加1
                    delta+=1
                else:
                    break
            # 试探长度减1，delta就是当前i为中心点，左右扩展的长度
            delta-=1
            if 2*delta+1>maxPalindromeLen:
                maxPalindromeLen=2*delta+1
                maxPalindrome=s[i-delta:i+delta+1]

            # 子串长度为偶数时,将s[i]和s[i+1]视为绑定
            # 分别向s[i]的左边和s[i+1]的右边试探
            # 最开始delta要初始化为0，因为需要比较s[i]和s[i+1]
            delta=0
            if (i+1<n):
                while(i-delta>=0 and i+1+delta<n):
                    if s[i-delta]==s[i+1+delta]:
                        delta+=1
                    else:
                        break
            delta-=1
            if 2*delta+2>maxPalindromeLen:
                maxPalindromeLen=2*delta+2
                maxPalindrome=s[i-delta:i+1+delta+1]

        return maxPalindrome

解法4 —— Manacher算法

算法详细介绍 https://articles.leetcode.com/longest-palindromic-substring-part-ii/

时间复杂度$O(n)$ ,空间复杂度$O(n)$

    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        n = len(s)
        if n == 0:
            return ""

        # 根据Manacher算法预处理原字符串的方法添加字符
        T="#"+"#".join(s)+"#"
        # print(T)

        n_T=len(T)
        p=[0 for i in range(n_T)]
        # 中心点，最右边的边界
        C,R=0,0
        for i in range(1,n_T-1):
            # 关于中心的对称点
            i_mirro=2*C-i
            if i<R:
                p[i]=min(p[i_mirro],R-i)
            # 其实这条语句可以不用写，因为在创建的时候就初始化为0了
            else:
                p[i]=0
            # 继续向左右延伸试探（以i为中心的回文）
            while(i+1+p[i]<n_T and i-1-p[i]>=0 and T[i+1+p[i]]==T[i-1-p[i]] ):
                p[i]+=1
            # 调整C和R的位置
            if(i+p[i]>R):
                C=i
                R=i+p[i]

        # 找P数组里面最大的数
        maxPalindromeLen = 0
        centerIndex=0
        for i in range(1, n_T - 1):
            if p[i]>maxPalindromeLen:
                maxPalindromeLen=p[i]
                centerIndex=i
        # 把"#"去掉
        return T[centerIndex-maxPalindromeLen:centerIndex+maxPalindromeLen+1].replace("#","")

要注意的地方

• python截取字符串，

  从下标begin到下标end截取时，str[begin:end+1]

• join函数和replace函数的使用

• 二维“数组”的创建（实质上是嵌套的List）