UPFT：使用前缀微调节省95%的训练开销？AI Lab新作

论文标题：

The First Few Tokens Are All You Need: An Efficient and Effective Unsupervised Prefix Fine-Tuning Method for Reasoning Models

论文地址：

https://arxiv.org/pdf/2503.0287

动机

使用大模型做推理任务（数学）时，多次采样并观察CoT输出，发现输出的前缀部分（问题理解和初步规划）具有较高的一致性与准确性，不同采样结果的差异，以及开始出错的步骤都发生在中后部分

观察到上述现象后，希望在“前缀”上做文章，提高大模型自我迭代的效果（利用新数据集继续优化一个reasoning模型

方法论

提出UPFT方法（Unsupervised Prefix Fine-Tuning）：

1. 在新数据集上采样一批推理推理数据，只取其中的前缀部分（前缀长度是超参数）。使用以下提示词
   

2. 为了保留模型正常回答问题的能力，避免灾难遗忘，以一定概率采样一批完整的推理数据；注意这里不去做结果正确与否的校验

3. 使用上述数据做SFT训练（实际上是自监督）

论文花费了一定篇幅做公式推导，提出了覆盖度和准确性两个概念，进而确定了工作方向：

1. 提高覆盖度：需要让模型推理结果的开头部分通用性更强，即涵盖各种解决思路
2. 保持准确性：生成推理结果的开头部分，要能推导出正确答案

关于1:
如前文所述，大模型做推理任务时，越靠前时推理部分越相似，如果后续有很多训练数据只是包含了前缀部分，那么训练集的“覆盖度”本身就比较高
关于2: 没有什么额外操作，由于训练数据由相同的初始模型产生，不同采样结果的正确率在实验组和对照组之间都是一样的

实验结果

无监督实验

SFT对照组：多次采样初始模型，生成完整的问答对，不做正确性校验

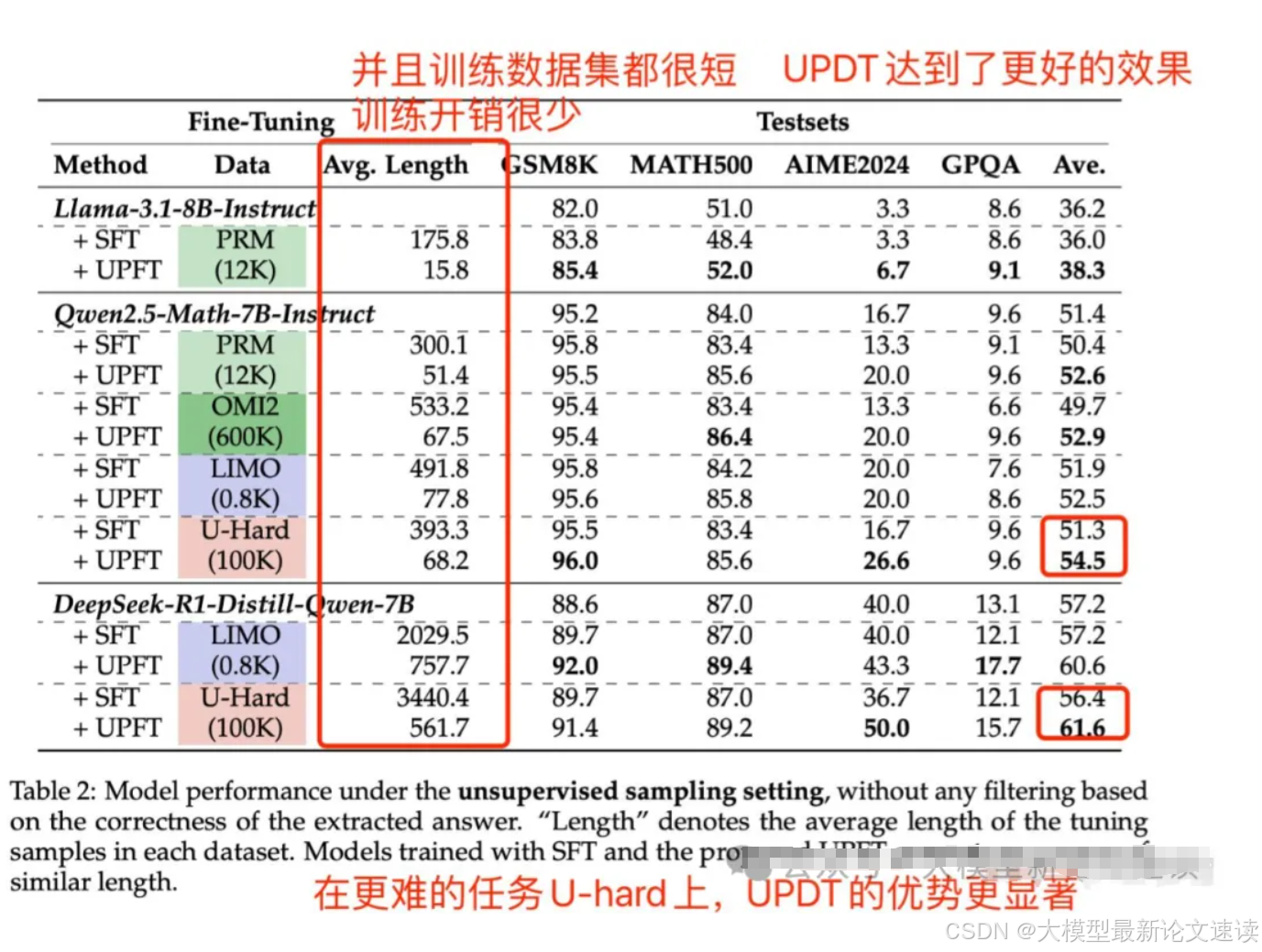
这里的结论比较符合直觉：未经校验的合成数据可能包含很多噪声，“无监督”的SFT方法效果与zero-shot结果持平或更低

有监督实验

RFT对照组：多次采样初始模型，去掉最终结果不正确的部分，生成完整的问答对

+Lable Filter实验组：UPFT基础上，对数据集正确性做校验，确保采样的数据能推导正确结果

单纯的UPFT，效果逼近于有监督的RFT方法

UPFT可以很方便地加上正确性校验，转换成有监督的训练方法，此时效果最好

总结

此工作提出了一种新的大模型自迭代方法，使训练开销急剧下降，同时也保持了与有监督微调方法持平的准确性

如果我们有一批新的问题集，可考虑使用此方法快速进行迭代优化，并且无需标注数据；从实验结果来看，即使有条件打标注，此方法的准确性也更好；

但此工作的有些实验结论还很反直觉，方法论推导部分也只是使用数学语言梳理了动机和优化方向，并不能solid地推导出前缀学习的优越性，实验分数差距也没有很大。此外测试数据都是思考路径较短的数学题，方法可迁移性存疑；

总之还需要进一步探索和验证