PowerAttention: 更准确高效的静态稀疏注意力

论文标题：
PowerAttention: Exponentially Scaling of Receptive Fields for Effective Sparse Attention

论文地址：
https://arxiv.org/pdf/2503.0287

一、动机

Self-attention的O(N^2)复杂度极大地拖累了模型性能，稀疏注意力机制通过减少token之间的交互来改进计算效率。稀疏注意力可分为动态和静态两种类型，前者会动态地挑选更合适的key来与query交互，后者则遵循固定的挑选模式。目前的实践中，一般采用动静结合的方式，例如deepseek的Native Sparse Attention

作者认为当前的静态稀疏注意力模式，要么存在信息遗漏，要么不能快速地扩展上下文“视野”，希望找到一个更加完整、高效的静态稀疏注意力模式

二、相关工作及缺陷

1. Sliding Window Attention 滑动窗口

覆盖度

每个token可与窗口范围内的token直接交互，与其他token间接交互

视野扩张

随着窗口线性扩张，假设目标token与当前token的距离是N，需要堆叠的attention层数为：
$$N/window\_size=O(N)$$

2. Stride Slash Attention 跨步注意力

Stride Slash Attention原文是一篇CV工作，它选择了两类token来与当前query交互（如下图所示），二维的图像拉平成长度为N的序列，可知行模式和列模式所选择token的数量都是√N

此篇论文中展示的Stride Slash Attention略有不同：行模式是一个常数长度的window，而非原文中的√N长度

覆盖度

由于行模式的存在，和上述滑动窗口一样，每个token能够与所有token相关联，不会遗漏信息

视野扩张

当前token首先找到距离目标token最近的列模式token，然后访问与此token交互的最远的行模式token，最终找到目标token，需要堆叠的attention层数为：

$$1+\surd N/(2\ast window\_size)=O(\surd N)$$

解释：
首次到达列模式距离目标最近的token需要一层attention；由于列模式每次向前跨越√N步，所以此时与目标token的距离为不会再超过√N（否则列模式便可以继续向前跨步），平均为√N/2；此后每层attention最多能扩展window_size步，还需要√N / (2*window_size)层attention

3. Dilated Attention 膨胀注意力

类似于膨胀CNN，感受野留出空洞从而扩大视野范围

覆盖度

每次以固定间隔挑选交互的token，留下的空洞永远无法与当前token建立联系

视野扩张

和滑动窗口一样，虽然通过留出空洞扩大了单层视野范围，但依然是线性扩张速度，找到目标token需要的attention层数为：
$$N/dilated\_window\_size=O(N)$$
其中dilated_window_size = windows_size / dilated_rate

4. LongNet

LongNet在多个窗口范围内应用膨胀注意力，并且窗口大小与膨胀率成等比例关系

覆盖度

如上图所示，存在访问不到的token，损失了信息

视野扩张

膨胀率不断倍增，视野范围以指数函数增长，所以到达目标token需要logN层attention模块

三、本文方法

提出PowerAttention：以2^k（k=0~logN）为间隔选择需要交互的token

覆盖度

如上图所示，每个位置的token都能建立关系

视野扩张

间隔范围以指数形式扩张，到达目标token需要logN层attention

分析

按照以上attention的邻接矩阵视角，在每层选择关联token数量相等的情况下，蓝色方块的数量以指数函数增长，所以我们为了更有效地扩展视野范围，需要在每层预留出指数增长的“空白”，让蓝色方块更均匀地填充进去，牺牲近距离的直接关系，来置换更多远距离的间接关系；

这里其实忽视了远、近距离依赖的重要性差异，也忽视了直接、间接依赖的重要性差异

四、实验结果

1. 困惑度

所有方法在4k~32k上下文上都保持了较低的困惑度，只有LongNet和Dilated在32k上下文效果微差

2. 大海捞针实验

不外推（测试数据长度不超过训练数据长度）
PowerAttention方法最接近于Full Attention的效果

外推（测试数据长度超过训练数据长度）

Sliding Window和LongNet方法在上下文长度超过8k后效果便急剧下降，这里就不再拿它们做外推实验；Dilated在所有上下文尺度上表现都不好，也不做后续外推实验

3. 长文本基准测试

在RULER基准上进行测试，它包含13个长上下文任务。PowerAttention在每个上下文尺度上的平均分都最好

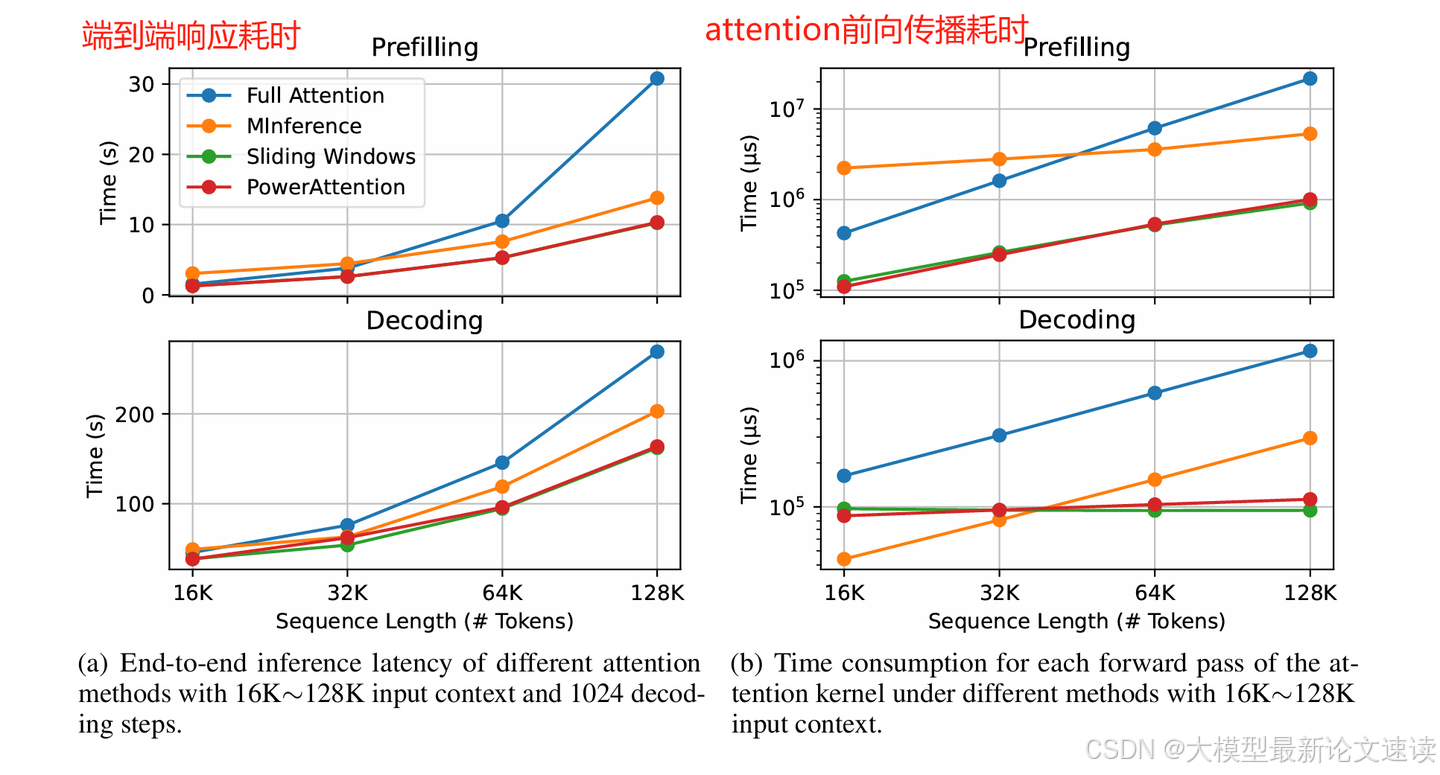
4. 性能测试

PowerAttention的性能与滑动窗口attention相当

5. 视野范围可视化

为了验证各稀疏attention方案的视野扩张，与理论分析是否一致，作者设计了以下实验：

• 在一个固定位置设置passkey，passkey是一个单词，有6种可能的取值（苹果、葡萄等）
• 把每一层的attention结果切分成block
• 训练一个简单的逻辑回归分类器，输入不同位置block的attention向量，预测passkey（六分类任务）
• 统计每一层、每一个位置的attention向量，输入到上述分类器后预测passkey的准确率

实验结果如下：

解释：

• 每张图一开始有一根纯白的柱子，表示此位置放置了passkey线索
• 在Full Attention中，浅层的attention结果便可准确预测出passkey，说明模型一开始便与之建立了关系，和理论分析一致
• 在Sliding Window中，浅层的attention只有在距离很近时才能预测passkey，表明视野受限，然后随着layer的加深，视野范围线性扩张，和理论分析一致。堆叠到28层时，最远位置的准确率只有48%
• 在PowerAttention中（未经继续预训练和微调），浅层的attention间隔着能准确预测并且间隔呈指数阔大；随着layer的加深，深色间隔越来越少，这样的现象与理论分析一致。最终到28层时，最远位置的准确为56%
• 如果PowerAttention经过了继续与训练和微调，那么最后在此任务上能达到100%的准确率

五、总结

此工作提出了一种新的大模型静态稀疏注意力模式，实现简单，实验结果证明了其有效性。此方法本质上是让交互token的选择更平均，牺牲了部分近距离直接交互，换取了更多远距离间接交互，从实验结果和视野范围可视化来看，这样的置换是划算的