2D离散傅里叶变换及逆变换的matlab实现

积分线性变换可以将信号或图像在更适合的域内表达，并且使得解决相关问题更容易，在图像分析中最常用的积分显示变换是傅里叶变换、离散余弦变换与小波变换。

1d傅里叶变换由傅里叶(Fourier)提出，1d傅里叶变换将函数f(x)变换到频率域F(t)表达。F称作频谱，可以显示不同频率的相对成分。用i(根号下-1)表示虚数单位，1d连续傅里叶变换表达为：

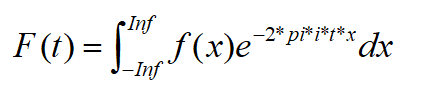
逆变换为

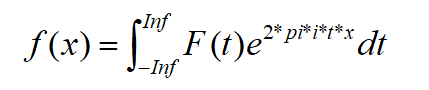
相应地，对于下标从0开始的离散变量f(x)，1d离散傅里叶变换和逆变换分别为：

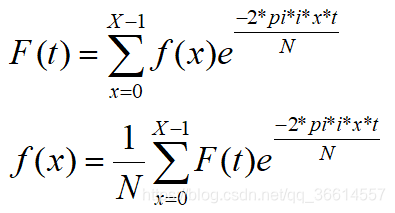
离散傅里叶变换(DFT)的时间复杂度为O(n2)，使用快速傅里叶变换(FFT)会降低为 O(nlogn)

从1d傅里叶变换可容易推广到2d，对于连续空间f，2d连续傅里叶变换和逆变换如下：