多传感器融合中的观测信号表示

最新推荐文章于 2025-05-20 16:56:02 发布

doubleslow;

最新推荐文章于 2025-05-20 16:56:02 发布

阅读量1.4k

点赞数 3

CC 4.0 BY-SA版权

分类专栏：数据融合文章标签：数据融合多传感器数据融合

本文链接：https://blog.youkuaiyun.com/qq_36607894/article/details/90899714

现在在研究多传感器数据融合这个领域，大补一下基础理论。本文大量涉及通信原理，信号与系统，信号检测与估计，概率和随机过程的先修知识，由于避免不了遗忘，复习过程极其痛苦······，特此梳理清晰，以飨后来者。

要进行数据融合，得有数据，数据就是观测信号，一般是离散时间序列。

而实际中的观测信号由于信道中的各种干扰（如电阻和传输介质中电子的随机运动产生的热噪声，宇宙噪声，电子不均匀发射引起的散弹噪声等），一定都有各种畸变，我们要做的是：首先提取出失真的观测信号中的有用信息，然后根据一定的算法将多方信息进行融合，以便于做出更准确的判断，指导，决策。

信号的分类多种多样，比如连续离散，周期非周期，能量信号和功率信号···如果根据信号中参量的特性分类则：

信号中所有参量都已知，信号只是时间的函数，则称为确知信号。
若有参量未知，则称为参量信号。
若有参量随机，则称为随机参量信号。实际中，我们主要接触的就是这类信号，其振幅，相位，到达时间可能都是随机的。比如：随机振幅信号，随机频率信号，随机相位信号，随机到达时间信号（TDOA不同）。 也可能多个参数都随机。

(TDOA:Time Delay of Arrival，到达时间延迟)

下面介绍随机参量信号和随机噪声，通信系统接收信号的具体数学表示。

1. 随机振幅信号

既然振幅是随机的，那么就符合一定的统计特性。通常，比较符合实际的统计特性假设是瑞利分布（Rayleigh Distribution）：
$aσa2e−a22σa2,a≥00,otherwisep(a)=\left\{ \begin{aligned} &\frac{a}{\sigma_a^2}e^{-\frac{a^2}{2\sigma_a^2}}&,&a\geq0\\ &0&,&otherwise \end{aligned} \right. \tag1$
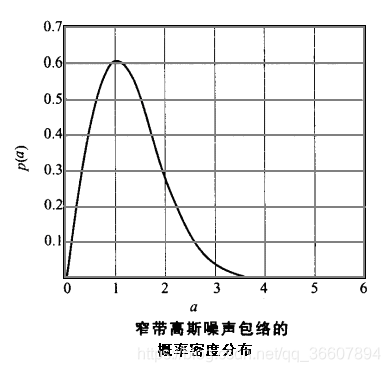
在这里插入图片描述
此图仅供看个概貌。。。

两个正交高斯噪声信号之和的包络服从瑞利分布。
而两个正交高斯噪声信号之和一定是窄带高斯噪声，所以窄带高斯噪声的包络是服从瑞利分布的。而包络就是振幅呀，所以通信接收信号的振幅服从瑞利分布。
通信发送和接受的信号都是窄带信号。因为热噪声（是白噪声）和解调后的信号在接收机里会被滤波，所以一定是带限的。
因此论文和研究中动不动就假设接收噪声是白噪声实际上带来的误差可能会很大，因为根本不符实际，但信道中的噪声假设为白噪声是可以的。
此外，一定要记住，通信系统中的接收机噪声，主要来源于接收机内部的热噪声，就是各种电子元件里的电子随机运动产生的扰动电压，并不是从信道里跑进来的！！这是很多人包括以前的我理解的误区。
一般认为不同信道的噪声统计特性正交，而无线通信的多径分量经过损耗和衰减，信噪比极低，信号被淹没，可以认为是统计特性正交的窄带高斯噪声，所以多径分量通常被认为是服从瑞利分布的。
如果再叠加上主信号则就服从莱斯分布了，后文详述。
$E(A)=∫−∞∞ap(a)da=∫0∞a2σa2e−a22σa2da=∫0∞−ade−a22σa2E(A)=\int_{-\infty}^\infty ap(a)da=\int_{0}^\infty\frac{a^2}{\sigma_a^2}e^{-\frac{a^2}{2\sigma_a^2}}da=\int_{0}^\infty -ade^{-\frac{a^2}{2\sigma_a^2}}$
$=−ae−a22σa2∣0∞+∫0∞e−a22σa2da=0+2σa∫0∞e−(a2σa)2da2σa=π2σa=-ae^{-\frac{a^2}{2\sigma_a^2}}|_0^{\infty}+\int_{0}^\infty e^{-\frac{a^2}{2\sigma_a^2}}da=0+\sqrt2\sigma_a\int_{0}^\infty e^{-(\frac{a}{\sqrt2\sigma_a})^2}d\frac{a}{\sqrt2\sigma_a}=\sqrt{\frac \pi2}\sigma_a$
$≈1.2533σa\approx1.2533\sigma_a$