本文深入探讨了凸优化中的近似方法，包括近似操作、近似梯度方法及其加速策略。详细介绍了近似梯度的更新规则、线搜索策略以及Douglas-Rachford Splitting算法在非光滑、光滑+非光滑和非光滑+非光滑最小化问题中的应用。此外，还讨论了固定点属性和反射操作在优化过程中的作用。
文章目录
近似方法
1. 近似操作
凸函数 h h h的近似操作也称为近似映射(proximal mapping)定义为 p r o x h ( x ) = arg min u ( h ( u ) + 1 2 ∥ u − x ∥ 2 2 ) prox_h(x)=\argmin\limits_{u}\left(h(u)+\frac{1}{2}\|u-x\|^2_2\right) proxh(x)=uargmin(h(u)+21∥u−x∥22)。
下面是一些函数的例子：
1. 对于 h ( x ) = 0 h(x)=0 h(x)=0，其 p r o x h ( x ) = x prox_h(x)=x proxh(x)=x;
2. 对于指示函数( X → { 0 , 1 } X\rightarrow\{0,1\} X→{
0,1}） h ( x ) h(x) h(x)，在凸集 X X X上，有 p r o x h ( x ) = arg min u ∈ X ∥ u − x ∥ 2 2 = π X ( x ) prox_h(x)=\argmin_{u\in X}\|u-x\|^2_2=\pi_X(x) proxh(x)=u∈Xargmin∥u−x∥22=πX(x);
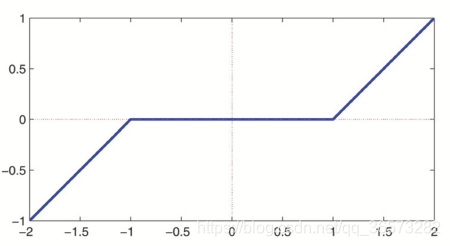
3. 对于 h ( x ) = ∥ x ∥ 1 h(x)=\|x\|_1 h(x)=∥x∥1， p r o x h ( x ) i = { x i − 1 , x i ≥ 1 0 , ∥ x i ∥ x i + 1 , x i ≤ − 1 prox_h(x)_i=\left\{\begin{aligned}&x_i-1,& x_i\geq 1\\ &0, & \|x_i\|\\&x_i+1, &x_i\leq -1\end{aligned}\right. proxh(x)i=⎩⎪⎨⎪⎧xi−1,0,xi+1,xi≥1∥xi∥xi≤−1 该近似映射函数被称为soft-threshold。
2. 近似梯度方法
将无约束的优化问题分成两个部分， m i n { f ( x ) ≜ g ( x ) + h ( x ) } min\left\{f(x)\triangleq g(x)+h(x)\right\} min{
f(x)≜g(x)+h(x)}。其中 g g g是凸的且可微，且 d o m g = R n dom\ g=\mathbb{R}^n dom g=Rn。 h h h是凸的，且代价较小(inexpensive)的近似操作。
近似梯度方法为 x k + 1 = p r o x t k h ( x k − t k ∇ g ( x k ) ) x_{k+1}=prox_{t_kh}(x_k-t_k\nabla g(x_k)) xk+1=proxtkh(xk−tk∇g(xk))。其中 t k > 0 t_k>0 tk>0是步长。
使用近似操作的定义对近似梯度方法进行转换得到 x k + 1 = p r o x t h ( x k − t ∇ g ( x k ) ) = arg min u ( h ( u ) + 1 2 t ∥ u − x k + t ∇ g ( x k ) ∥ 2 2 ) = arg min u ( h ( u ) + g ( x k ) + ∇ g ( x k ) T ( u − x k ) + 1 2 t ∥ u − x k ∥ 2 2 ) x_{k+1}=prox_{th}(x_k-t\nabla g(x_k))\\=\argmin\limits_{u}\left(h(u)+\frac{1}{2t}\|u-x_k+t\nabla g(x_k)\|^2_2\right)\\=\argmin\limits_{u}\left(h(u)+g(x_k)+\nabla g(x_k)^T(u-x_k)+\frac{1}{2t}\|u-x_k\|^2_2\right) xk+1=proxth(xk−t∇g(xk))=uargmin(h(u)+2t1∥u−xk+t∇g(xk)∥22)=uargmin(h(u)+g(xk)+∇g(xk)T(u−xk)+2t1∥u−xk∥22)。
使用前面的例子中的函数举例：
1. 对于 h ( x ) = 0 h(x)=0 h(x)=0，因为 p r o x h ( x ) = x prox_{h}(x)=x proxh(x)=x，所以近似梯度为 x k + 1 = x k − t ∇ g ( x ) x_{k+1}=x_{k}-t\nabla g(x) xk+1=xk−t∇g(x)。
2. 对于 h ( x ) = I X ( x ) h(x)=I_X(x) h(x)=IX(x)，有 x k + 1 = π X ( x k − t ∇ g ( x k ) ) x_{k+1}=\pi_X(x_k-t \nabla g(x_k)) xk+1=πX(xk−t∇g(xk))；
3. 对于 h ( x ) = ∥ x ∥ 1 h(x)=\|x\|_1 h(x)=∥x∥1有 x k + 1 = p r o x t h ( x − t ∇ g ( x ) ) x_{k+1}=prox_{th}(x-t\nabla g(x)) xk+1=proxth(x−t∇g(x))。其中 p r o x t h ( u ) i = { u i − t , u i ≥ t 0 , ∣ u i ∣ ≤ t u i + t , x i ≤ − t prox_{th}(u)_i=\left\{\begin{aligned}&u_i-t, & u_i \geq t\\ & 0, & |u_i|\leq t\\ &u_i+t, &x_i\leq -t\end{aligned}\right. proxth(u)i=⎩⎪⎨⎪⎧ui−t,0,ui+t,ui≥t∣ui∣≤txi≤−t
性质： 如果函数 h h h是凸且闭的，那么 p r o x h ( x ) = arg min u ( h ( u ) + 1 2 ∥ u − x ∥ 2 2 ) prox_h(x)=\argmin\limits_{u}\left(h(u)+\frac{1}{2}\|u-x\|^2_2\right) proxh(x)=uargmin(h(u)+21∥u−x∥22)存在且对所有的 x x x唯一
该性质可以由 h ( u ) + 1 2 ∥ u − x ∥ 2 2 h(u)+\frac{1}{2}\|u-x\|^2_2 h(u)+21∥u−x∥22强凸得到。
性质： u = p r o x h ( x ) u=prox_h(x) u=proxh(x)与下面的等同：
1. x − u ∈ ∂ h ( u ) x-u\in \partial h(u) x−u∈∂h(u);
2. 对于所有的 x x x， h ( z ) ≥ h ( u ) + ( x − u ) T ( z − u ) h(z)\geq h(u)+(x-u)^T(z-u) h(z)≥h(u)+(x−u)T(z−u)
证明：因为 0 ∈ ∂ { h ( u ) + 1 2 ∥ u − x ∥ 2 2 } 0\in \partial \{h(u)+\frac{1}{2}\|u-x\|^2_2\} 0∈∂{ h(u)+21∥u−x∥22}，所以 0 ∈ ∂ h ( u ) + u − x 0\in \partial h(u)+u-x 0∈∂h(u)+u−x。此外，对于 g ∈ ∂ h ( u ) g\in \partial h(u) g∈∂h(u)，有 h ( z ) ≥ h ( u ) + g ( z − u ) h(z)\geq h(u)+g(z-u) h(z)≥h(u)+g(z−u)。
性质：在指示函数 I X I_X IX上的近似映射是在 X X X上的欧几里得投影。
p r o x I X ( x ) = arg min u ∈ X ∥ u − x ∥ 2 2 = π X ( x ) prox_{I_X}(x)=\argmin\limits_{u\in X}\|u-x\|^2_2=\pi_{X}(x) proxIX(x)=u∈Xargmin∥u−x∥22=πX(x)，并且 ( x − u ) T ( z − u ) ≤ 0 , ∀ z ∈ X (x-u)^T(z-u)\leq 0, \forall z\in X (x−u)T(z−u)≤0,∀z∈X
证明：首先，对于所有的 z z z 有 h ( z ) ≥ h ( u ) + ( x − u ) T ( z − u ) h(z)\geq h(u)+(x-u)^T(z-u) h(z)≥h(u)+(x−u)T(z−u)，通过指示函数的定义有 h ( z ) = h ( u ) = 0 h(z)=h(u)=0 h(z)=h(u)=0。
性质（固定点）：设函数 f f f是凸的，有点 x ∗ x_* x∗最小化 f ( x ) f(x) f(x)当且仅当 x ∗ = p r o x f ( x ∗ ) x_*=prox_f(x_*) x∗=proxf(x∗)
证明：首先，如果 x ∗ x_* x∗能够最小化 f ( x ) f(x) f(x)，那么我们有 f ( x ) ≥ f ( x ∗ ) f(x)\geq f(x_*) f(x)≥f(x∗)。因此， f ( x ) + 1 2 ∥ x − x ∗ ∥ 2 2 ≥ f ( x ∗ ) + 1 2 ∥ x ∗ − x ∗ ∥ 2 2 f(x)+\frac{1}{2}\|x-x_*\|_2^2\geq f(x_*)+\frac{1}{2}\|x_*-x_*\|^2_2 f(x)+21∥x−x∗∥22≥f(x∗)+21∥x∗−x∗
最低0.47元/天 解锁文章
扫一扫
673
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
