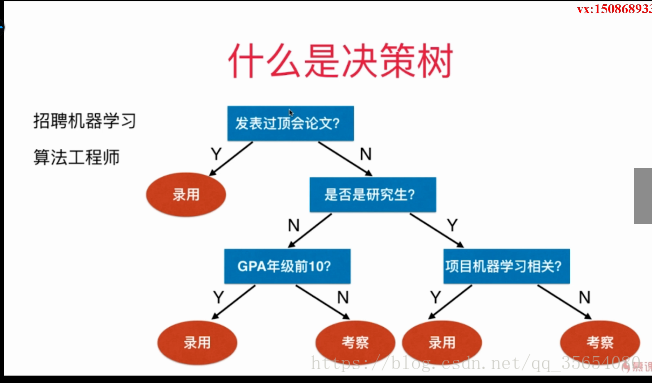
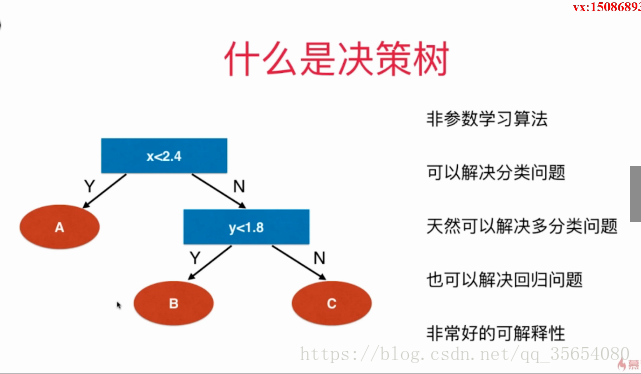
"""决策树"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
iris=datasets.load_iris()
X=iris.data[:,2:]
y=iris.target
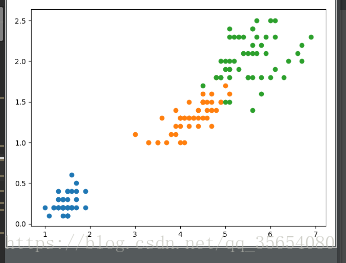
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
dt_clf=DecisionTreeClassifier(max_depth=2,criterion='entropy')
dt_clf.fit(X,y)
def plot_decision_boundary(model,axis):
x0,x1 = np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100))
)
X_new = np.c_[x0.ravel(),x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
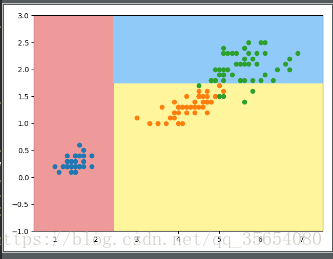
plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)
plot_decision_boundary(dt_clf,axis=[0.5,7.5,-1.0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
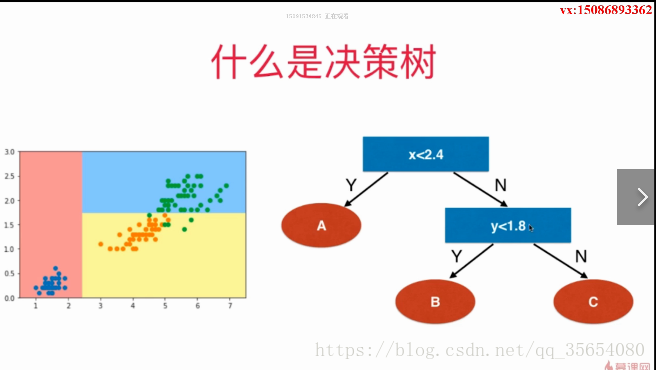








 本文探讨了决策树在解决回归问题时如何利用基尼系数进行特征选择。通过分析,我们发现最佳划分维度是第0维,后续可继续通过第一维进行划分。同时,基尼系数与信息熵在选择最优特征方面表现出相似性。然而,在实际应用中,决策树可能存在过拟合的风险。
本文探讨了决策树在解决回归问题时如何利用基尼系数进行特征选择。通过分析,我们发现最佳划分维度是第0维,后续可继续通过第一维进行划分。同时,基尼系数与信息熵在选择最优特征方面表现出相似性。然而,在实际应用中,决策树可能存在过拟合的风险。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 3937
3937

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








