一、部分题目
2013高教社杯全国大学生数学建模竞赛题目
A题 车道被占用对城市道路通行能力的影响
车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低的现象。由于城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道的通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞。如处理不当,甚至出现区域性拥堵。
车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据。
视频1(附件1)和视频2(附件2)中的两个交通事故处于同一路段的同一横断面,且完全占用两条车道。请研究以下问题:
问题1 根据视频1(附件1),描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力的变化过程。
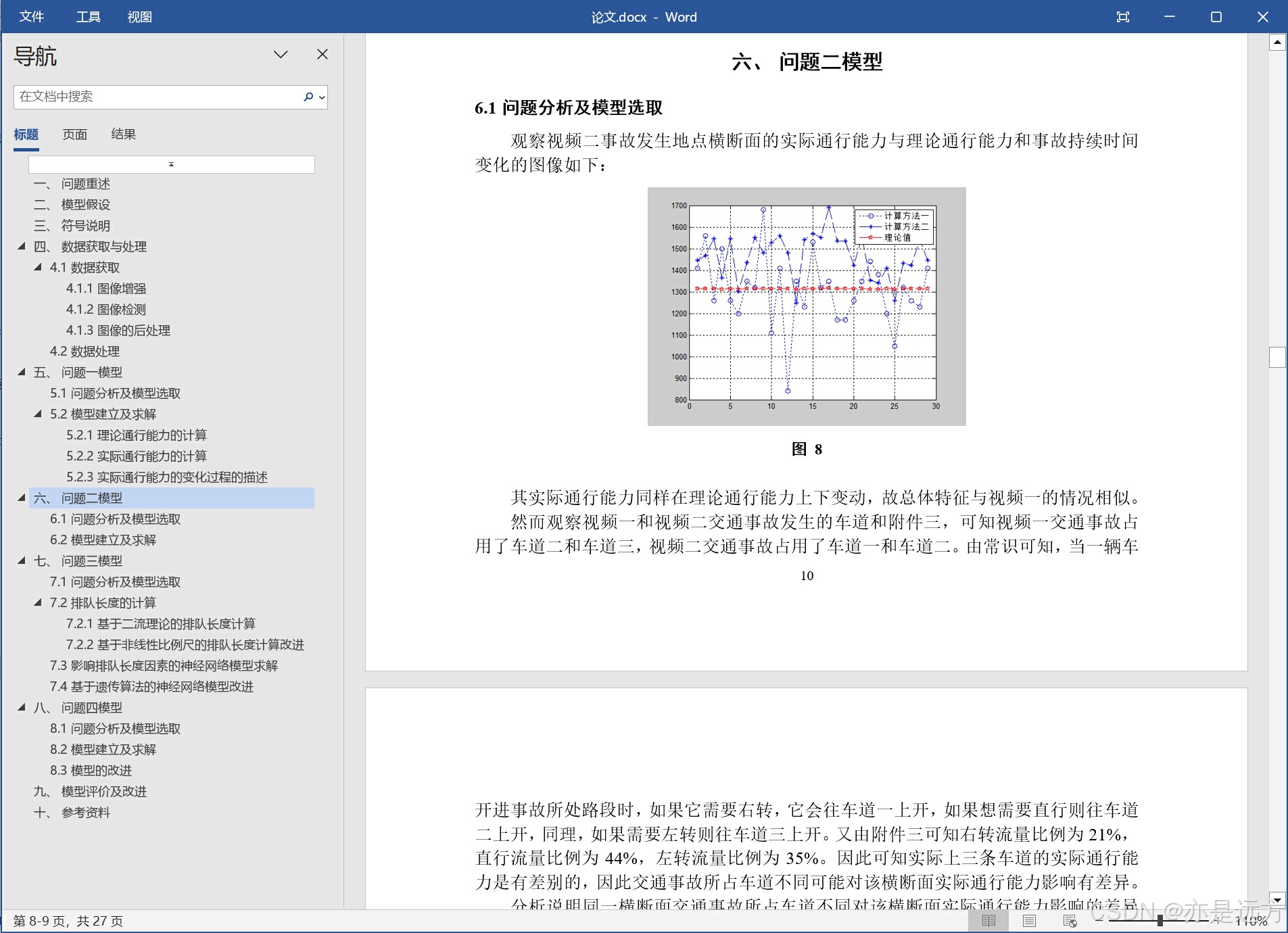
问题2 根据问题1所得结论,结合视频2(附件2),分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异。
问题3 构建数学模型,分析视频1(附件1)中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系。
问题4 假如视频1(附件1)中的交通事故所处横断面距离上游路口变为140米,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离。请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口。
二、部分论文
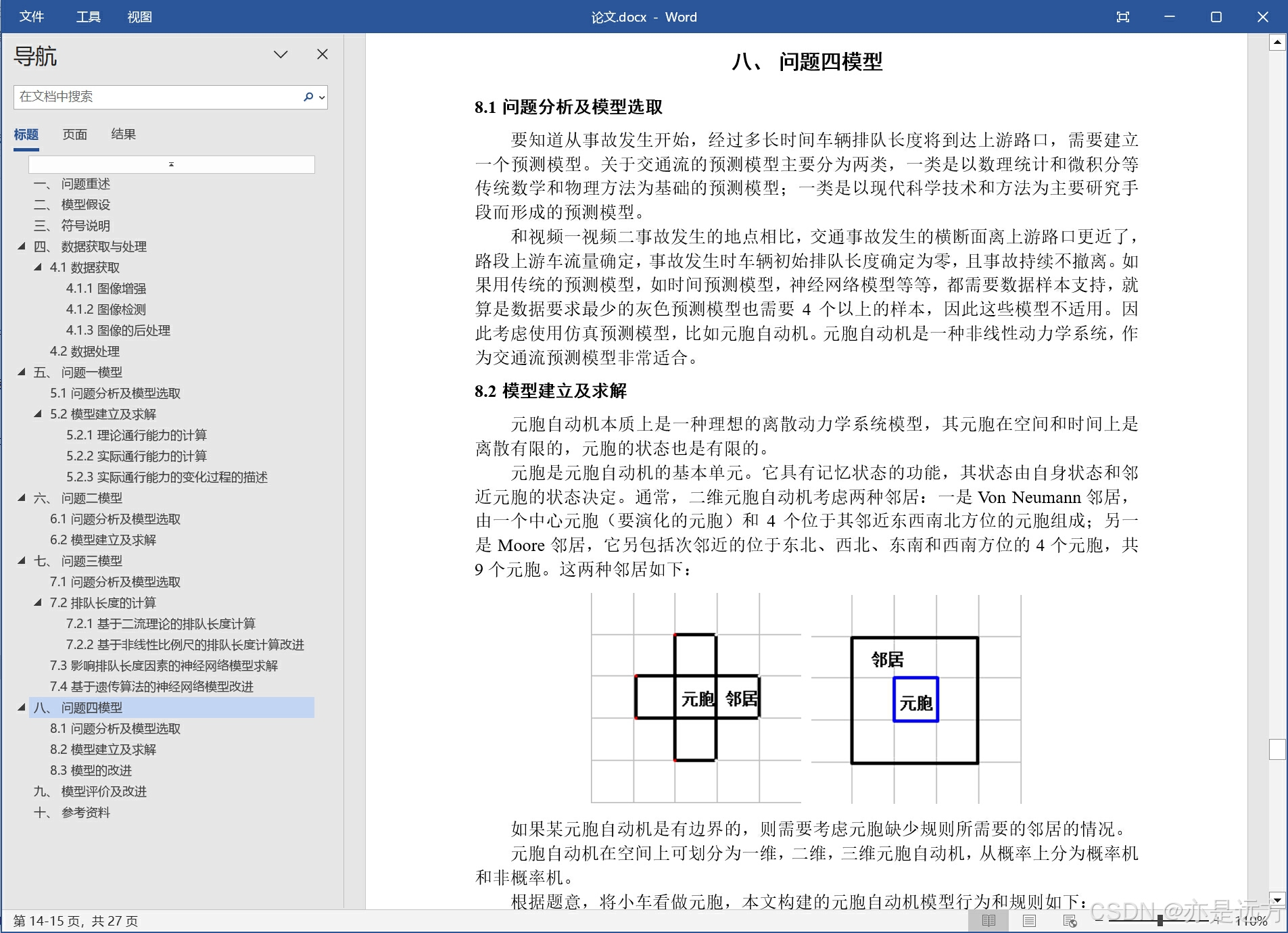
三、部分源代码
问题1
完整代码 https://github.com/yan-fanyu/CUMCM-Paper-And-SourceCode
% 问题1
%% 注意!!! 需要用到视频,请将附件1视频放在当前目录下,并改名为1.mpg’
clear;
close all;
clc;
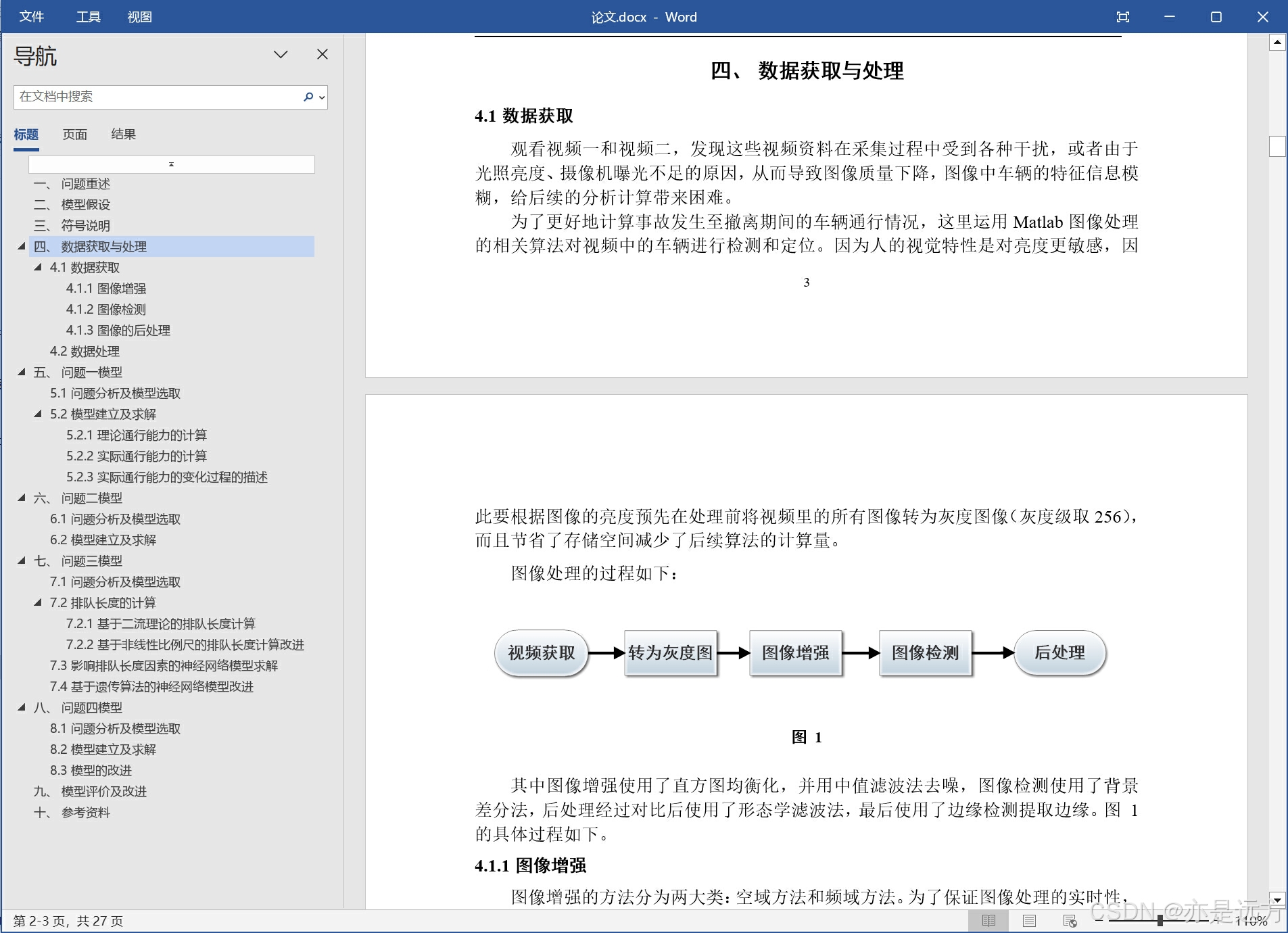
%% 读取视频 且一帧帧的播放
%% 注意!!! 需要用到视频,请将附件1视频放在当前目录下,并改名为1.mpg’
vedio1 = mmreader('1.mpg');
nFrames = vedio1.NumberOfFrames;
vidHeight = vedio1.Height;
vidWidth = vedio1.Width;
%% 选其中的ROI
img = 0;
C1 = read(vedio1,4950);
%imshow(C1);
C1 = rgb2gray(C1);%转为灰度图
C1 =medfilt2( C1,[3,3]); %中值滤波B(1) = read( vedio1, 1 );
K = 0.90;B1 = 0;tmp = zeros(size(C1));M = 30;
for i = 4960:15: nFrames
C = read( vedio1, i );% 大概25帧一秒
tmp = C;
C = rgb2gray(C);%转为灰度图
C = histeq(C); %直方图均衡化
% imshow(C);
% C = retinex(C);
% figure;
C = medfilt2( C,[3,3]); %中值滤波
% imshow(C);
B = K*B1+(1-K)*C1;
D = C-B;
% for j = 2:288-1
% for k = 2:352-1
% if D(j,k)>M && D(j-1,k-1)>M && D(j-1,k)>M && D(j,k-1)>M....
% && D(j+1,k)>M && D(j,k+1)>M && D(j+1,k-1)>M && D(j+1,k+1)>M....
% && D(j-1,k+1)>M
% tmp(j,k) = 255;
% end
% end
% end
D(find(D>M)) = 255;
D(find(D<= M)) = 0;
% level = graythresh(D); %Otsu阈值法
% D = im2bw(D,level);
subplot(1,2,1);
imshow(tmp);
subplot(1,2,2);
%imshow(tmp);
se1=strel('square',2);%圆盘型结构元素
%D = imopen(D,se1);
se=strel('disk',2);%圆盘型结构元素
D=imclose(D,se);%直接闭运算
%D = edge(D,'canny'); %边缘检测
imshow(D);
C1 = C;
B1 = B;
% 从i= 4990开始进行计数
end
问题2
完整代码 https://github.com/yan-fanyu/CUMCM-Paper-And-SourceCode
% 问题2
clear;
close all;
clc;
%%
load('problem2.mat');
che(all(che==0,2),:)=[];che(:,all(che==0,1))=[];
weight = [1 1.5 2];% 权重
for i = 1:size(che,1)
che(i,:) = che(i,:).*weight.*60;
end
x = 1:size(che,1);
plot(x,che(:,1),':o',x,che(:,2),'-*',x,che(:,3),'--o',x,sum(che,2),':*');
grid on;
legend('小型车','中型车','重型车','总和');
%% 计算实际通行能力
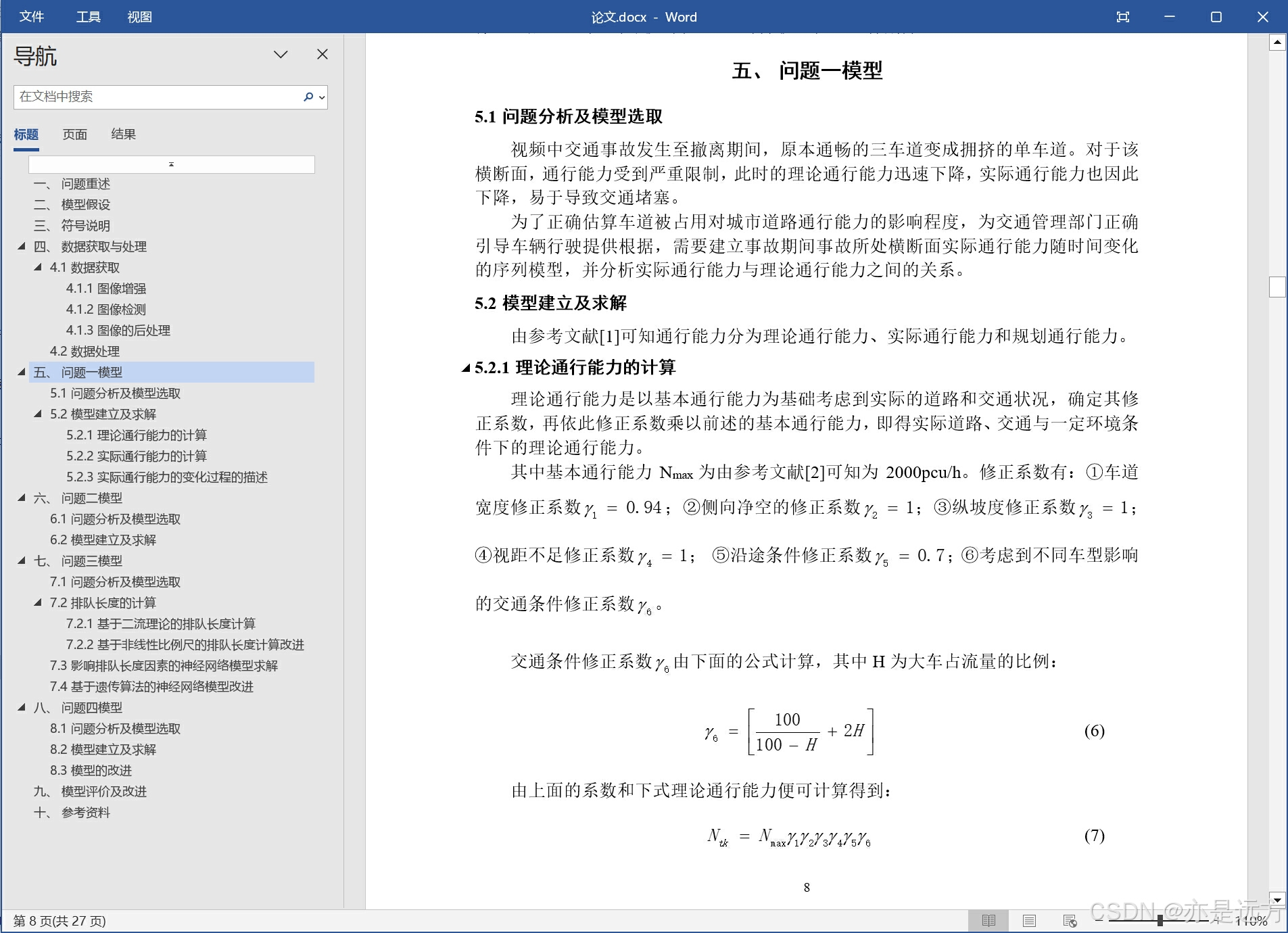
CB = 2000; N = 1; fw = 0.94; fp = 0.9;ehv = 2;
for i = 1:size(che,1)
fhv = 1/(1+(che(i,3)/sum(che(i,:)))*(ehv-1));
Qx(i) = CB*N*fw*fhv*fp;
end
figure;
plot(x,sum(che,2),'b:o');
hold on;
grid on;
plot(x,Qx,'b--*');
%% 可能通行能力计算
CB = 2000;yl = 0.94;yc = 1;yi = 0.7;
for i = 1:size(che,1)
T = che(i,3)/sum(che(i,:));
yt = 100/((100-T)+2*T);
C(i) = CB*yl*yc*yi*yt;
end
plot(x,C,'r--p');
legend('计算方法一','计算方法二','理论值');
%% 上游车流量和通行能力
figure;
plot(x,sum(che,2)./(shangyou*weight'.*60),'o');
grid on;
legend('上游车流量和通行能力');
问题3
完整代码 https://github.com/yan-fanyu/CUMCM-Paper-And-SourceCode
% 问题三
clear;
close all;
clc;
load('problem3.mat');
%% 计算排队长度
M =2;L = 0.120;N0 = 12;
kj = 160;km = 59;
shangyous(1) = shangyou(1);
xiayous(1) = xiayou(1);
%计算累计数
for i = 2:size(shangyou,1)
shangyous(i) = sum(shangyou(1:i,1));
xiayous(i) = sum(xiayou(1:i,1));
end
for i = 2:size(shangyou,1)
D(i) = 1000*(N0+shangyous(i)-xiayous(i)-km*L*M)/(M*(kj-km));
if N0+shangyous(i)-xiayous(i)>= kj*L*M
D(i) = 120;
else
if N0+shangyous(i)-xiayous(i)<= km*L*M
D(i) = 0;
end
end
end
% plot(1:size(shangyou,1),D,':*',1:size(shangyou,1),length,'--o');
% grid on;
% legend('模型计算长度','统计计算的长度');
%% 将时间单独作为一个输入,通行能力和上游车流结合为一个输入(通行能力是成本型)
B = [max(shangyou),min(xiayou)];
W = [min(shangyou),max(xiayou)];
%相对偏差
r(:,1) = abs(shangyou-B(1))./(max(shangyou)-min(shangyou));
r(:,2) = abs(B(2)-xiayou)./(max(xiayou)-min(xiayou));
del(:,1) = abs(shangyou-W(1))./(max(shangyou)-min(shangyou));
del(:,2) = abs(W(2)-xiayou)./(max(xiayou)-min(xiayou));
for i = 1:2
c(i) = (r(:,i)'*del(:,i))./(norm(r(:,i))*norm(del(:,i)));
end
%权重
w(1) = c(1)/sum(c);
w(2) = c(2)/sum(c);
%无量纲化后加权求和
P(:,1) = (shangyou-min(shangyou))./(max(shangyou)-min(shangyou));
P(:,2) = (max(xiayou)-xiayou)./(max(xiayou)-min(xiayou));
score = P*w';
% plot3(score(1:81),time(1:81),length(1:81)','ro');
% grid on;
% xlabel('得分');ylabel('持续时间'):zlabel('排队长度');
%% 神经网络拟合
p=[score(1:81)';time(1:81)']; %输入数据矩阵
t=length(1:81)'; %目标数据矩阵
%利用premnmx函数对数据进行归一化
[pn,PS1]=mapminmax(p); % 对于输入矩阵p和输出矩阵t进行归一化处理
[tn,PS2]=mapminmax(t); % 对于输入矩阵p和输出矩阵t进行归一化处理
dx=[-1,1;-1,1]; %归一化处理后最小值为-1,最大值为1
%BP网络训练
net=newff(dx,[2,5,1],{'tansig','tansig','purelin'},'traingdx'); %建立模型,并用梯度下降法训练.
net.trainParam.show=1000; %1000轮回显示一次结果
net.trainParam.Lr=0.05; %学习速度为0.05
net.trainParam.epochs=50000; %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-2); %均方误差
net=train(net,pn,tn); %开始训练,其中pn,tn分别为输入输出样本
%利用原始数据对BP网络仿真
[m1,m2] = meshgrid(linspace(0.25,0.86,1040),0:1:1039);
test = [reshape(m1,1,size(m1,1)*size(m1,2));reshape(m2,1,size(m2,1)*size(m2,2))];
pn1 = mapminmax('apply',test,PS1);
an=sim(net,pn1); %用训练好的模型进行仿真
a=mapminmax('reverse',an,PS2); % 把仿真得到的数据还原为原始的数量级;
a = reshape(a,size(m1,1),size(m1,2));
a(find(a<0)) = 0;
figure;
mesh(m1,m2,a);
grid on;
xlabel('得分');ylabel('持续时间'):zlabel('排队长度');
问题四
完整代码 https://github.com/yan-fanyu/CUMCM-Paper-And-SourceCode
% 问题4
clear;
close all;
clc;
load('problem4.mat');
disp('程序运行需要较长时间,请稍后。');
for ss = 1:50
%% 元胞自动机进行模拟 1.只区分小车和大车 2. 出现大车相当于同时出现两辆小车 3.车辆匀速
length_car = 4.8;
global length;length = floor(140/length_car);%车道单位长度
global DU TONG; DU = 0; TONG = 255;
% 建道路(255表示畅通,0表示堵塞)
global road ;
road= zeros(5,length); road(2,1) = 255;road(2,:) = 255;road(3,:) = 255;road(4,:) = 255;
road(1,:) = 0;road(5,:) = 0;
road(3,1) = 0;road(4,1) = 0;
flag = zeros(size(road));
imshow(road);
% axis off
% 统计上游车辆不同类型车的比例
shangyou = sum(shangyou1,1)+sum(shangyou2,1);
per_s = shangyou(1)/sum(shangyou);
per_l = shangyou(3)/sum(shangyou);
per_s = per_s/(per_s+per_l);
per_l = 1-per_s;
% 概率方面
weight = [1,2];%车型/当量
shangyou = 1500;%上游车流量
per_newcar = 1500/1800;%每一秒更新的当量数
per_sec = [0.21,0.44,0.35];% 选择车道
v1 = 2;v2 = 1;%道路分为两部分,分别的步进长度(30km/h 1m/s)。
l = 0;%更新的时候选择了大车
% 先要在路段上生成车辆,当量为12
pcu = 12;
while pcu >0
%选择车辆,轮盘赌
if rand<=per_s
pcu = pcu-1;
num = 1;
else
pcu = pcu-2;
num = 2;
end
%生成坐标和车型
while num >0
while road(ceil(rand*3)+1,ceil(rand*length)) == DU end
x = ceil(rand*length);
y = ceil(rand*3);
road(y+1,x) = DU;
num = num-1;
end
end
% 每一秒钟进行车辆更新、车辆前进、车辆换道
t = 0;
while size(find(road(2,:)== 255),2)>2&&size(find(road(2,:)== 255),2)>2&&size(find(road(2,:)== 255),2)>2%三条道没有一条塞满
%前进
for i = 2:4
for j = 2:length
prob = 0.18*j;
if road(i,j) == DU&&flag(i,j) == 0&&rand<prob
if road(i,j-1) == TONG
road(i,j) = TONG;
road(i,j-1) = DU;
flag(i,j) = 1;
if road(2,1) == DU
road(2,1) = TONG;
end
else
%换道
huandao(i,j);
end
end
end
end
%更新车辆
if mod(fix(t/30),2)
if l==1
l = 0;
continue;
end
if rand<=per_newcar
%更新什么车
if rand <=per_s
num = 1;
else
num = 2;
l = 1;
end
%在哪条行车道
while num>0
if rand<=0.44
road(3,length) = DU;
elseif rand<=0.44+0.35
road(4,length) = DU;
else
road(2,length) = DU;
end
num = num-1;
end
end
end
t = t+1;
cal(t) = calline(road);
%imshow(road);
% % % set(gcf,'units','normalized','position',[0,0,1,0.9]);
%pause(0.1);
flag = zeros(size(flag));
end
log(ss) = t;
plot(cal);
grid on;
legend('队长随时间的变化(单位车长)');
end
t = mean(log)/60


























 2787
2787

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










