图文详解AVL树

AVL树(平衡二叉树)

基本介绍

AVL 树是用来维持平衡二叉树的一种解决方案。从上篇二叉搜索树的文章中，总结出二叉搜索树本意是为了优化查找效率，但是在不平衡的极端情况下却会退化成为一个链式结构导致高度变为n从而查找效率变为O(n)。而AVL树会始终保持平衡并且高度为log2(n+1).

它本质上是一颗二叉查找树，基本特征就是左右两个子树的高度差永远不可能大于 1，所以被称为平衡二叉树。

平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1;

AVL树节点类实现

构造用于 AVL 树实现的 Node 类很类似于用于二叉树实现的节点，但是还是有一些显著的差异。AVL 树中的每一个节点都必须包含它自身的高度，所以在类中就会包括一个表示高度的数据成员。而且为了比较存储在节点内的数值，还要有类实现 IComparable 接口。此外，由于节点的高度是如此重要，因而还要包括一个只读的方法来返回节点的高度。 

public class Node : IComparable
{
     public Object element;
     public Node left;
     public Node right;
     public int height;

     public Node(Object data, Node lt, Node rt)
     {
         element = data;
         left = lt;
         right = rt;
         height = 0;
     }

     public Node(Object data)
     {
         element = data;
         left = null;
         right = null;
     }

     public int CompareTo(Object obj)
     {
        return (((int)element).CompareTo((int)obj));
     }

}

 public int GetHeight(Node node)
 {
 if (node== null)
     return -1;
 else
     return node.height;
}

 

AVL树的基本操作

AVL树的操作基本和二叉查找树一样，这里我们关注的是两个变化很大的操作：插入和删除。

AVL树不仅是一颗二叉查找树，它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理，在删除的时候也有可能会破坏树的平衡性，所以我们要做一些特殊的处理，包括：单旋转和双旋转！

插入

插入要分四种情况：

1)右旋---向左子树的左子树中插入新节点(左左插入 LL)

插入1，由于平衡被破坏，我们要对其进行旋转，这时候是右旋，为什么称为右旋呢，其实可以想象以根节点5为中心将其向右旋转，以至于其左边线及左树向上抬起，至左字节3到达上端成为根节点为止：

 

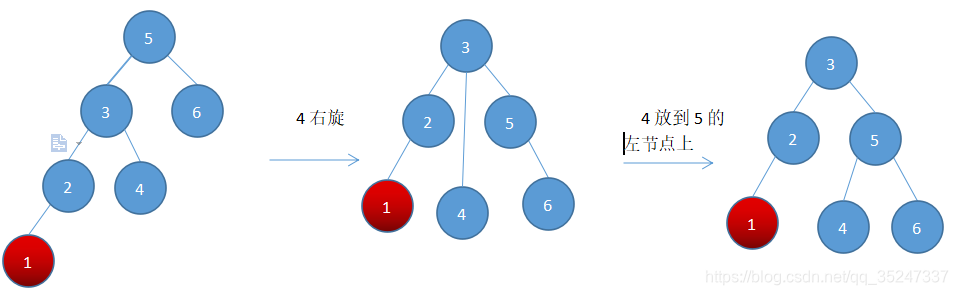
右旋代码：

private Node RightRotate(Node n2)
{
     Node n1 = n2.left;//n2是5 n1是3
     n2.left = n1.right;//节点4调整为节点5的左节点
     n1.right = n2;//3为根节点，5为3的右节点
     //重新设置高度
     n2.height = Math.Max(GetHeight(n2.left), GetHeight(n2.right)) + 1;
     n1.height = Math.Max(GetHeight(n1.left), n2.height) + 1;
     return n1;
}

2)左旋---向右节点的右子树中插入新节点(右右插入 RR)

插入6，由于平衡被破坏，我们要对其进行旋转：

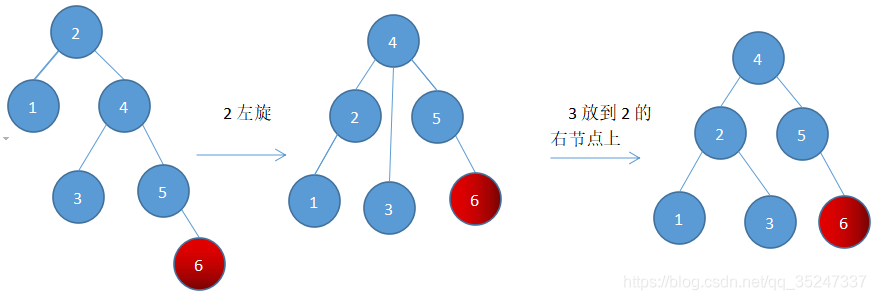
左旋代码：

private Node LeftRotate(Node n1)
{
     Node n2 = n1.right;
     n1.right = n2.left;
     n2.left = n1;
     n1.height = Math.Max(GetHeight(n1.left), GetHeight(n1.right) + 1);
     n2.height = Math.Max(GetHeight(n2.right), n1.height) + 1;
     return n2;
}

3)右左(先右后左)旋---在右节点的左子树插入新节点(右左插入 RL)

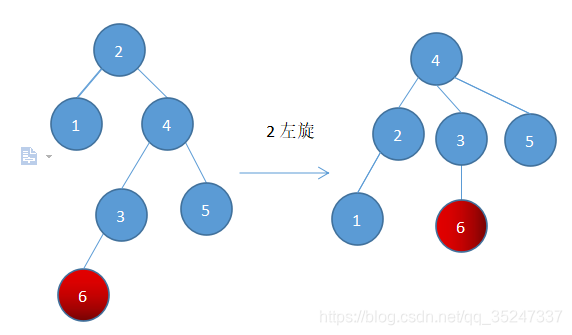
上图可以看到，当插入点在右节点的左子树时(注意，这里节点6不管在节点3的左节点还是右节点都是一样的)，如果单纯的对根节点进行左旋，不管中间的那条叉怎么调整都平衡不了左右子树。所以这时候采用双旋转。

这里的窍门就是先让原本最高高度在树内部的节点调整到边缘来，然后就又可以像前两种情况那样进行单旋转调整了。

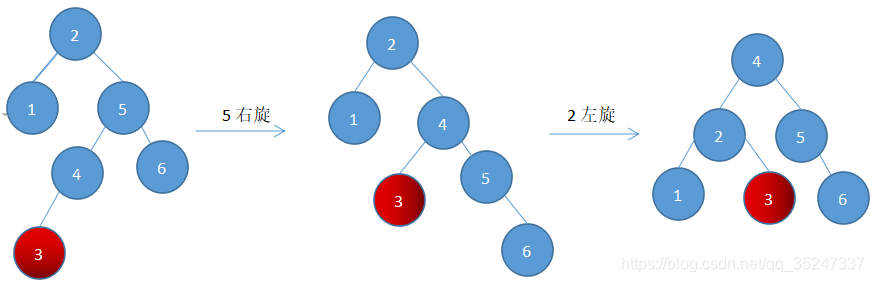
代码如下：

private Node RightLeftRotate(Node n1)
{
    n1.right = RightRotate(n1.right);
    return LeftRotate(n1);
}

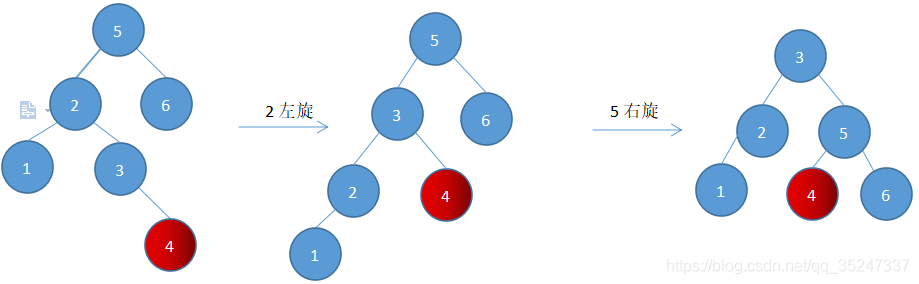
4)左右(先左后右)旋---在左节点的右子树插入新节点(左右插入 LR)

与上一种情况同理的，在左节点的右子树中插入新节点(注意，这里节点4不管在节点3的左节点还是右节点都是一样的)则先左旋后右旋

代码如下：

private Node LeftRightRotate(Node n1)
{
     n1.left = LeftRotate(n1.left);
     return RightRotate(n1);
}

最后，AVL树插入方法代码：

private Node Insert(Object item, Node n)
{    
    if (n == null)
         n = new Node(item, null, null);
    else if (((int)item).CompareTo((int)n.element) < 0)
    {
        n.left = Insert(item, n.left);
        if (GetHeight(n.left) - GetHeight(n.right) == 2)
        {
            if (((int)item).CompareTo((int)n.left.element) < 0)
                n = n.RightRotate(n);
            else
                n = n.LeftRightRotate(n);
        }       
    }
    else if (((int)item).CompareTo((int)n.element) > 0)
    {
        n.right = Insert(item, n.right);
        if (GetHeight(n.right) - GetHeight(n.left) == 2)
        {
            if (((int)item).CompareTo((int)n.right.element) > 0)
                n = LeftRotate(n);
            else
                n = RightLeftRotate(n);
        }
    }
    else
    { ;}// do nothing, duplicate value

    n.height = Math.Max(GetHeight(n.left), GetHeight(n.right)) + 1;
    return n;
}

删除

许多 AVL 树的实现会使用懒惰删除。这种方法会对要删除节点进行标记，但并不会真的把节点从树中删除掉。因为删除节点以及重新平衡树的执行开销常常使人望而却步.

非懒惰删除

这里说一下非懒惰删除，思路是删除左边不平衡时相当于在右边插入。

代码如下：

//找最小值
private Node FindMin(Node n)
{
    if(t != null)
    {
        return FindMin(n.left);
    }
    
    return null;
}

private Node Delete(Object item, Node cur，Node parant,bool isLeftChild)
{
    Node successor = null;
    if(cur == null)
        return null;
    else if(((int)item).CompareTo((int)cur.element) < 0)
    {
       cur.left = Delete(item,cur.left,cur,true);
       //执行到这里说明是从左边删除，相当于从右边插入，刚好与插入函数的逻辑进行了一个交换
       if (GetHeight(n.right) - GetHeight(n.left) == 2)
        {
            if (((int)item).CompareTo((int)n.right.element) > 0)//相当于RR插入
                n = LeftRotate(n);
            else//相当于RL插入
                n = RightLeftRotate(n);
        }
    }
    else if(((int)item).CompareTo((int)cur.element) > 0)
    {
       cur.right = Delete(item,cur.right,cur,false);
       //执行到这里说明是从右边删除，相当于从左边插入
       if (GetHeight(n.left) - GetHeight(n.right) == 2)
        {
            if (((int)item).CompareTo((int)n.left.element) < 0)//相当于LL插入
                n = n.RightRotate(n);
            else//相当于LR插入
                n = n.LeftRightRotate(n);
        } 
    }
    else if(cur.left!=null && cur.right!=null) //item==cur.element(cur为删除的节点)且有2个子节点
    {
        successor = FindMin(cur.right);//找后继节点
        cur.element = successor.element;
        cur.right = Delete(cur.element,cur.right,cur,false);
        cur.height = Max(GetHeight(cur.left), GetHeight(cur.right)) + 1;
    }
    else if(cur.left!=null)//cur为删除的节点且有1个右子节点
    {
        if(parent == null) //cur为根节点
            cur = cur.left
        else if(isLeftChild)
            parent.left = cur.left
        else
            parent.right = cur.left
    }
    else if(cur.right !=null)//cur为删除的节点且有1个左子节点
    {
        if(parent == null) //cur为根节点
            cur = cur.right
        else if(isLeftChild)
            parent.left = cur.right 
        else
            parent.right = cur.right 
    }
    else//cur为删除的节点且为叶子节点
    {
        if(parent == null) //cur为根节点
            cur = null
        else if(isLeftChild)
            parent.left = null
        else
            parent.right = null
    }

    return n
}