运动目标检测之背景建模（1）：混合高斯建模GMM的理解

参考链接1：GMM

运动物体检测的问题主要分为两类，摄像机固定和摄像机运动。

对于摄像机运动的运动物体检测问题，比较著名的解决方案是光流法 ，通过求解偏微分方程，求的图像序列的光流场 ，从而预测摄像机的运动状态。对于摄像机固定的情形，当然也可以用光流法，但是由于光流法的复杂性，往往难以实时的计算，所以可以采用背景模型法。因为，在摄像机固定的情况下，背景的变化是缓慢的，而且大都是光照，风等等的影响，通过对背景建模，对一幅给定图像分离前景和背景，一般来说，混合高斯建模是最常用。

找到研究方向以后，就是了解对应的算法。

1、单高斯模型和混合高斯模型
参考链接2：高斯模型

高斯模型有单高斯模型（SGM）和高斯混合模型（GMM）两种。

1.1单高斯模型

单高斯模型也就是我们平时说所的高斯分布(正态分布)，概率密度函数服从上面的正态分布的模型叫做单高斯模型，具体形式如下：

1.2 高斯混合模型（GMM）
高斯混合模型（GMM）是单高斯模型（SGM）的延伸，就是用多个高斯概率密度函数（正态分布曲线）精确地量化变量分布，是将变量分布分解为若干基于高斯概率密度函数（正态分布曲线）分布的统计模型。它可以平滑的近似任何形状的分布。反过来解释就是， K 个单高斯模型混合在一起，生成的模型，就是高斯混合模型。

GMM是工业界使用最多的一种聚类算法，每个单高斯模型可以看做是一个类别，通过计算样本属于各单高斯模型的概率来判断其最终的类别。它本身是一种概率式的聚类方法，假定所有的样本数据X由K 个混合多元高斯分布组合成的混合分布生成。

一般来说，一个混合模型可以使用任何概率分布，这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。

2、混合高斯背景建模理论和流程
参考链接：原理
参考链接3：理论

2.1 混合高斯背景建模理论
混合高斯背景建模是基于像素样本统计信息的背景表示方法，利用像素在较长时间内大量样本值的概率密度等统计信息(如模式数量、每个模式的均值和标准差)表示背景，然后使用统计差分(如3σ原则)进行目标像素判断，可以对复杂动态背景进行建模，计算量较大。
在混合高斯背景模型中，认为像素之间的颜色信息互不相关，对各像素点的处理都是相互独立的。对于视频图像中的每一个像素点，其值在序列图像中的变化可看作是不断产生像素值的随机过程，即用高斯分布来描述每个像素点的颜色呈现规律{单模态(单峰)，多模态(多峰)}。

对于多峰高斯分布模型，图像的每一个像素点按不同权值的多个高斯分布的叠加来建模，每种高斯分布对应一个可能产生像素点所呈现颜色的状态，各个高斯分布的权值和分布参数随时间更新。当处理彩色图像时，假定图像像素点R、G、B三色通道相互独立并具有相同的方差。对于随机变量X的观测数据集{x1,x2,…,xN}，xt=(rt,gt,bt)为t时刻像素的样本，则单个采样点xt其服从的混合高斯分布概率密度函数：

其中k为分布模式总数，η(xt,μi,t,τi,t)为t时刻第i个高斯分布，μi,t为其均值，τi,t为其协方差矩阵，δi,t为方差，I为三维单位矩阵，ωi,t为t时刻第i个高斯分布的权重。

2.2 混合高斯背景建模流程

1.每个新像素值Xt同当前K个模型按下式进行比较，直接找到匹配新像素值的分布模型，即同该模型的均值偏差在2.5σ内：

2.如果所匹配的模式符合背景要求，则该像素属于背景，否则属于前景。
3.各个模式权值按如下方式进行更新，其中a是学习速率，对于匹配的模式Mk,t=1,否则Mk,t=0，然后各模式的权重进行归一化：

4.未匹配模式的均值μ和标准差σ不变，匹配模式的参数按照如下更新：

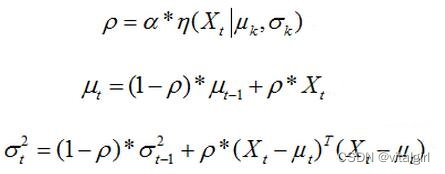
5.如果，第一步中没有任何模式匹配，则权重最小的模式被替换，即该模式的均值为当前像素值，标准差为初始较大值，权重为较小值。
6.各模式根据w/a^2按降序排列，权重大、标准差小的模式排列在前。
7.选前B个模式作为背景，B满足下式，参数T表示背景所占的比例：

<