机器学习——线性模型

一个离散属性的机器学习问题，转为分类或线性模型的关键就是怎么把这些离散值属性，如高矮，红绿用数值表现出来。通常来说，对于有序的属性，如{高、矮、胖}，我们可以用{1,0.5,0}表示。若属性中不存在有序关系，我们用向量来表示，如“西瓜”，“黄瓜”，“南瓜”可以转化为(1,0,0)，(0,1,0)，(0,0,1)。
线性模型
$$\begin{gathered} y_1=x_{11}{w}_1+x_{12}{w}_2+...+x_{1d}{w}_d \\ {y}_2=x_{21}{w}_1+x_{22}{w}_2+...+x_{2d}{w}_d \\ ..... \\ {y}_m=x_{m1}{w}_1+x_{m2}{w}_2+...+x_{md}{w}_d \end{gathered}$$

为便于分析，我们把b放到权向量里面。
$$w=[w_1,w_2,...,w_d,b]$$

$$y=[y_1,y_2,...,y_m]$$

$$\left(\begin{array}{ccccc}{x}_{11}& x_{12}& ...& x_{1d}& 1\\ x_{21}& x_{22}& ...& x_{2d}& 1\\ ...& ...& ...& ...& ...\\ x_{m1}& x_{m2}& ...& x_{md}& 1\end{array}\right)$$
注意：上面共有m个输入输出样本对，$(x_1,y_1),(x_2,y_2)...(x_m,y_m)$，每一组的输入有d个属性，如$(x_1,y_1)$，它的含义是输入为$(x_{11},x_{12}...x_{1d})$时，输出为y1，构建出的线性回归模型是d+1维。

矩阵形式可以表示为：
$$y=X{W}^T$$
若$X^{T}X$满秩，则易知$W^T=(X^{T}X{)}^{-1}{X}^{T}y$
广义线性模型：将线性模型利用非线性映射函数g(.)映射到非线性模型上去，以便更好地逼近。
$$y=g^{-1}(x^{T}w+b)$$
注意：g(.)线性可微

如对数线性回归：
$$lny=x^{T}w+b$$
对数几率回归（解决分类问题）
刚刚提出的线性模型可以解决回归问题，那么分类问题怎么解决呢？我们依旧可以构建一个线性模型，只是需要设置一个阈值，当$x^{T}w>C$，为1类等等。
常用对数几率函数解决二类分问题：
$$y=\frac{1}{1+e^{-z}}，z=x^{T}w+b.$$
上式可以转化为：
$$ln\frac{y}{1-y}=x^{T}w+b$$
其中$ln\frac{y}{1-y}$被称为对数几率，它反映了$x$作为正例的相对可能性。
线性判别分析（LDA ）
该方法就是利用投影的方法，将不同分类的样本点投影到一条直线上，从而使类内距离小，类间距离大，而使分类效果更好。

类内距离：$w^T{\Sigma }_{0}w+w^T{\Sigma }_{0}w$
类间距离：$\Vert w^T{\mu }_0+w^T{\mu }_1{\Vert }_2^2$
其中${\Sigma }_0$、${\Sigma }_1$为协方差矩阵。
类内散度矩阵($S_w$)
$$S_w={\Sigma }_0+{\Sigma }_1=\sum _{xϵX_i}(x-{\mu }_i)(x-{\mu }_i{)}^T,(i=0,1)$$

类间散度矩阵($S_b$)
$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$

准则函数J参考下式，J越大越好。

$$J=\frac{\Vert w^T{\mu }_0+w^T{\mu }_1{\Vert }_2^2}{w^T{\Sigma }_{0}w+w^T{\Sigma }_0}=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$$

多类分问题见西瓜书63页：

上述方法适合二类分，如果要进行多分类任务，我们引进全局散度矩阵。 **全局散度矩阵($S_{t}$):** $$ S_{t}=S_{b}+S_{w} $$

对于多类分问题，除了引进$S_t$外，$S_b$和$S_w$的计算方法也发生了改变，最后准则函数也会改变。
多分类学习
多分类学习的基本思路是拆解法，即将多个分类任务拆分成多个两类分任务。并为拆解出来的每一个两类分任务训练一个分类器，最后对分类器结果集成，得到多分类结果。
经典拆分策略：一对一（OvO），一对多（OvR），多对多（MvM）。
其中，OvO和OvR策略参考下图很容易清楚其思想内涵。

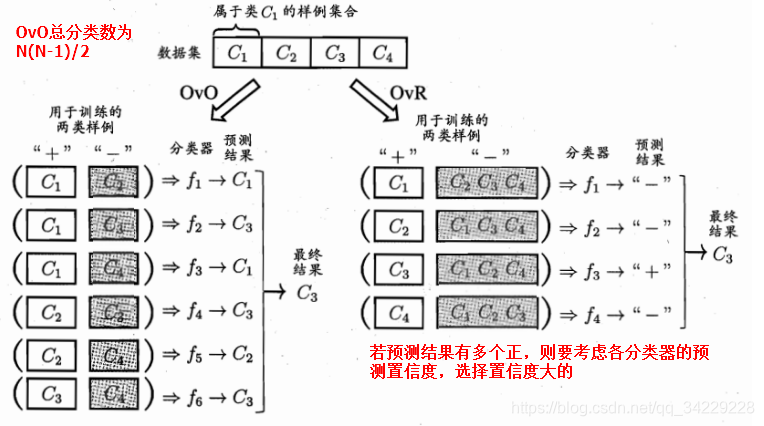
MvM: 就是M个分类器将N个类别做M次划分，每次有类别有一部分正例和一部分反例，如f1分类器将C2划分为正例，C1、C3、C4划分为反例。该方法包括编码和解码，编码就是f1要对类别以及测试示例进行编码。解码就是根据类别与测试样例距离最小找出测试样例最终属于哪一个类别。
常用MvM技术为纠错输出码ECOC。
该编码分为二元和三元，二元只将各类分为正类和反类，三元可以有停用类，即分类时不使用该类。

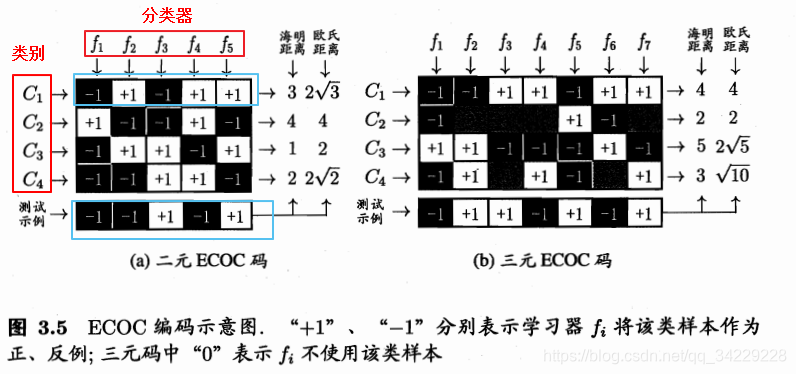
以蓝框C1和蓝框测试样例为例讲述明氏距离和欧氏距离的计算。
海明距：$0+1+1+1+0=3$
欧氏距离：$\sqrt{0+2^2+2^2+2^2+0}=2\sqrt{3}$
对于二元ECOC码，最后根据欧式距离最小应将它分为C3类。