计算理论导引-图灵机

最新推荐文章于 2024-04-12 01:35:55 发布

原创

最新推荐文章于 2024-04-12 01:35:55 发布 · 1.5k 阅读

7 ·

CC 4.0 BY-SA版权

本文深入探讨了图灵机的定义、与DFA的区别，并介绍了图灵机的格局表示、转换规则以及图灵机与确定性有穷自动机（DFA）的特性对比。进一步讨论了图灵可识别的、递归可枚举的和可判定的语言，以及它们之间的关系，包括通用图灵机和计算复杂性理论。最后，文章提到了计算历史、计算层次和一些重要的计算问题，如POST问题和EQTM问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

复习使用

定义

图灵机形式定义：
$m=(Q,\Sigma,\Gamma,\delta,q_{0},q_{accept},q_{reject})$
(1) $Q$ 是状态集
(2) $Σ\Sigma$ 编入定义表
(3) $Γ\Gamma$ 带定义表， $ε⊆Γ,⊔⊆Γ\varepsilon \subseteq \Gamma,\sqcup \subseteq\Gamma$
(4) $L,R}\delta:Q\times\Gamma\to Q \times \Gamma \times\{L,R\}$
(5) $q_0$ 为初态
(6) $q_{accept}$ 为接受状态
(7) $q_{reject}$ 为拒绝状态
格局
我们用格局表示图灵机的当前状态，当前带内容和读写头的当前位置的信息。
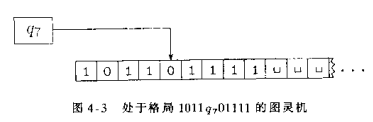
在这里插入图片描述
上图就是一种格局，我们表示为 $1011q_701111$ ，意思为：当前带内容是101101111，当前状态为 $q_7$ ，读写头当前在第二个0上。格局中状态后的第一个字符为读写头指向的位置。
如果图灵机能合法的从格局 $C_1$ 一步进入到 $C_2$ ，则称格局 $C_1$ 产生格局 $C_2$ ，可表示为 $C1→MC2C_1 \underset{M}{\rightarrow} C_2$ ，这个概念的形式定义如下：
设a,b和c是 $Γ\Gamma$ 中的符号，u和v是 $Γ∗\Gamma^{*}$ 中的字符串， $q_i$ 和 $q_j$ 是状态，则 $uaq_ibv$ 和 $uq_jacv$ 是两个格局。如果转移函数满足 $δ(qi,b)=(qj,c,L)\delta(q_i,b)=(q_j,c,L)$ ，则说：
$uaq_ibv$ 产生 $uq_jacv$
这说明了图灵机左移的情况，下面是右移的情况。如果 $δ(qi,b)=(qj,c,R)\delta(q_i,b)=(q_j,c,R)$ ，则说：
$uaq_ibv$ 产生 $uacq_jv$

图灵机与DFA的区别

DFA：确定性有穷自动机
1.带上可读写
2.读写头可左右移动
3.带子无限长
4.接受和拒绝状态都会停机

其他相关定义

如果 $w∈Σ∗∣∃u,v∈Γ∗,q0w→M∗uqacceptv}L(M)=\{w\in \Sigma^* |\exists u,v \in \Gamma^*,q_{0}w\xrightarrow[M]{*}uq_{accept}v\}$ 称 $w$ 是M接受（识别）的语言。
图灵可识别的/递归可枚举的( $r . e .$ )，定义为：
$L⊆Σ∗,r.e.⇔∃TMM(L=L(M))⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣→M∗uqacceptv))L\subseteq \Sigma^*,r.e.\Leftrightarrow \exists TM M(L=L(M))\Leftrightarrow\exists TM M\left ( \forall w \in L,\exists u,v \in \Gamma^*, \left ( q_0w |\xrightarrow[M]{*}uq_{accept}v\right )\right )$
图灵可判定的/图灵可递归的（recusive），定义为：
$L⊆Σ∗⇔∃TMM(∀w∈L,∃u,v∈Γ∗,(q0w∣→M∗uqacceptv)∧∀wˉ∉L,∃uˉ,vˉ∈Γ∗,(q0wˉ∣→M∗uˉqrejectvˉ))L\subseteq\Sigma^* \Leftrightarrow \exists TM M\left ( \forall w \in L,\exists u,v \in \Gamma^*, \left ( q_0w| \xrightarrow[M]{*}uq_{accept}v\right )\wedge\forall \bar{w} \notin L,\exists\bar{u},\bar{v} \in \Gamma^*, \left ( q_0\bar{w}| \xrightarrow[M]{*}\bar{u}q_{reject}\bar{v}\right ) \right )$
可递归的与可枚举的区别
1）可枚举的
在输入上运行TM时，可能达到停机状态，也可能达到循环即不停机状态
如果在，可达到这个状态，如果不在，没有回答
2）可判定的
对于任何输入，TM总能决定接受或者拒绝
如果在，可达到接受状态，如果不在，达到拒绝状态
可递归的与可枚举的联系
1）可判定的都是可识别的，可识别的不一定都是可判定的
2）设 $L⊆Σ∗,Lˉ=Σ∗−L,L is recusive， ⟺ L和Lˉ都是r.e.L\subseteq\Sigma^*,\bar{L}=\Sigma^*-L,L \, is \,recusive，\iff L和\bar{L}都是r.e.$
不是可识别的
$ATM‾、EQTM、EQTM‾、ETM\overline{A_{TM}}、EQ_{TM}、\overline{EQ_{TM}}、E_{TM}$
不是可递归的
$ATM、ATM‾、ETM、NETM、HALTTM、PCP、REGULARTMA_{TM}、\overline{A_{TM}}、E_{TM}、NE_{TM}、HALT_{TM}、PCP、REGULAR_{TM}$
通用图灵机：
$<M,w>∣TM M接受w}A_{TM}=\{<M,w>|TM \, M接受w\}$ ， $ATM is  r.e.(图灵可识别的)，ATM是不可判定的A_{TM} \,is\,\,r.e.(图灵可识别的)，A_{TM}是不可判定的$
构造 $\,U识别A_{TM}$