卡特兰数 大数求法 火车进站

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

火车进站题目链接

题目描述
一列火车n节车厢，依次编号为1,2,3,…,n。每节车厢有两种运动方式，进栈与出栈，问n节车厢出栈的可能排列方式有多少种。
输入描述:
一个数，n (n \leq 60000)n(n≤60000)
输出描述:
一个数s表示n节车厢出栈的可能排列方式
示例1

输入
3
输出
5

示例2
输入
50
输出
1978261657756160653623774456

ememmmm 这个证明卡特兰数怎么求呢？
参考闫学灿DALAO的B站视频


符合条件的入栈出栈序列都在y=x 这条线下面，一旦出现不合法的一定会在某一时刻经过y=x+1这条线。
什么叫符合条件：意思是一节车厢一定要先入栈在出栈不可能没入栈还出栈。所以拿x轴代表入栈 y轴代表出栈。符合条件的都是入栈数大于等于出栈数
并且， 一个符合条件的序列都可以找到一个对应的不合法序列在经过y=x+1之后且关于y=x+1对称（为什么不关于y=x轴对称？我也不太清楚，具体你要问问卡特兰）当对称之后入栈数为
n-1 出栈数为 n+1次
所以 公式来了，对于每节”车厢“都有两种操作可选，所以n节车厢有2n种选法，选了n次 减去不合法的次数 2n 中有n-1次

num = C（2n,n)-C(2n,n-1)= C(2n,n)/n+1;//注：C（2*n, n)意思是2n中选n个

所以这题就抽象为 求C（2n，n）/n+1

第一次尝试 暴力算

//时间复杂度达到 O（n^2)
#include <iostream>
#include <vector>

using namespace std;

int n, f[20];

vector<int> mul(vector<int> a, int b)
{
	vector<int> C;
	int k = a.size();
	int t = 0;
	for (int i = 0; i < k || t; i++)
	{
		if (i < k) t += a[i] * b;
		C.push_back(t % 10);
		t /= 10;
	}
	return C; 
}
vector<int> div(vector<int> a, int b)
{
	vector<int> c;
	int k = a.size();
	int r = 0;
	for (int i  = k-1; i >=0; i--)
	{
		r = r * 10 + a[i];
		//c[k-i] = r / b;
		c.push_back(r / b);
		r %= b;
	}
	reverse(c.begin(),c.end());
	while (c.size()>1 && c.back() == 0)c.pop_back();
	return c;
}
int main()
{
	ios::sync_with_stdio(false);
	vector<int>a,b;
	cin >> n;
	
	a.push_back(1);
	for (int i = 0; i < n; i++)
	{
		b = mul(a, 2 * n - i);
		
		a = div(b, i + 1);
		
	}
	a =div(a, n + 1);

	int k = a.size();
	for (int i = k-1; i >=0; i--)
		cout << a[i];
	system("pause");
	return 0;
}

超时了2333，所以需要优化.
那应该怎么优化呢？

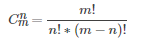
通过研究组合数的公式，我们不难发现
此题的数比较特殊
(2n-1)(2n-2)(2n-3)…(n+!).
——————————
(n-1)(n-2)(…)1
所以我们可以使用质因数分解（why？更快Y）将除法转变为乘法

统计组合数中素数的个数 用分子的个数 减去分母的个数 再将剩下的数乘起来 即得所求的数

Talk is cheap show me the code.

#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
const int N = 12010;
ll res[N],tt,q[N];
const int M = 1e9;
bool st[N];

void mul(int k)
{
	ll t = 0;
	for (int i = 0; i <= tt; i++)
	{
		res[i] = res[i] * k + t;
		t = res[i] / M;//这里做了压位处理 会更快一些（res一位可以存下一个亿的数）
		res[i] %= M;
	}

	while (t)
	{
		res[++tt] = t % M;
		t /= M;
	}
}

int get(int p, int b)//求p中b的个数
{
	int  s = 0;
	while (p)s += p / b, p /= b;
	return s;
}

void out()
{
	printf("%lld", res[tt]);
	for (int i = tt - 1; i >= 0; i--)
		printf("%09lld", res[i]);
	cout << endl;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 2; i <= n * 2; i++)
	{
		if (!st[i])
		{
			for (int j = i + i; j <= 2 * n; j+=i)
				st[j] = true;
		}
	}//线性筛素数

	for (int i = 2; i <= n * 2; i++)
	{
		if(!st[i])
		q[i] = get(2 * n, i) - get(n, i) * 2;
	}
	
	int k = n + 1;//因为这里要除以n+1，所以要减掉 n+1的质因数
	for (int i = 2; i <= k; i++)
		while (k%i == 0)
		{
			k /= i;
			q[i]--;
		}
	res[0] = 1;
	for(int i=2;i<=2*n;i++)
		while (q[i]--)
		{
			mul(i);
		}
	out();

	system("pause");
	return 0;
}