DFS试题集合

你有一个用于表示一片土地的整数矩阵land，该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小，返回值需要从小到大排序。

示例：

输入：
[
[0,2,1,0],
[0,1,0,1],
[1,1,0,1],
[0,1,0,1]
]
输出： [1,2,4]

int cnt=0;
    vector<int> pondSizes(vector<vector<int>>& land) {
         int row=land[0].size();
         int width=land.size();
         vector<int>ans;
         for(int i=0;i<width;i++)
          for(int j=0;j<row;j++)
          {
             if(land[i][j]!=0) continue;
            else 
            {
               dfs(i,j,land);
               if(cnt!=0)
               {
                ans.push_back(cnt);
                cnt=0;}
            }
          }
          sort(ans.begin(),ans.end());
          return ans;
    }
    void dfs(int i,int j,vector<vector<int>>& land)
    {
        int r=land[0].size();
        int w=land.size();
        if(i>=0&&j>=0&&i<w&&j<r)
           {
               if(land[i][j]==0)
               {
                   land[i][j]=-1;
                   cnt++;
               }
               else
                return;
           }
           else 
           return;
        dfs(i+1,j,land);
        dfs(i-1,j,land);
        dfs(i+1,j-1,land);
        dfs(i+1,j+1,land);
        dfs(i-1,j-1,land);
        dfs(i-1,j+1,land);
        dfs(i,j-1,land);
        dfs(i,j+1,land);
    }

回溯+深度搜索
请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如 [abcesfcsadee]\begin{bmatrix} a & b & c &e \ s & f & c & s \ a & d & e& e\ \end{bmatrix}\quad⎣⎡​asa​bfd​cce​ese​⎦⎤​ 矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

bool hasPath(char*matrix, int rows, int cols, char*str)
    {
         //bool visited1[cols*rows];
         vector<bool> visited(rows*cols,false);
         bool condition=false;
        for(int i=0;i<rows;i++)
            for(int j=0;j<cols;j++)
            {
               condition= (condition || dfs(matrix,i,j,rows,cols,str,visited));
            }
        return condition;    
    }
    bool dfs(char *m,int x,int y,int rows,int cols,char*c,vector<bool> visited)
    {
        if(x>=rows||y>=cols||x<0||y<0)//越界点
            return false;
        
        if(*c==m[x*cols+y]&&!visited[x*cols+y])
        {
            if(*(c+1)==0)//停止搜索的条件
                return true;
            visited[x*cols+y]=true;
            bool f=dfs(m,x+1,y,rows,cols,(c+1),visited)||dfs(m,x,y+1,rows,cols,(c+1),visited)||dfs(m,x,y-1,rows,cols,(c+1),visited)||dfs(m,x-1,y,rows,cols,(c+1),visited);
            //向四个方向出发
            if(!f)
              visited[x*cols+y]=false;//回溯@[TOC]@[TOC]((这里写自定义目录标题))
            return f;
               
        }
        else 
        {
            return false;
        }
        
    }
   

有一个二维矩阵 grid ，每个位置要么是陆地（记号为 0 ）要么是水域（记号为 1 ）。

我们从一块陆地出发，每次可以往上下左右 4 个方向相邻区域走，能走到的所有陆地区域，我们将其称为一座「岛屿」。

如果一座岛屿 完全 由水域包围，即陆地边缘上下左右所有相邻区域都是水域，那么我们将其称为 「封闭岛屿」。

请返回封闭岛屿的数目。

示例 1：

输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

class Solution {
public:
    //返回岛屿是否到达边界
    bool dfs(vector<vector<int>>& grid, int r, int c){
        if(r<0 || r>=grid.size() || c<0 || c>=grid[0].size()){
            return true; //是否到达边界，一次dfs搜索中只要有一个地方最终走到这儿就不是封闭岛屿了
        }

        if(grid[r][c]!=0){ //如果是海洋或是已经访问过的陆地则返回false，因为这两种情况不需要继续遍历，且也没找到边界
            return false;
        }

        //当前是陆地则继续
        grid[r][c] = 2; //标记为2表示已经访问过，也有人标记为海洋，但我觉得用一个独立的值更清晰些

        //四方向都要遍历到，不能因为某个方向找到边界就直接退出，因为这样找到的岛屿不完整，结果就错了
        bool res1 = dfs(grid, r-1, c);
        bool res2 = dfs(grid, r+1, c);
        bool res3 = dfs(grid, r, c-1);
        bool res4 = dfs(grid, r, c+1);
        return res1 || res2 || res3 || res4; //四方向遍历下去的结果，有任意一个方向接触边界就行
    }

    int closedIsland(vector<vector<int>>& grid) {
        int nr = grid.size();
        if(nr==0){
            return 0;
        }
        int nc = grid[0].size();
        int num = 0;

        for(int i=0; i<nr; ++i){
            for(int j=0; j<nc; ++j){
                if(grid[i][j]==0){  //岛屿题常规套路，找到一个陆地开始遍历
                    if(!dfs(grid,i,j)){ //如果dfs搜索完了发现这个岛不是接触边界，则封闭岛屿数增加
                        num++;
                    }
                }
            }
        }
        return num;
    }
};

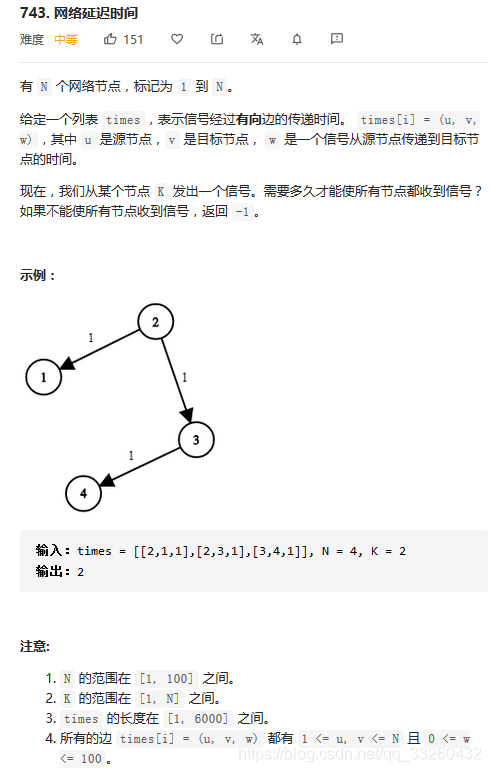
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
        const int INF = 0x3f3f3f3f;
        vector<vector<int>>graph(N+1, vector<int>(N+1, INF));//相当于N个节点，每个节点有N个输出节点(分别表示i到j的                                                  //长度)，第一个维度存放INF，下边有用；         
        for (vector<int> each : times) { 
            graph[each[0]][each[1]] = each[2]; //将times中的路径关系初始化到graph；
        }
        vector<int>dist(graph[K]); //将graph第K+1个元素作为dist，因为第一个用作默认值；
        vector<bool>st(N+1,false);//表示是否遍历过,记得赋初值
        st[K] = true;
        dist[K] = 0; //初始化->自己到自己的距离为0，且这个节点已经激活；
        for (int i = 0; i < N ; i++) {//这里是n-1，因为有N-1个节点没有激活；
            //找最短
            int t = 0;
            for (int i = 1; i <= N; i++) {//从1开始，到N，第0个就是为了放刚开始的t的；
                if (st[i] == false && (t ==0 || dist[i] < dist[t])) {
                    t = i;//更新最短路径
                }
            }
            st[t] = true; //将最小距离的索引处st设为true；
            for (int i = 1; i <= N; i++) {
                if (st[i] == false) { //遍历所有未激活的节点；
                    dist[i] = min(dist[i], dist[t] + graph[t][i]);
                }
            }
        }
        int ans = *max_element(dist.begin()+1, dist.end());//返回最大值
        return  ans == INF ? -1 : ans;

    }

void dfs(vector<int>& coins,int amount,int index,int count,int &ans)
    {
        if(amount==0)
          {
           ans=min(ans,count);
           return ;
          }
        if(coins.size()==index)
          return;
        for(int i=amount/coins[index];i>=0&&i+count<ans;i--)
        {
            dfs(coins,amount-i * coins[index],index+1,count+i,ans);
        }
    }
    int coinChange(vector<int>& coins, int amount) {
      sort(coins.rbegin(),coins.rend());
      int ans=INT_MAX;
      dfs(coins,amount,0,0,ans);
      //if(amount!=0)
        //return -1;
      //return ans;
      return ans == INT_MAX ? -1 : ans;
    }